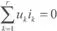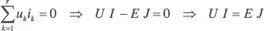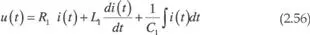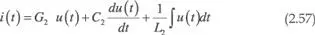Esta corriente (corriente equivalente de Norton) se corresponde con la corriente de cortocircuito obtenida en esos terminales, mientras que la resistencia (equivalente de Norton) se obtiene dividiendo la corriente de Norton por la tensión de vacío entre esos dos terminales.
Los equivalentes de Norton y de Thévenin son duales (véase el apartado 2.3.4).
• Teorema de Téllegen
Este teorema, consecuencia directa de las leyes de Kirchhoff, indica que:
Si un circuito eléctrico tiene r ramas, cada una de las cuales sometidas a la tensión uk y recorridas por la corriente ik, resulta que 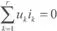
O dicho de otra forma, en todo circuito eléctrico la suma de las potencias generadas es igual a la suma de las potencias disipadas.
La figura E2.6.1 representa un convertidor continua-continua que enlaza una fuente de tensión E con una fuente de corriente I. Hallar la relación entre las magnitudes de entrada ( E , J ) y las de salida ( U, I ), supuesto el convertidor ideal.
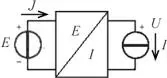
Figura E2.6.1
Solución
En aplicación del teorema de Téllegen, considerando el convertidor ideal, se puede escribir:
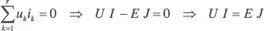
Véase, también, el ejercicio propuesto 2.8.7.
2.3.3. Concepto de recta de carga
Considérese el sistema de la figura 2.33.a, formado por un subsistema lineal, SL, y un resistor no lineal, RNL, por ejemplo, el resistor cuya característica estática, i = f ( u ), está representada en la figura 2.33.b
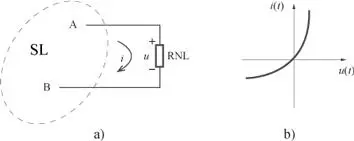
Figura 2.33. Resistor no lineal en un sistema lineal
Como se ha indicado en el apartado anterior, el subsistema de la figura 2.34.a, visto desde los puntos A y B, se puede sustituir por su equivalente de Thévenin, es decir, por una tensión equivalente en serie (U eq) con una resistencia equivalente ( R eq), resultando el circuito de la figura 2.34.a.
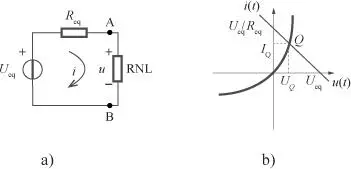
Figura 2.34. Recta de carga
Para resolver este circuito, bastará con escribir la ecuación de Kirchhoff de la malla resultante:

y resolver el sistema de ecuaciones:

Dado que se dispone del comportamiento del resistor no lineal representado en el plano ( u,i ), si se representa la expresión (2.54) en el mismo plano, la solución se encontrará en la intersección de ambas características. Como resulta evidente la ecuación (2.54) en el plano ( u,i ), es la recta que pasa por los puntos ( 0, U eq) y ( 0, U eq/ R eq), según se indica en la figura 2.34.b. Dicha solución Q ( u,i ) = ( U Q, I Q) es el denominado punto de trabajodel resistor RNL.
La ecuación (2.54) se denomina recta de cargade este circuito. De hecho la denominada recta de carga es un segmento de recta confinado en un cuadrante del plano ( i, u ), de puntos extremos la tensión de vacío, U eq, es decir la máxima tensión que se puede obtener entre los terminales A y B (figura 2.34.a) cuando éstos están abiertos, y la corriente de cortocircuito, U eq /R eq es decir la máxima corriente circulante cuando los terminales A y B están cortocircuitados.
Definición
Dos circuitos se dicen duales cuando constituyen dos representaciones físicas diferentes de un mismo sistema de ecuaciones diferenciales. Las ecuaciones de nodos de uno de los circuitos son las ecuaciones de mallas del otro, su dual.
Considérense los circuitos de la figura 2.35.
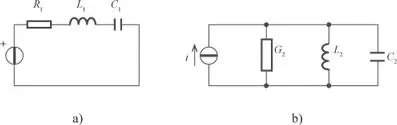
Figura 2.35. Circuitos duales.
La ecuación que caracteriza el circuito de la figura 2.35.a es:
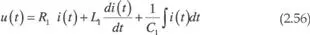
mientras que la ecuación que caracteriza el circuito de la figura 2.35.b es:
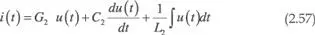
Se trata, efectivamente, de dos circuitos duales. Las dos ecuaciones (2.56) y (2.57) son la misma ecuación y, en consecuencia, tienen la misma solución. Se puede pasar de una a otra sin más que sustituir tensión por corriente, corriente por tensión, resistencia por conductancia, inductancia por capacitancia y capacitancia por inductancia. A los pares de elementos que se corresponden en dos circuitos duales se denominan elementos duales. En la tabla 2.4 se indica un conjunto de pares de elementos duales.
Tabla 2.4. Elementos duales.
| Tensión u |
Corriente i |
| Resistencia R |
Conductancia G |
| Inductancia L |
Capacitancia C |
| Fuente de tensión |
Fuente de corriente |
| Nodo |
Malla |
| Ley de Kirchhoff de tensiones |
Ley de Kirchhoff de corrientes |
| Equivalente de Thévenin |
Equivalente de Norton |
| Interruptor abierto |
Interruptor cerrado |
Búsqueda del circuito dual de un circuito dado
En primer lugar, debe indicarse que no a todo circuito dado le corresponde un circuito dual. Para ello, es necesario que el circuito del que se quiere hallar su dual sea un circuito representable en un plano, sin ramas imbricadas. Para hallar el circuito dual de un circuito dado se puede utilizar la técnica gráfica que se describe (véase la figura 2.36):
a)Poner un punto (nodo) en el centro de cada malla y un punto (nodo de referencia) en el exterior del circuito, que se corresponderá a la malla externa.
b)Dibujar tantas líneas, ramas duales entre dos nodos, como elementos haya en la rama común a las dos mallas en que se encuentran estos nodos. Ver figura 2.36.a.
c)Situar en cada rama dual el elemento dual del situado en la rama común a las dos mallas en el circuito inicial. Ver figura 2.36.b.
Читать дальше