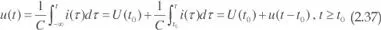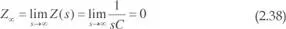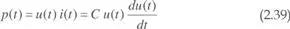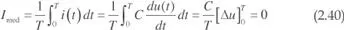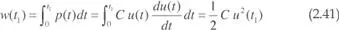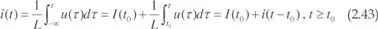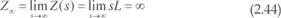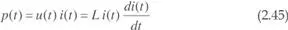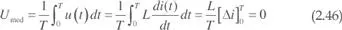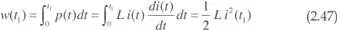Robert Piqué López - Electrónica de potencia

Como consecuencia de (2.36) resulta:

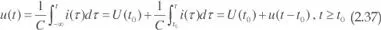
Esta expresión pone en evidencia que un condensador tiene el comportamiento de una fuente de tensión. En efecto, la tensión en bornes del mismo es una función integral que, por definición, es una función continua y, por tanto, cumple con la definición de fuente de tensión dada en el apartado 2.2.2. Efectivamente, su impedancia instantánea es nula:

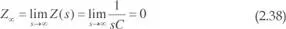
La potencia instantánea, teniendo en cuenta (2.27) y (2.36), resulta:

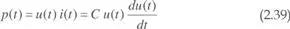
Con excitaciones periódicas y en régimen permanente el valor medio de la corriente en un condensador es nulo. Efectivamente, teniendo en cuenta (2.12) y (2.36):

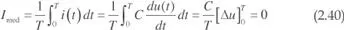
La energía eléctrica suministrada a un condensador durante el tiempo t 1, se acumula en un campo eléctrico y viene dada por:

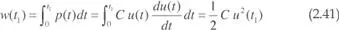
considerando que la energía en el instante inicial es nula.

Un inductor lineal e invariante temporal es un elemento circuital de dos polos cuya tensión en sus bornes es directamente proporcional a la derivada de la corriente que lo atraviesa. El coeficiente de proporcionalidad, L,se denomina inductancia propiadel inductor. Es decir:

En la figura 2.28 se indica su representación y el convenio de signos positivos que se adoptará en este libro.

Figura 2.28. Inductor.

La expresión (2.42) no se puede representar gráficamente en el plano ( u,i ), pero sí en el plano de fase ( u,di/dt ) como una recta de pendiente 1/ L (ver figura 2.29).

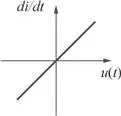
Figura 2.29. Inductor lineal e invariante temporal.

Como consecuencia de (2.42) resulta:

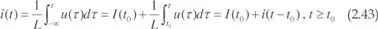
Esta expresión pone en evidencia que un inductor tiene el comportamiento de una fuente de corriente. En efecto, su tensión en bornes es una función integral que, por definición, es una función continua, por tanto, cumple con la definición de fuente de corriente dada en el apartado 2.2.2. Efectivamente, su impedancia instantánea es infinita

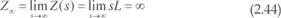
La potencia instantánea, teniendo en cuenta (2.27) y (2.42), resulta:

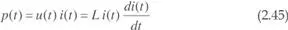
Con magnitudes periódicas y en régimen permanente, el valor medio de la tensión en un inductor en nulo. Efectivamente, teniendo en cuenta (2.12) y (2.42):

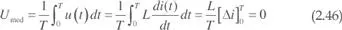
La energía eléctrica suministrada a un inductor durante el tiempo t1, se acumula en un campo magnético y viene dada por:

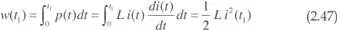
considerando que la energía en el instante inicial es nula.

Cuando dos inductores ( L 1y L 2) son atravesados por un flujo magnético común, se produce un acoplamiento magnéticoque da lugar a un fenómeno de inducción mutua que se caracteriza por la denominada inductancia mutua( L 12). En la figura 2.30 se muestran estos dos inductores como un elemento circuital de cuatro polos (tetrapolar), agrupados dos a dos.

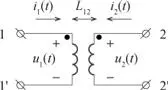
Figura 2.30. Inductancia mutua.

El comportamiento de este cuadripolo viene dado por el sistema de ecuaciones siguiente:

La corriente i 1( t ) que atraviesa el circuito primario (1-1’) induce por acoplamiento una tensión L 12 di 2( t )/ dt en el circuito secundario (2-2’). Esta tensión se añade algebraicamente a la tensión inducida en L 2por la corriente i 2( t ). Recíprocamente, i 2( t ) induce en el circuito primario una tensión L 12 di 2( t )/ dt que se añade algebraicamente a la tensión L 1 di 2( t )/ dt .

Se llama factor de acoplamientoa la magnitud:

Cuando k = 1, se dice que el acoplamiento es perfecto.

En función del circuito en el que esté emplazado este acoplamiento magnético, puede suceder que, en todo instante, sea nula o bien la corriente i 1( t ) o bien la corriente i 2( t ) (como ejemplo, ver apartado 4.5.1. Convertidor de retroceso ( flyback ). Por el contrario, puede suceder que, en todo instante, la presencia de una corriente i 1( t ) implique una corriente i 2( t ) diferente de cero (como ejemplo, ver apartado 4.5.2. Convertidor directo ( forward ). En este último caso, se dice que este acoplamiento magnético constituye un transformador.Se denomina transformador idealal transformador con factor de acoplamiento k = 1.

Considerando ideal el transformador de la figura 2.31, la aplicación de la tensión u (t) a las N1 espiras del primario da lugar a una variación de flujo magnético que íntegramente verán las N2 espiras del secundario. Por tanto se cumplirá: