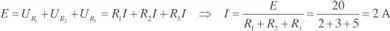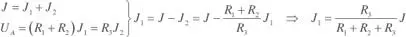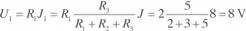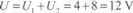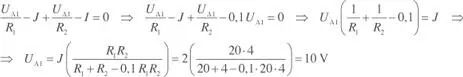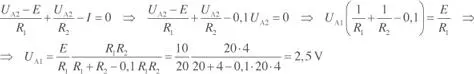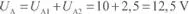Robert Piqué López - Electrónica de potencia

Considerando la superficie gaussiana SG 1, y al estar el sistema en vacío (corriente nula por la rama de e 0), debe cumplirse que i 1= i 2.

Segunda ley (de tensiones)

En la malla superior ( e 0- e 1- E 1) se cumple que E 1= e 1+ e 0. Así, se observa que si e 0crece hacia valores más positivos, e 1debe decrecer para mantener esta igualdad.

En la malla inferior ( e 0- e 2- E 2) se cumple que E 2= e 2- e 0. Así, se observa que si e 0decrece hacia valores negativos, e 2debe crecer hacia valores más positivos para mantener esta igualdad.

De la segunda ley de Kirchhoff así aplicada, se desprende que el máximo valor positivo para e 0es, precisamente E 1, obtenido cuando e 1= 0, mientras que su mínimo valor (el más negativo) es -E2, obtenido cuando e 2 = 0, de donde resulta que - E 2≤ e 0≤ + E 1.

Así, como consecuencia de esta forma peculiar de aplicar el principio de conservación de la energía, se desprende que la tensión de salida de un sistema electrónico está acotada por los límites que imponen sus tensiones de alimentación. A la diferencia entre las tensiones de alimentación, E 1- (- E 2) = E1 + E 2se le denomina máxima excursión de la tensión de salidadel sistema en cuestión, y si dicho sistema tiende a generar una tensión de salida que exceda a los límites impuestos por esta (- E 2≤ e 0≤ + E 1) se dice que el sistema está saturado.

• Principio de la superposición.

Es aplicable únicamente a circuitos lineales, como consecuencia de esa propiedad. Puede ser enunciado como sigue:

La respuesta de un circuito lineal a dos o más excitaciones, puede ser obtenida como superposición (suma) de las respuestas individuales del sistema dadas por cada una de las excitaciones cuando las otras no actúan.

Como aplicación del principio de la superposición considérese el circuito indicado en la figura E2.4.1 y calcúlese el valor de la tensión U en bornes de la resistencia R1, siendo: E = 20 V, J = 8 A, R 1= 2 Ω, R2 = 3 Ω, R3 = 5 Ω.

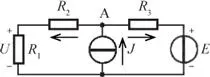
Figura E2.4.1

Solución

En primer lugar se calculará la tensión U 1en bornes de la resistencia R 1considerando únicamente la fuente de tensión E, dejando en circuito abierto la fuente de corriente J , según se indica en la figura E2.4.2.

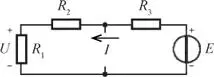
Figura E2.4.2

Aplicando la ley de Kirchhoff de tensiones resulta:

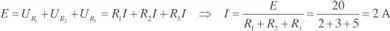
Por tanto: U1 = R1I = 2 · 2 = 4 V

A continuación se calculará la tensión U 2en bornes de la resistencia R 1considerando únicamente la fuente de corriente J , dejando en cortocircuito la fuente de tensión E , según se indica en la figura E2.4.3.

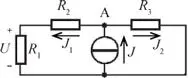
Figura E2.4.3

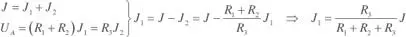
Por tanto: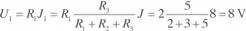

Y, en aplicación del principio de superposición:

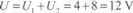
Como aplicación del principio de la superposición considérese el circuito indicado en la figura E2.5.1 y calcular el valor de la tensión U Aen el nodo A, siendo: E = 10 V, J = 2 A, I = 0,1 U A A, R = 20 Ω, R 2= 4 Ω.

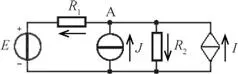
Figura E2.5.1

Solución

En este caso, en el circuito hay una fuente de corriente controlada por la tensión que debe siempre tenerse en cuenta sin alteración alguna.

Así, en primer lugar se calculará la tensión UA1 en el nodo A, considerando únicamente la fuente de corriente J , cortocircuitando la fuente de tensión E , según se indica en la figura E2.5.2. que cortocircuita.

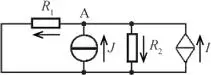
Figura E2.5.2

Si se aplica la ley de Kirchhoff de corrientes en el nodo A, resulta:

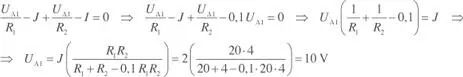
A continuación se calculará la tensión UA2 en el nodo A, considerando únicamente la fuente de tensión E , dejando en circuito abierto la fuente de corriente J , según se indica en la figura E2.5.3.

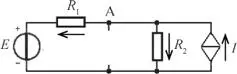
Figura E2.5.3

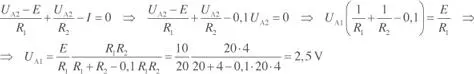
Así pues, la tensión U Asolicitada en el nodo A será:

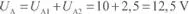
• Equivalente de Thévenin

Este teorema, aplicable únicamente a circuitos lineales, indica que:

Cualquier subcircuito eléctrico lineal, visto por dos terminales cualesquiera, es equivalente a una fuente de tensión en serie con una resistencia.

Esta tensión (tensión equivalente de Thévenin) se corresponde con la tensión de vacío obtenida en esos terminales, mientras que la resistencia (equivalente de Thévenin) se obtiene dividiendo la tensión de Thévenin por la corriente de cortocircuito entre esos dos terminales.

• Equivalente de Norton

Este teorema, aplicable únicamente a circuitos lineales, indica que:

Cualquier subcircuito eléctrico lineal, visto por dos terminales cualesquiera, es equivalente a una fuente de corriente en paralelo con una resistencia 3.