Scott D. Sudhoff - Power Magnetic Devices

Conversely, late in the evolution, suppose that individual B is slightly better than the rest of the population. Because the fitness of most individuals is quite good, the chances of individual B being put into the mating pool are not much more than that of an average individual. In this case, it is appropriate to scale the fitness of population member B so as to increase its likelihood of being put into the mating pool. Another purpose of scaling is that for roulette wheel selection, all fitness values need to be positive.

Many scaling algorithms take the form of (1.6-15). Therein, a and b are coefficients, which vary by algorithm, and f ′ denotes the scaled fitness. Expressions for a and b are listed by method in Table 1.4. In this table, f min, f max, f avg, and f meddenote the minimum, maximum, average, and median fitness of the population.

(1.6-15)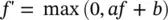

Another scaling method approach is quadratic scaling. In this algorithm, the scaled fitness is calculated as

(1.6-16)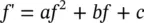

Table 1.4 Linear Scaling Methods

Method	a	b	Comments
Offset scaling	1	− f min	Ensures positive fitness
Standard linear scaling		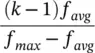f avg(1 − a )	Most fit individual k times more likely to be in mating pool than average
Modified linear scaling		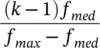f med(1 − a )	Most fit individual k times more likely to be in mating pool than median
Mapped linear scaling		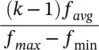− af min+ 1	Minimum fitness mapped to 1; maximum fitness to k
Sigma truncation	1	−( f avg− kf std)	Average fitness maps to kf std

where a , b , and c are given by

(1.6-17)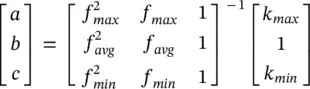

In (1.6-17), k maxand k minare algorithm constants selected such that k max> 1 and 0 < k min< 1. In this approach, an individual with a fitness equal to the population average is scaled to 1, the most fit individual has a scaled fitness of k max, and the least fit individual has a scaled fitness of k min. Thus, the most fit individual is k maxmore likely as an average fit individual to go into the mating pool, and the least fit individual is k mintimes more likely as the average fit individual to be put in the mating pool (which is less likely than average since k min< 1).

The point of a population‐based optimization is to search for the minimizer or maximizer using a large number of candidate solutions. Having large numbers of identical members of the population defeats the purpose of having a population in the first place. Diversity control algorithms examine the closeness of the solutions and compute a penalty for identical or nearly identical individuals; the penalized fitness is then used in the selection process.

In biological systems, there is no guarantee that the most fit individual in a population will survive long enough to procreate because of environmental influences. For example, the most fit grizzly bear in Alaska could be killed by a hunter. While examples of this occur every day in the natural world, as engineers we may not want to lose the best induction motor design in our population. This has led to the elitism operator. This operator compares the most fit individual in a new population to the most fit individual in the previous population. If the best fitness in the new population is lower than the previous population, the most fit member of the previous population replaces a member of the new population. In this way, the best fitness in the population cannot go down. While this operator is distinctly nonbiological, it normally results in improved algorithm performance.

In biological populations, it sometimes occurs that a population becomes geographically dispersed, and then members of these geographically isolated regions continue to evolve on separate evolutionary tracks. Sometimes, because of storms or random events, a few members of one region migrate into another region. These individuals then have children with members of the region which they have migrated into, often yielding very fit offspring.

It is possible to create GAs where such migration occurs. In such a GA, each individual is associated with a region, and for the most part, only individuals within a given region interact. Each region acts as a separate population. Occasionally, however, a few individuals are transferred between regions.

At first consideration, one might conclude that incorporating such behavior would have little effect on the algorithm. However, in Sudhoff [7] it is shown that at least in the case of one motor design example, the migration operator had a profound effect on the performance of the algorithm. That paper included a comparison between GA optimization and particle swarm optimization, and it found that choice of algorithm was less important than the use of migration in the GA or a somewhat analogous feature known as neighborhoods in particle swarm optimization.

In the canonical GA, the entire population is replaced by children. Those individuals who are selected in the mating pool but do not undergo any crossover, segregation, or mutation “survive” to the next generation unchanged. However, in some GAs, rather than forming a mating pool of the same size as the population, a mating pool that is a fraction of the size of the population is formed, thereby generating a population of children a fraction of the size of the population. The children replace members of the existing population, so that a new population is formed which has the children, plus some members of the previous population. In order to make room for the children (to hold the population size constant), it becomes necessary to decide which members of the current population will “die” to make room for the introduction of children. The selection of those individuals to be replaced can be made on criteria other than those used for selection—for example, based on diversity (or more particularly lack thereof) or some other attribute. In some sense, these approaches are reminiscent of biological populations, where the boundaries between generations are gradual.

After the initial generations of a GA, it is often the case that the most fit individuals are near a solution. In this case, some GAs will initiate local searches around the most fit individual. One way to accomplish this is to create a set of slight mutations of the most fit individual. Let us refer to the most fit individual as individual A, and refer to the population of mutations of this individual as P A. If the most fit individual in P Ais more fit than individual A, then the most fit individual of P Areplaces individual Α in the population.