Scott D. Sudhoff - Power Magnetic Devices
Здесь есть возможность читать онлайн «Scott D. Sudhoff - Power Magnetic Devices» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Power Magnetic Devices
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
- 80
- 1
- 2
- 3
- 4
- 5
Power Magnetic Devices: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Power Magnetic Devices»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Discover a cutting-edge discussion of the design process for power magnetic devices Power Magnetic Devices: A Multi-Objective Design Approach
Power Magnetic Devices
Power Magnetic Devices — читать онлайн ознакомительный отрывок
Ниже представлен текст книги, разбитый по страницам. Система сохранения места последней прочитанной страницы, позволяет с удобством читать онлайн бесплатно книгу «Power Magnetic Devices», без необходимости каждый раз заново искать на чём Вы остановились. Поставьте закладку, и сможете в любой момент перейти на страницу, на которой закончили чтение.
Интервал:
Закладка:
where N gis the number of genes in the chromosome in question. Both of these operators require gene repair.

Figure 1.12 Total mutation.
A final mutation operator we will consider is integer mutation. Recall that in integer coding, we are representing integers as real numbers and mapping them to a discrete set of values within [0,1]. In the case of integer‐coded genes, the mutation operators just described are not appropriate. Thus, it is convenient to use a total mutation of these genes with the result discretized to the allowed values.
The mutation operators just described all have uniform and nonuniform versions. In uniform versions, the parameters of the algorithms (the mutation rates, and standard deviations of mutation amount) are constant with respect to generation number. In nonuniform mutation, these rates vary. Normally, high mutation rates and large standard deviations are used at the beginning of evolution while smaller rates and standard deviations are used toward the end of the study when the population is mature from an evolutionary point of view.
Example 1.6A
Let us illustrate the use of an elementary GA based on a real‐coded version of Figure 1.8. In particular, let us attempt to find the value of xthat maximizes the function
(1.6A-1) 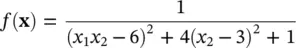
For the purposes of solving this problem, we will use linear coding with x mn,1= x mn,2= 0 and x mx, 1= x mx, 2= 5. In order to form the mating pool, we will use two‐way tournament selection. We will also assume simple‐blend crossover with α = 0.5 and a probability of crossover of 0.5. We will use total mutation with the probability of a gene mutation of 0.1. In this example, we will consider three generations with a population size of 8. The code for this example can be obtained from Sudhoff [6].
Table 1.3lists the data for the evolution. The first population’s parameters were determined by random initialization. Next, the parameter vector for each member of the population was decoded yielding x ifor every member of the population. This is then evaluated by calculating f i= f( x i), where the fitness is given by (1.6A-1). At this point, the maximum, median, and mean fitness values of the population are 0.2213, 0.04123, and 0.06940, respectively. The next step is the creation of the mating pool using tournament selection. Applying simple‐blend crossover, mutation, and associated gene repair operators yields the second population. Decoding to obtain the parameter vector for each element and then evaluating the fitness, it can be seen that maximum and mean fitness values of the population have increased to 0.4886 and 0.09160 while the median fitness is decreased to 0.03661. Repeating the process a third time, the maximum, median, and mean fitness increase to 0.7719, 0.08486, and 0.1774, respectively. After the third generation, taking the individual with the highest fitness yields x *= [1.942 3.233] T. This is starting to approach the correct solution, which is x = [2 3] T. Note, however, that a different run will produce different results since a population size of 8 over three generations is inadequate to find a consistent solution.
Before concluding this example, it is interesting to repeat it with a more substantial population size and over a larger number of generations. Figure 1.13illustrates an optimization run over eight generations with a population size of 25 individuals. In Figure 1.13(a), the best fitness in the population, median fitness of the population, and mean fitness of the population are shown versus generation. All three of these quantities can be seen to increase with generation number, though not monotonically. Figure 1.13(b) depicts a plot of the individuals in terms of their parameter vectors. Therein, an o, x, +, *, star, diamond, triangle, and pentagram depict members of the first through eighth generations, respectively. In addition, the darkness of the shading of each point is proportional to generation number. Thus, it can be seen that as the evolution progresses, the population moves toward the objective function maximizer. At the end of the run, the estimate of the solution is x *= [2.133 2.755] T, which yields f( x *) = 0.797. With the given limited number of generations and small population size, the results vary from run to run. This variance could be eliminated with a larger population and more generations, but it would make the resulting figures (particularly Figure 1.13(b)) hard to trace.
Table 1.3 Example of Real‐Coded Genetic Algorithm Evolution
| Generation 1 | ||||||||
| P[1] | 0.32100.8296 | 0.82220.5707 | 0.57180.2860 | 0.69910.7963 | 0.44160.4462 | 0.46570.2790 | 0.67540.9037 | 0.90850.7472 |
| x i | 1.60514.1478 | 4.11092.8534 | 2.85911.4301 | 3.49573.9813 | 2.20792.2311 | 2.32831.3952 | 3.37694.5183 | 4.54263.7360 |
| f i | 0.1492 | 0.0295 | 0.0689 | 0.0148 | 0.2213 | 0.0530 | 0.0104 | 0.0081 |
| M[1] | 0.57180.2860 | 0.46570.2790 | 0.82220.5707 | 0.32100.8296 | 0.46570.2790 | 0.82220.5707 | 0.44160.4462 | 0.32100.8296 |
| Generation 2 | ||||||||
| P[2] | 0.57180.2860 | 0.13550.3321 | 0.89750.7424 | 0.65340.6579 | 0.46570.2790 | 0.52790.0321 | 0.36270.6971 | 0.84670.5786 |
| x i | 2.85911.4301 | 0.67741.6606 | 4.48743.7118 | 3.26683.2895 | 2.32831.3952 | 2.63940.1604 | 1.81333.4857 | 4.23362.8932 |
| f i | 0.0689 | 0.0313 | 0.0086 | 0.0419 | 0.0530 | 0.0155 | 0.4886 | 0.0249 |
| M[2] | 0.13550.3321 | 0.57180.2860 | 0.36270.6971 | 0.57180.2860 | 0.84670.5786 | 0.84670.5786 | 0.57180.2860 | 0.65340.6579 |
| Generation 3 | ||||||||
| P[3] | 0.13550.3321 | 0.57180.2860 | 0.54620.3365 | 0.38830.6467 | 0.84670.5786 | 0.84670.5786 | 0.62350.5216 | 0.60170.4223 |
| x i | 0.67741.6606 | 2.85911.4301 | 2.73081.6824 | 1.94173.2334 | 4.23362.8932 | 4.23362.8932 | 3.11742.6082 | 3.00852.1114 |
| f i | 0.0313 | 0.0689 | 0.1008 | 0.7719 | 0.0249 | 0.0249 | 0.1625 | 0.2335 |
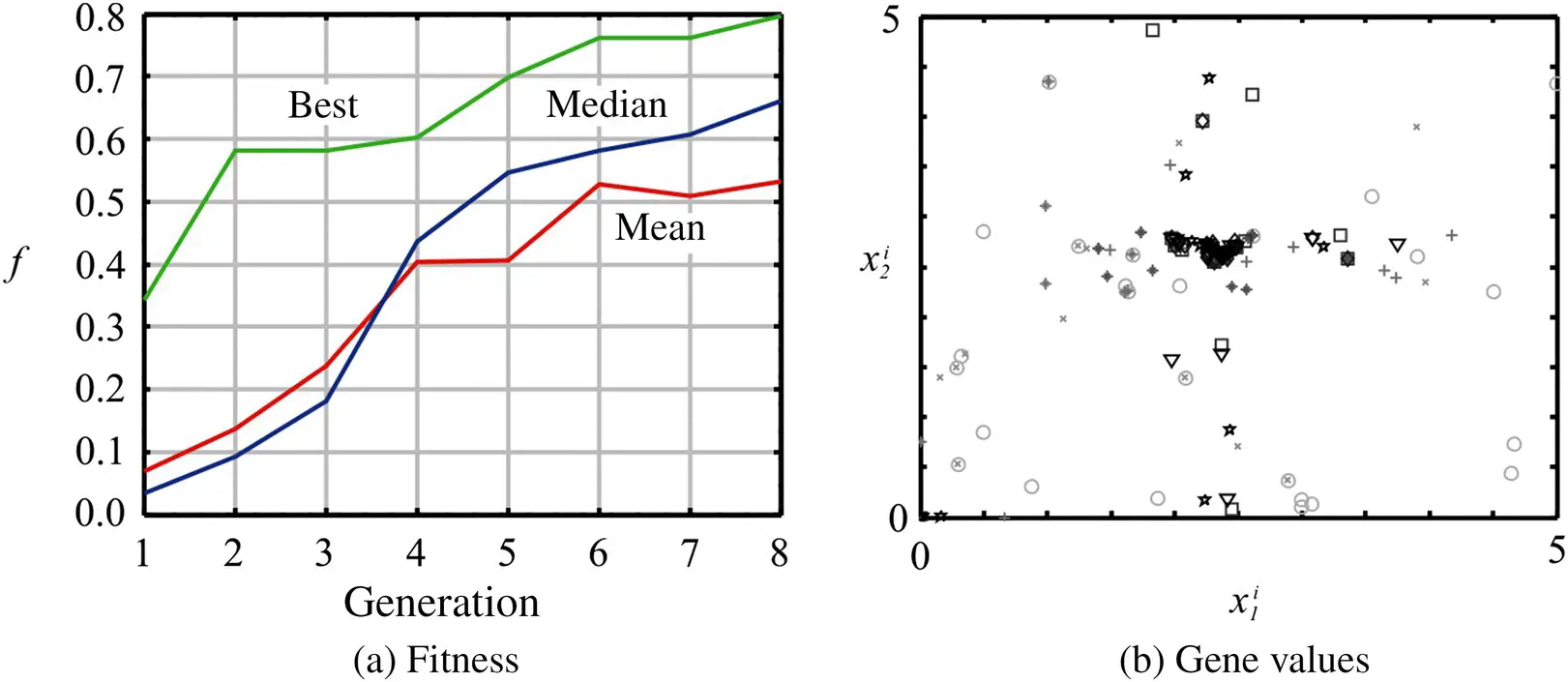
Figure 1.13 Fitness and gene values for Example 1.6A.
While Example 1.6Ahelped to illustrate the operation of a real‐coded GA, practical GAs typically have several additional features to increase their efficacy. We will now briefly consider some of these additional operators.
Scaling
Scaling the fitness values of a population can result in improved algorithm performance. Scaling algorithms are only used in the context of roulette wheel selection. Consider a situation early in an evolution. Suppose individual A is significantly more fit than the remainder of the population. In this case, many copies of individual A will become part of the mating pool. In fact, without scaling, copies of individual A can rapidly dominate the population, leading to premature convergence and a failure to fully explore the search space. In this case, the scaling algorithm could be used to reduce the fitness of individual A so that it does not become as common as quickly, permitting the evolution to explore other avenues.
Читать дальшеИнтервал:
Закладка:
Похожие книги на «Power Magnetic Devices»
Представляем Вашему вниманию похожие книги на «Power Magnetic Devices» списком для выбора. Мы отобрали схожую по названию и смыслу литературу в надежде предоставить читателям больше вариантов отыскать новые, интересные, ещё непрочитанные произведения.
Обсуждение, отзывы о книге «Power Magnetic Devices» и просто собственные мнения читателей. Оставьте ваши комментарии, напишите, что Вы думаете о произведении, его смысле или главных героях. Укажите что конкретно понравилось, а что нет, и почему Вы так считаете.












