Scott D. Sudhoff - Power Magnetic Devices

Suppose the 13th member of the population has the genetic code

(1.5A-1)

The decoding algorithm is on a gene‐by‐gene basis and is of the form

(1.5A-2)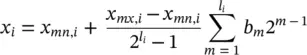

where l iis the number of bits of the i th gene, m is an index ranging from least significant (rightmost) bit to most significant (leftmost) bit for a given gene, b mis the value of that bit (0 or 1), and x mn,iand x mx,iare the minimum and maximum values of the i th element of the parameter vector. For the problem at hand, we assume x mn,1= 5, x mx,1= 10, x mn,2= − 2, x mx,2= 0, x mn,3= 0, and x mx,3= 1. In Section 1.9, we will formally consider the construction of fitness functions, and in Section 1.10, we will consider an engineering example. However, for the moment we will assume a purely mathematical fitness function given by

(1.5A-3)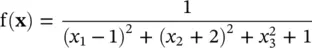

Our goal is to compute the fitness of the 13th member of the population.

The solution to this problem is straightforward. Using (1.5A-2), we obtain 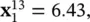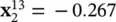, and 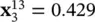. Substitution of these values into (1.5A-3)yields f 13= 0.0297. Note that while the division of the bits of (1.5A-1)into genes is very important to determine the fitness, the organization of genes into chromosomes is irrelevant for fitness evaluation and so has not been specified in this example.

At this point, we can now consider the primary aspects of a GA. These are illustrated in Figure 1.8. Therein, the first step is initialization that yields an initial population denoted P[1]. Next, the fitness of every member of the population is evaluated. Based on the fitness, a mating pool M[ k ] is determined by the selection process. The individuals in this population will mate and genetic operators such as crossover, segregation, and mutation will be used to produce children who will form the next generation P[ k + 1]. A stopping criterion is then checked; this can be as simple as checking a generation number. Once the stopping criterion is met, the algorithm concludes by selection of the most fit individual of the final population to be the optimizer. This process is implemented by the argmax() operator, which returns the argument that maximizes its objective (which, in this case, is carried about by inspection of the finite population).

It is now appropriate to consider each of these operations in more detail, beginning with the initialization step. The genetic code of every member of the population is initialized at random. This yields an initial population of designs, denoted P[1]. The next step in the algorithm is to compute the fitness of every member of the population. This is accomplished by applying (1.5-3)and (1.5-5)to every member of the population. Example 1.5Aillustrates this step for a single member of the population.

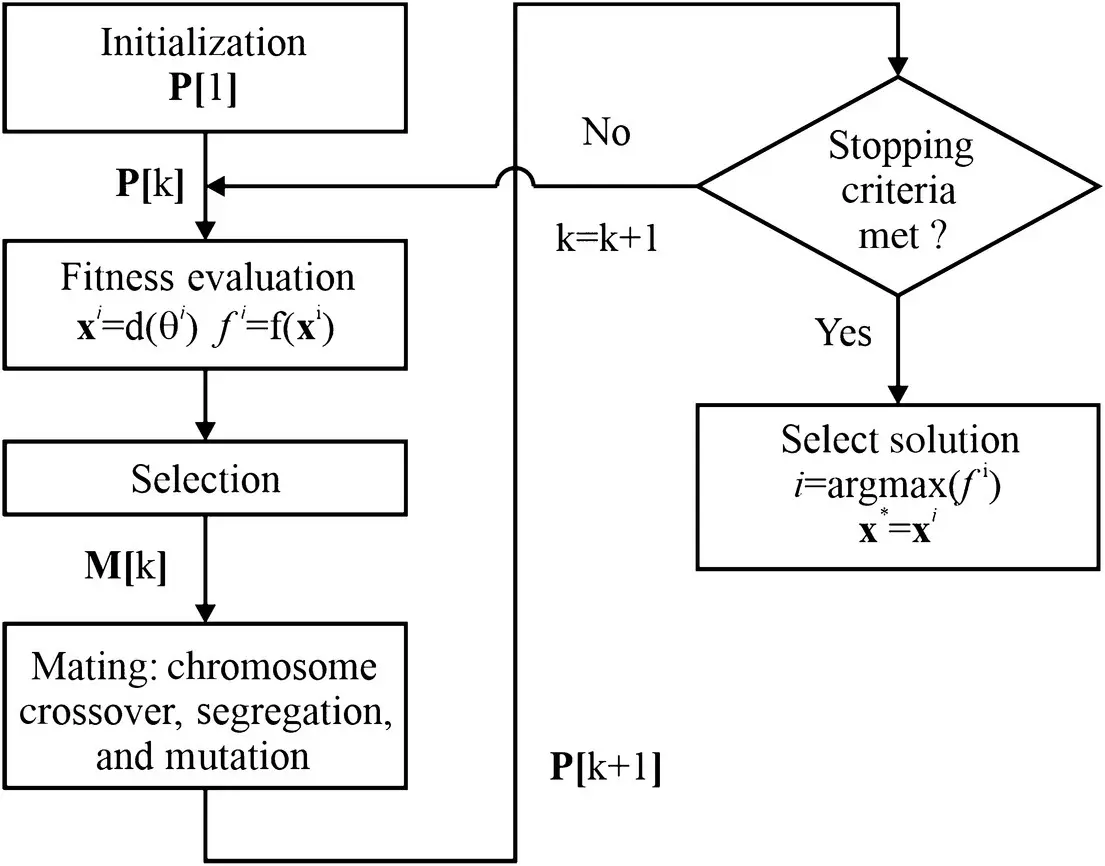
Figure 1.8 Canonical genetic algorithm.

The next step in the process is selection. In this step, members of the population P[ k ] are placed into the mating pool M[ k ]. Two algorithms to do this are roulette wheel selection and tournament selection. In both methods, the mating pool is initially empty and is filled one member at a time by repeatedly applying the selection mechanism. In roulette wheel selection, members of the population are drawn into the mating pool with a probability proportional to their fitness. In particular, the probability of individual i being drawn into the mating pool on a given draw is given by

(1.5-6)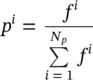

When applying this particular algorithm, it is important that the fitness function be constructed so that f i≥ 0. If this is not the case, it is possible to scale/adjust the fitness so that the condition is satisfied (for example, by adding a constant). Note that once a population member has been copied to the mating pool, it is not removed from the population. Thus, it can be copied to the mating pool multiple times.

In n ‐way tournament selection, n members of the population are selected at random, and the member of this subset with the highest function is put into the mating pool. Here again, the member placed into the mating pool is not removed from the population. In tournament selection, there is no restriction on the range of the fitness function, which provides a slight simplification.

The next step in process is mating, which is comprised of chromosome crossover, segregation, and mutation. In this step, pairs of parents are used to create pairs of children. Pseudo‐code for this step appears in Table 1.2. Therein, underlined text denotes comments. Referring to the pseudo‐code, θ p1and θ p2denote the genetic code from parents taken from the mating pool. A crossover operator is applied to the codes to form intermediate genetic codes θ a1and θ a2. Crossover occurs at random points within a given chromosome. If it occurs, then all elements of the portion of the chromosome strings of the two parents past the crossover point are interchanged. This is similar to biological crossover but not identical: In the case of biological crossover, this process occurs in the formation of the gametes. The net result is the same. Next, the chromosomes of θ a1and θ a2are randomly segregated to form the next stage of intermediate codes θ b1and θ b2, much as the chromosome pairs of a cell are segregated in forming gametes. Genetic codes θ b1and θ b2are then mutated to form θ c1and θ c2, which will be the children. The mutation operator consists of random interchanges of 0 and 1. The final step in the process is that the children θ c1and θ c2are placed into the next generation P[ k + 1]. It should be noted that in many GAs there is only a provision to have one chromosome, in which case the chromosome segregation process does not come into play and so genetic diversity is brought about solely by crossover and mutation.

Table 1.2 Pseudo‐Code for Mating, Crossover, Segregation, and Mutation