Scott D. Sudhoff - Power Magnetic Devices

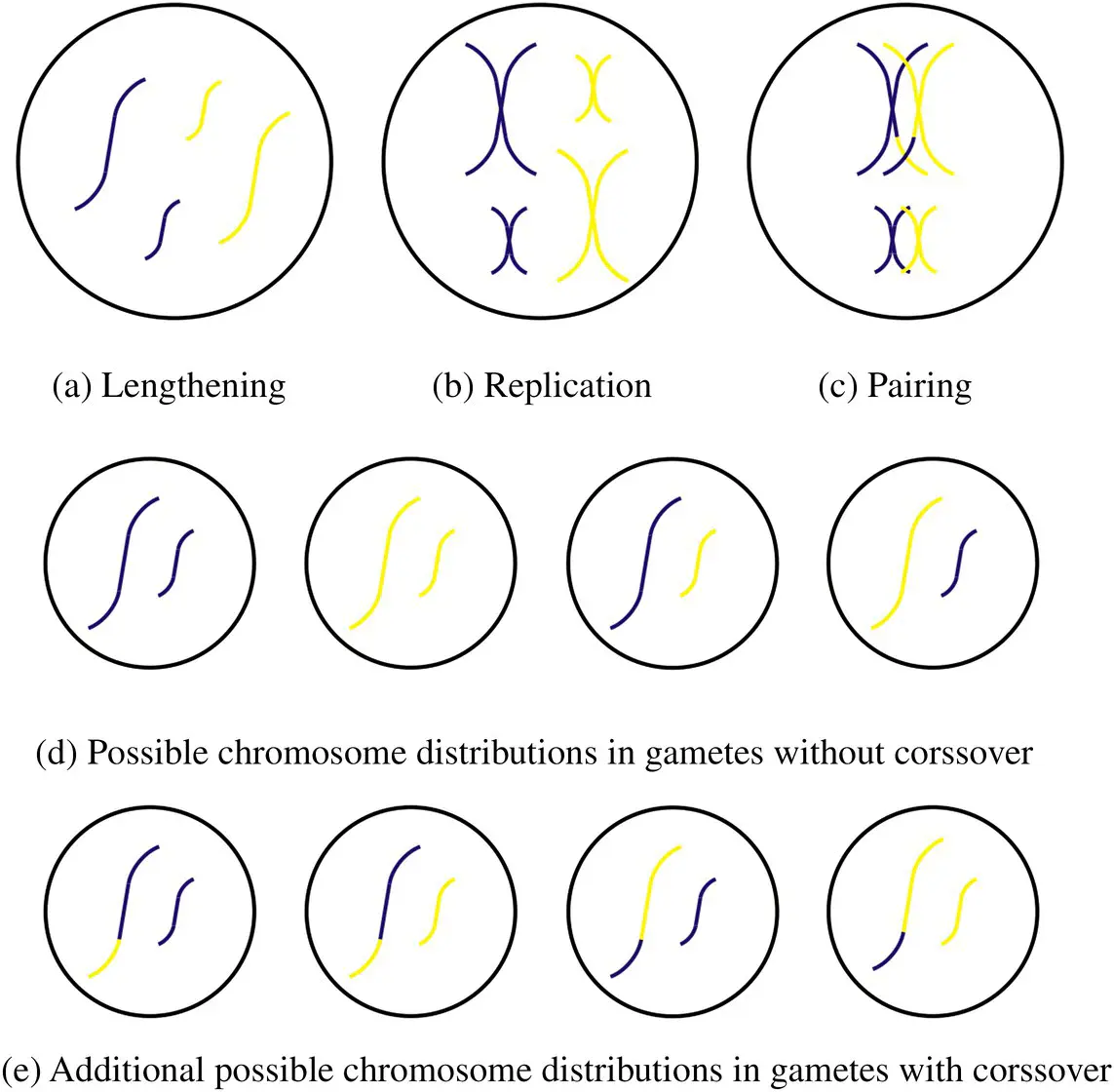
Figure 1.7 Meiosis.

After the chromosome pairing and crossover, the cell, which now contains four versions of each chromosome, splits into four cells. The four chromosomes segregate into these four cells. If crossover did not occur, this two‐chromosome organism could produce four genotypes (genetically unique) of gametes; therefore, a single mother–father pair could produce sixteen genotypes. However, because of the crossover, many additional genotypes of gametes can be produced. In fact, because of crossover, the number of genotypes that can be produced becomes related to the number of genes, not just the number of chromosomes. Thus, crossover is very important in achieving genetic diversity.

Of course, in the case of humans, chromosome distribution alone with 23 pairs of chromosomes, yields 2 23= 8,388,608 genotypes for the gametes. A set of parents could thus produce 8,388,608 2genetically different children, which would seem to be an impressively diverse set, even without crossover. However, in artificial GAs, the number of chromosomes is much smaller, often consisting of a single chromosome.

Beyond increasing the sheer number of genotypes of the gametes, crossover plays another critical role because it allows beneficial genes (traits) on a given chromosome to be decoupled from detrimental genes (traits). Crossover will play a very important role in the operation of GAs.

In addition to gamete diversity due to genetic crossover and chromosomal segregation into gametes, additional diversity is brought about because of mutation. Mutation arises from errors in copying DNA. In mitosis, or cell division, mutation often has little effect, since the mutated cell will often die. However, in meiosis, mutation can have a significant impact since the mutated genetic code will propagate into the genetic code of every cell in the child. Even then, many mutations are not noticeable because they are a part of the genetic code that is unused. When mutation has a noticeable effect, it is generally for the worse. However, occasionally beneficial mutations occur which improve the ability of an individual (and eventually a species) to survive.

A final concept from biology that will serve our needs for an optimization engine is the idea of natural selection and the survival of the fittest, an idea stemming from Charles Darwin’s voyages of the H.M.S Beagle, during a period of time roughly contemporary with the work of Mendel and the American Civil War. The idea that the most fit individuals of a population survive to reproduce is directly used in GAs. These algorithms are based on an explicit fitness function, which will be used to determine which individuals “survive” and will be placed into a mating pool.

Clearly, the discussion in this section is at a high level and has been greatly simplified. The interested reader is referred to Crow [2] for a more thorough introduction to the topic.

A century after the work of Mendel and Darwin, but a mere decade after the work of Watson and Crick, John Holland, a professor at the University of Michigan, proposed using the principles of biological genetics as a computation algorithm for optimization, a concept instantiated by a GA [3]. In this section, we will begin our consideration of GAs with a canonical GA similar to Holland’s original vision.

GAs are quite different from traditional optimization algorithms. First of all, GAs operate not on the argument of the function being optimized, but rather on an encoding of the argument. Second, rather than iterating to improve an estimate for an optimizer, GAs iterate to improve a large number of different estimates of the optimizer. This collection of estimates will be referred to as a population. The use of a population of estimated solutions improves the chances of finding a global optimum. Third, GA operations are based only on the values of the objective function—gradients and Hessians are not used, nor even estimated. This property is useful in function with discontinuities or with a discrete or mixed search space. Finally, GA operations are based on probabilistic rather than deterministic computations.

The first concept that must be set forth in a GA is that it, like evolution, operates on a population, not on an individual. We will denote the population within the GA as P[ k ], where k is the generation number. The k th generation consists of a number of individuals, that is,

(1.5-1)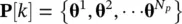

where θ iis the genetic code for the i th individual in the k th generation of the population and where N pdenotes the number of individuals in the population, which should be an even number. The genetic code for the i th individual may be organized as

(1.5-2)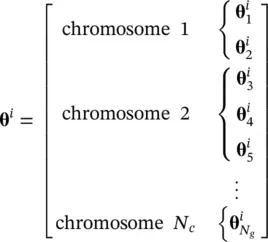

where N cis the number of chromosomes, N gis the number of genes, and 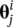is the j th gene of the i th individual (and it is understood that we are referring to the k th generation). Each gene is a string sequence. Recall that DNA consists of alphabet AT, TA, CG, and GC. In the case of the canonical GA, the string is most typically a binary sequence. Thus, θ itakes the form of a binary number. The significance of the chromosome organization will come into play when we consider reproduction.

The fact that the genes are encoded results in a limitation of the domain of the parameter vector. In other words, the domain of possible values of each element of the parameter vector is inherently limited. In some cases, this property is very convenient, but in other cases this limitation on the domain of the parameter vectors is disadvantageous.

Associated with the genetic code for each population member, we will have a decoding function that translates the genetic code into a parameter vector. In particular,

(1.5-3)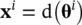

where x iis the parameter vector of the i th member of the population and is structured as

(1.5-4)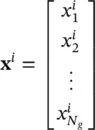

As can be seen, x ihas one element (denoted with a subscript) for each gene. However, it is not partitioned into chromosomes.

Based on the parameter vector of i th population member, the objective function can be evaluated. In particular,

(1.5-5)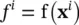

In the case of a GA, the objective function is referred to as a fitness function. It will be used in a “survival of the fittest” sense to determine which members of the population will mate to form the next generation. In the context of a GA, fitness is viewed in a positive sense, thus it is assumed that we wish to maximize the fitness function. Fortunately, it is a straightforward matter to convert between maximization of a function and the minimization of a function. At this point, we have enough background to discuss the computational aspects of a GA. However, before doing this, it is appropriate to briefly pause in our development and consider an example.