Scott D. Sudhoff - Power Magnetic Devices

The manual design process we have been considering involves an engineer in the iteration process. Variations of this process are successfully used ubiquitously throughout the engineering community. However, the process has some significant drawbacks. First, it requires a great deal of engineering time. Second, it requires a great deal of engineering experience. This experience comes into play in the development of the design equations, which often take the form of rules‐of‐thumb based at least partially on experience. Experience is also a factor in making changes to the design based on the numerical analysis. Finally, while the process has been very successful in yielding working designs, it may not lead to the best design.

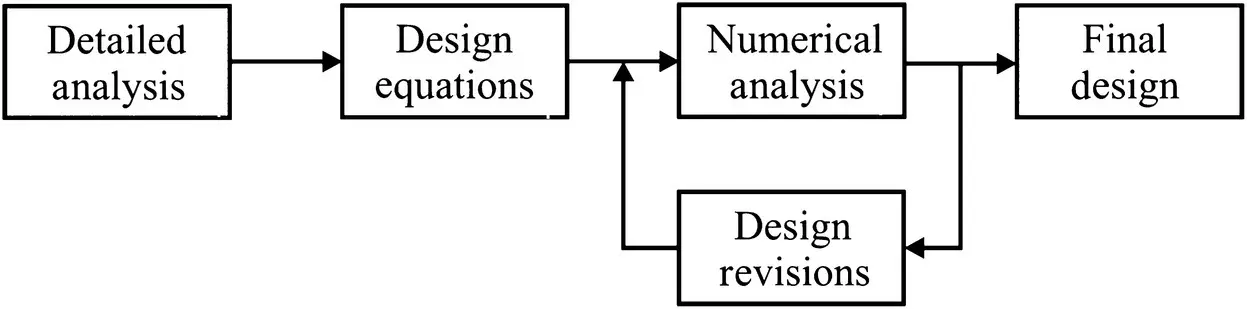
Figure 1.1 A manual design process.

Figure 1.2 Optimization‐based design process.

An alternate design process is illustrated in Figure 1.2. Therein, an optimization‐based design process is shown. In this case, the process is not illustrated in a sequential manner as in Figure 1.1, but rather in an organizational manner. The process again starts with a detailed analysis of the device or component. However, unlike the manual design process, in the optimization‐based process, the detailed analysis is not used to formulate design equations. Instead, the detailed analysis is used to calculate design metrics such as mass, cost, and loss. The detailed analysis is also used to check constraints such as achieving some minimum acceptable level of performance. The metrics and constraints are combined into an objective or fitness function. This function is defined so that its optimization results in optimization of the design metrics subject to all design constraints being met.

At the outermost level of this design process, an optimization engine will select the parameters of the design (geometry, materials, etc.) so as to maximize the objective function. In terms of computational algorithm, Figure 1.2depicts an optimization engine at the outer level. This engine operates on an objective function that is calculated based on the detailed analysis.

There are several advantages of this approach. First, it is unnecessary to formulate design equations. This is beneficial in that it reduces the number of approximations and assumptions made and reduces the amount of design experience needed for a good design. Second, the design is formally optimized with regard to the design metrics, potentially leading to better designs, at least in terms of the design metrics. Third, since the engineer is out of the optimization loop, less engineering time is generally required. There are some disadvantages of the procedure. First, the process can be numerically intense and require significant computing time, sometimes on the order of hours and, in extreme cases, days. Fortunately, computer time is significantly less expensive than engineering time. Second, the quality of the result depends upon the quality of the detailed analysis. In this regard, design experience is still valuable, though not as critical as in the manual design approach.

In order to utilize the optimization‐based design process, it is clearly necessary to be able to optimize mathematical functions. For design purposes, we will be optimizing the objective function, which we will also refer to as a fitness function. Optimization is a broad subject, which has been the subject of a strong and sustained interest of a host of researchers over the years. The purpose of this chapter is to introduce the subject to an extent sufficient to enable the reader to utilize an optimization‐based design process for power magnetic devices. More thorough study of optimization methods will serve every engineer well; for a good textbook devoted to the subject the reader is referred to Chong and Żak [1].

Before discussing optimization algorithms, it is appropriate to discuss some properties of objective functions that are relevant to their optimization, as these properties determine the effectiveness of one optimization approach relative to another.

As we proceed to do this, note that throughout this work, scalar variables are normally in italic font (for example, x ) while vector and matrices are bold nonitalic (for example, x). Functions of all dimensionalities are denoted by nonitalic nonbold font (for example, x( θ )). Brackets in equations are associated with iteration number in iterative methods.

In considering the properties of the objective function, it is appropriate to begin by defining our parameter vector, which will be denoted as x. The domain of xis referred to as the search space and will be denoted Ω, which is to say we require x∈ Ω. The elements of parameter vector xwill include those variables of a design that we are free to select. In general, some elements of xwill be discrete in nature while others will be continuous. An example of a discrete element might be one that designates a material type from a list of available materials. A geometrical parameter such as the length of a motor would be an example of an element that can be selected from a continuous range. If all members of the parameter vector are discrete, the search space is described as being discrete. If all members of the search space are continuous (in the set of real numbers), the search space is said to be continuous. If the elements of xinclude both discrete and continuous elements, the search space is said to be mixed. It is assumed that the function that we wish to optimize is denoted f( x). We will assume that f( x) returns a vector of dimension m of real numbers, that is, f( x) ∈ ℝ m, where m is the number of objectives we are considering. For most of this chapter, we will merely consider f( x) to be a mathematical function for which we wish to identify the optimizer of; however, in Section 1.9, and in the rest of this book for that matter, we will focus on how to construct f( x) so as to serve as an instrument of engineering design.

For this section, let us focus on the case where all elements of xare real numbers so that x∈ ℝ n, where ℝ ndenotes the set of real numbers of dimension n and where the number of objectives is one (that is, m = 1) so that f( x) is a scalar function of a vector argument. Finally, let us suppose we wish to minimize f( x). A point x *is said to be the global minimizer of f over Ω provided that

(1.2-1)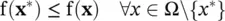

where ∀ is read as “for all” and Ω\{ x *} denotes the set Ω less the point x *. If the ≤ is replaced by <, then x *is referred to as the strict global minimizer.

As stated previously, the function f( x) can have properties that make it easier or more difficult to find the global minimizer. Some of these properties are depicted in Figure 1.3. An example of a feature that makes it more difficult to find the global minimizer is a discontinuity as shown in Figure 1.3(a). Therein Ω = [ x mn, x mx] and the discontinuity is at x = x a. In this case, the discontinuity results in a point where the function’s derivative is undefined. Since many optimization algorithms use the derivative of the function as part of the algorithm, such behavior can be problematic. In general, any problem with a discrete or mixed search space will have a discontinuous objective.