Scott D. Sudhoff - Power Magnetic Devices

Many classical optimization methods are very effective if they initialized to be close to the solution. This is because many functions are “locally” convex. At the same time, while GAs are often very effective at getting close to a global optimum, they may not always converge rapidly from a good approximation of a solution to the exact solution. This suggests a combination of the two approaches, wherein the best individual of the final population is used to initialize a classical optimization method. To this end, the Nelder–Mead simplex method [1] is particularly attractive because it does not require gradients or Hessians. In performing such an optimization, it is normally the case that in problems with a mixed search space, those genes that represent discrete choices are held fixed.

Before concluding this section, it is interesting to place all of the aforementioned operators into a single block diagram so that the relationships between the operators can be made clear. This is illustrated in Figure 1.14. Therein, initialization and the first fitness evaluation are as in the canonical GA diagramed in Figure 1.8. Next, the scaling algorithm is (optionally) employed. Note that the input and output of the scaling operator is the population P[ k ]; the same symbol for the input and output is used since the scaling operator does not operate on the population; it merely adjusts fitness values. The same is true of the diversity control operator, if utilized. Next, the selection operator creates a mating pool M[ k ]. Based on the mating pool, the mating, crossover, segregation, and mutation operators yield a population of children C[ k ].

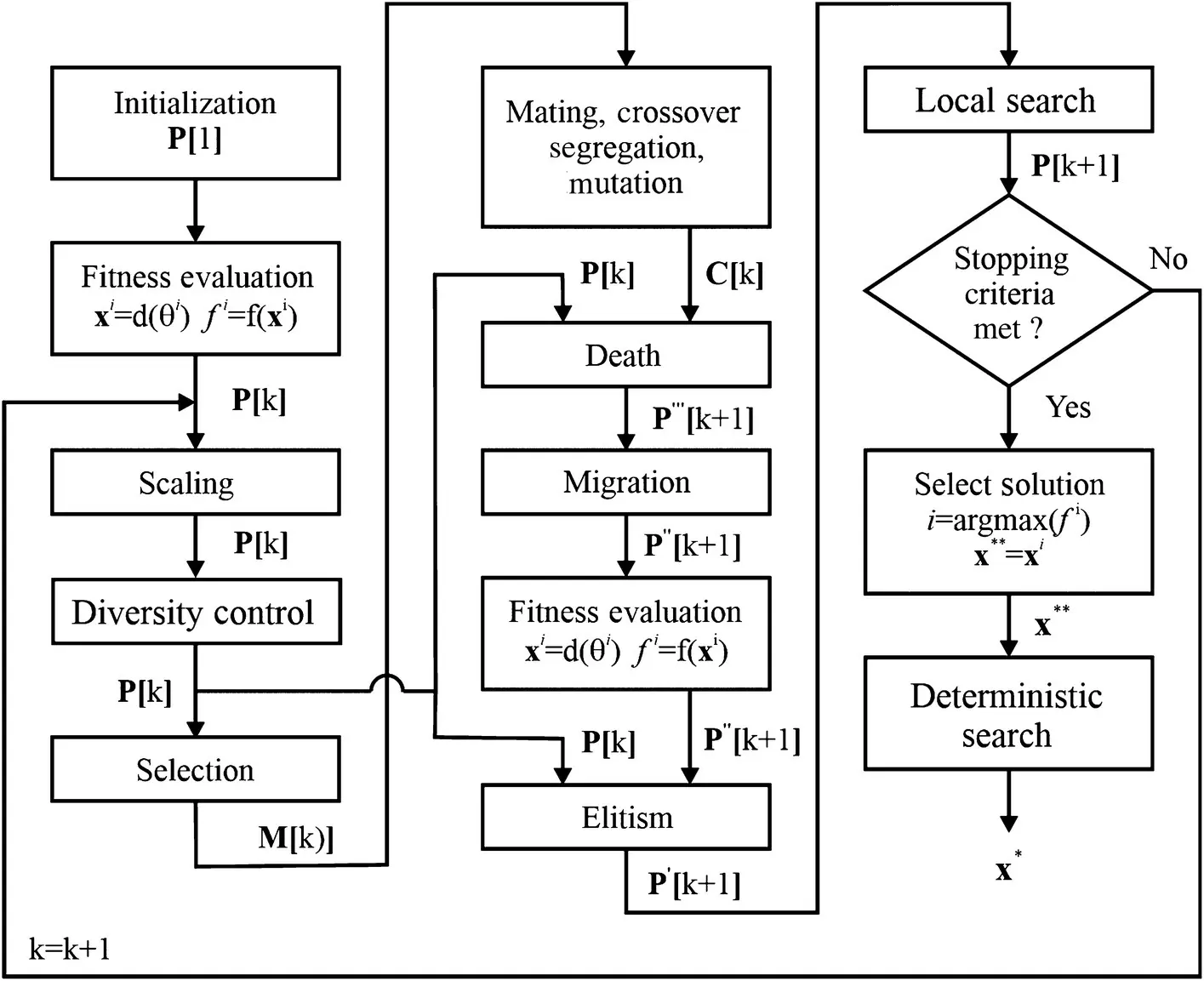
Figure 1.14 Enhanced real‐coded genetic algorithm.

The death algorithm selects a member of the current population to be replaced by the children, yielding the beginnings of the next generation, P ‴[ k + 1]. The primes are used because this population will be modified before becoming the next generation. First the migration operator will be applied, which may occasionally move individuals from one region to another. This yields P ″[ k + 1]. Next, the gene values are decoded and the fitness evaluated. The result is again denoted P ″[ k + 1] since the population itself does not change. The elitism operator is then applied, which compares the most fit individual of the previous population P[ k ] to the most fit individual in P ″[ k + 1] and replaces that individual if appropriate. This yields population P ′[ k + 1]. The local search operator is employed to generate P[ k + 1].

Once the next generation is formed, the stopping criterion is checked. Often, the stopping criterion is a check to see if a sufficient number of generations have passed. If the stopping criterion has not been met, the process repeats, starting with scaling. If the stopping criterion has been met, then an estimate of the solution x **is selected as the most fit individual of the population. This estimate can then be passed to a deterministic optimization algorithm for further refinement, yielding x *.

The algorithm depicted in Figure 1.14is probably more involved than is typical, because many optional operators have been used. For example, diversity control does not have to be used. Scaling is not necessary when using tournament or when the fitness values are always positive. A separate death algorithm is not necessary if the entire population is replaced by children. Random and deterministic search routines are often not used. Of the optional algorithms, elitism is fairly important. In addition, although not as commonly employed as elitism, the migration operator has been shown to have a significant impact on performance. Clearly, there is a wide variety of GA operators, and many books have been written on this subject. The reader is referred to references [4,5,8,9] for just a few of these. The good news is that almost all variations are effective optimization engines—they vary primarily in how quickly they converge and their probability of finding global solutions.

Much of our focus in this chapter has focused on the single‐objective optimization of an objective or fitness function f( x ). However, in the case of design problems, it is normally the case that there are multiple objectives of interest. In this section, we begin our consideration of the multi‐objective optimization problem.

Let us begin our discussion by the consideration of some designs of an electric motor. Suppose we are designing a motor and wish to minimize material cost and also to minimize loss. Further, suppose that we had eight designs available, each of which met all specifications for the machine, but each of which had a different cost and a different loss, as illustrated in Figure 1.15. Therein, each number listed is an index of a design. Thus, the x above point 1 has coordinates given by f( x 1).

Now let us consider the question of which design is the best. Let us first compare design 5 to design 7 (again using our shorthand notation of using a 5 to designate x 5). Design 7 has lower loss and lower cost than design 5, and so it is clearly better than design 5. Using similar reasoning, we can see that design 8 is better than designs {4,5,7}. Now let us compare design 8 to design 6. Design 8 has lower loss, but design 6 has lower cost. At this point, it is difficult to say which is better. This leads to the concept of dominance.

Consider two parameter vectors x aand x b. The parameter vector x ais said to dominate x bif f( x a) is no worse than f( x b) in all objectives and f( x a) is strictly better than f( x b) in at least one objective. The statement “ x adominates x b” is equivalent to the statement that “ x bis dominated by x a.” Returning to the example of the previous paragraph, we can say that design 8 dominates designs {4,5,7}.

Consider a set of parameter vectors denoted X. The nondominated set X nd⊂ Xis a set of parameter vectors that are not dominated by any other member parameter vector in X. In our example, X= {1, 2, …, 8} and X nd= {1, 6, 8}. The nondominated set can be viewed as the set of best designs.

If we consider the set of parameters to be the entire domain for the parameter vector (i.e., Ω) then the set of nondominated designs is referred to as the Pareto‐optimal set. The boundary defined by the objectives over this set is known as the Pareto‐optimal front. Pareto was an Italian engineer, economist, and philosopher who lived in the period of 1848–1923 (overlapping Mendel and Darwin) and who, besides his work in multi‐objective optimization, formulated the Pareto principle that 80% of effects stem from 20% of causes (and that 80% of wealth is owned by 20% of the population).

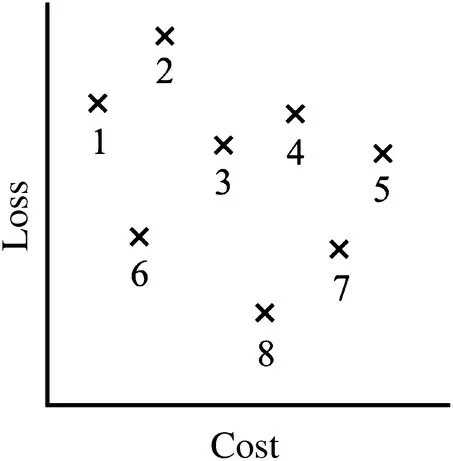
Figure 1.15 Motor performance objective space.