Oscar Gabriel Caballero Martínez - Gráficos por computadora usando JOGL

25. gl.glVertex2f(0.0f, yf);

26. gl.glEnd();

27. }

28. public void dibujaSeno(GL2 gl){

29. double inc, x;

30. inc=Math.PI/50;

31. glColor3d(15/256.0, 31/256.0, 172/256.0);

32. gl.glLineWidth(5f);

33. gl.glBegin(GL2.GL_LINE_STRIP);

34. for(x=-9;x<=9;x+=inc){

35. gl.glVertex2d(x, Math.sin(x));

36. }

37. gl.glEnd();

38. }

Código 3.2 GraficasTrigonometricas.java

De la línea 18 a la 27 se tiene la función dibujaEjes que dibuja los ejes de la gráfica con un grosor de línea de 10 pixeles (línea 19), de color negro (línea 20) y con dos vértices para el valor de x inicial y x final; a su vez, dos vértices para el eje y (líneas de la 22 a la 25). Posteriormente se transcribe la función dibujaSeno que dibuja la gráfica del seno (x) desde -9 hasta 9 y los puntos de los vértices se equidistan una longitud de π/50; como se podrá observar en el ciclo for de la línea 34. De la línea 33 a la línea 37, se observa que se genera una serie de vértices que son unidos por la característica GL_LINE_STRIP que, se puede ver en la figura 3.3, une todos los vértices con líneas desde el primero hasta el último. Como los vértices están muy juntos, a simple vista se observa una curva, pero todas son líneas rectas.

Se puede observar que en el método display , en la línea 14, se manda llamar al método dibujaEjes con los parámetros: el objeto gl, los valores de punto flotante -9f del x inicial, 9f del x final, -1f del y inicial y 1f del y final. En la línea 15 se invoca al método dibujaSeno que lleva como parámetro al objeto gl para poder dibujar la gráfica. Por ello se dibujan los ejes primero y encima de ellos a la gráfica del seno; esta manera de dibujar se analizará más adelante en el trabajo.

Práctica. Para cada función trigonométrica siguiente se debe poner un color diferente para dibujar la gráfica.

1. Coseno

2. Tangente

3. Cotangente

4. Secante

5. Cosecante

Continuando con el manejo de las gráficas primitivas, se realizará el fractal del triángulo de Sierpinsky. En una clase llamada Sierpinsky se modifcan los métodos siguientes, agregando además el método dibujaTriangulo .

1. public void init(GLAutoDrawable glad) {

2. GL2 gl = glad.getGL().getGL2();

3. GLU glu = new GLU();

4. gl.glClearColor(1,1,1,0);

5. gl.glMatrixMode(GL2.GL_PROJECTION);

6. glu.gluOrtho2D (0.0, 10.0, 0.0, 10.0);

7. gl.glMatrixMode(GL2.GL_MODELVIEW);

8. gl.glLoadIdentity();

9. }

10. public void display(GLAutoDrawable drawable)

11. {

12. GL2 gl = glad.getGL().getGL2();

13.

14. gl.glClear(GL2.GL_COLOR_BUFFER_BIT);

15. gl.glLoadIdentity();

16. gl.glPointSize(3.0f);

17. gl.glColor3d(24/255.0,128/255.0,21/255.0);

18. dibujaTriangulo(gl);

19. gl.glFlush();

20. }

21. public void reshape(GLAutoDrawable glad, int i, int i1, int i2, int i3) {

22. GL2 gl = glad.getGL().getGL2();

23. gl.glViewport(0, 0, i2, i3);

24. }

25. public void dibujaTriangulo(GL2 gl){

26. double ax,ay,bx,by,cx,cy,px,py;

27. double r;

28. int i,rprima;

29. i=0;

30. ax=1.0;

31. ay=1.0;

32. bx=5.0;

33. by=9.0;

34. cx=9.0;

35. cy=1.0;

36. px=9.0;

37. py=9.0;

38. gl.glBegin(GL2.GL_POINTS);

39. gl.glVertex2d(ax,ay);

40. gl.glVertex2d(bx,by);

41. gl.glVertex2d(cx,cy);

42. do{

43. gl.glVertex2d(px,py);

44. r=Math.random()*1000;

45. rprima = (int)r%3;

46. switch(rprima){

47. case 0: px=(px+ax)/2;

48. py=(py+ay)/2;

49. break;

50. case 1: px=(px+bx)/2;

51. py=(py+by)/2;

52. break;

53. case 2: px=(px+cx)/2;

54. py=(py+cy)/2;

55. break;

56. }

57. i++;

58. }while(i<10000);

59. gl.glEnd();

60. }

Código 3.3 Sierpinsky.java

La idea para construir el triángulo se basa en que se tienen tres puntos fijos A, B y C, definidos desde la línea 30 a la 35, dentro del método dibujaTriangulo , y un cuarto punto P que se define en las líneas 36 y 37. El algoritmo trabaja tomando cualquier punto A, B y C al azar; ya que se tiene, se calcula el punto medio entre el punto escogido y el punto P y el resultado se asigna al punto P; esto se hace desde la línea 44, donde r toma el valor aleatorio ( Math.random()*1000 ), la línea 45 donde rprima toma el módulo 3 del valor truncado de r ( (int)r%3 ) que puede tomar los valores de 0, 1 y 2; de la línea 46 a la línea 56, dependiendo del valor de rprima se calcula el punto medio requerido. Esto se aplica hasta que el valor de i alcance el valor de 10000 (de la línea 42 a la 58). Al finalizar genera la figura 3.7.

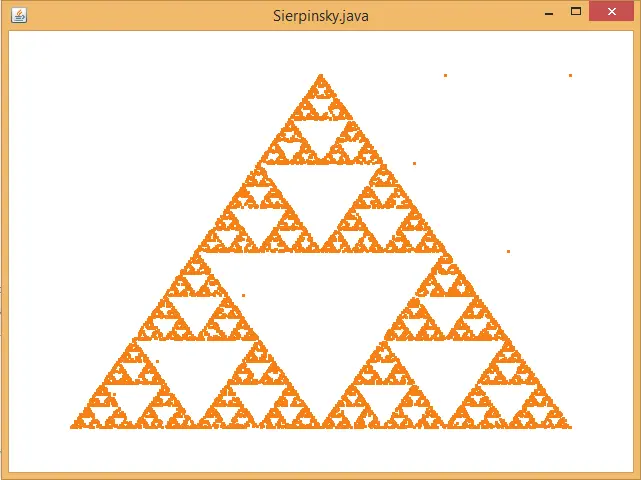
Figura 3.7 Salida del triángulo de Sierpinsky

Fuente: Elaboración propia.

Para continuar con las metodologías de programación llevadas al momento se construirá otra versión de la clase anterior que se llamará SierpinskyV2 , que consiste en apoyarse de una clase, la cual llevará el nombre de MisPuntos2D .

1. import com.jogamp.opengl.GL2;

2. public class MisPuntos2D {

3. double x,y;

4. MisPuntos2D(){

5. x = y = 0.0;

6. }

7. MisPuntos2D(double px, double py){

8. x = px;

9. y = py;

10. }

11. void puntoMedio(MisPuntos2D p){

12. x = (x+p.x)/2;

13. y = (y+p.y)/2;

14. }

15. void dibuja(GL2 gl){

16. gl.glBegin(GL2.GL_POINTS);

17. gl.glVertex2d(x, y);

18. gl.glEnd();

19. }

20. }

Código 3.4 MisPuntos2D.java

Las características de esta clase son los valores de las coordenadas x e y línea 3. En la línea 1 se importa el paquete que contiene a la clase GL2, que nos ayudará a dibujar el punto en dos dimensiones (ver líneas de la 15 a la 19). De las líneas 11 a la 14, el método puntoMedio recibe como parámetro un objeto MisPuntos2D y calcula el punto medio entre el parámetro y el objeto que manda llamar al método. Los constructores (líneas de la 4 a la 6 y de la 7 a la línea 10) funcionan de la siguiente forma: si no hay parámetros al momento de construir al objeto, el valor del punto es el origen, en cambio, si llegan dos valores como parámetros el punto es (px, py).

Para programar la nueva versión se genera una nueva clase llamada SierpinskyV2 y se sustituyen los métodos

• init

• display

• reshape

de la clase Sierpinsky a la clase SierpinskyV2 . Y en la línea 18 del método display se cambia por dibujaTrianguloV2(gl).

Y se transcribe el siguiente código

1. void dibujaTrianguloV2(GL2 gl){

2. MisPuntos2D A,B,C,P;

3. double r;

4. int i=0,rprima;

5. A = new MisPuntos2D(1,1);

6. B = new MisPuntos2D(5,9);

7. C = new MisPuntos2D(9,1);

8. P = new MisPuntos2D(4,4);

9. A.dibuja(gl);

10. B.dibuja(gl);

11. C.dibuja(gl);

12. do{

13. P.dibuja(gl);

14. r = Math.random()*10000;

15. rprima = (int)r%3;

16. switch(rprima){

17. case 0: P.puntoMedio(A);

18. break;

19. case 1: P.puntoMedio(B);

20. break;

21. case 2: P.puntoMedio(C);

22. break;

23. }

24. i++;

25. }while(i<10000);

26. }

Código 3.5 SierpinskyV2.java

Este código genera la salida como se presenta en la figura 3.7, salvo el punto P , que se encuentra en otro lugar. La ventaja de este código, a diferencia del anterior, es que contiene menos línea y es un poco más fácil de entender qué está haciendo, ya que al utilizar la clase MisPuntos2D ayuda a su comprensión. Por ejemplo, el cálculo del punto medio entre P y algún otro punto (ver líneas 17, 19 y 21). Además de que la clase MisPuntos2D puede ser utilizada por otro programa que maneje las mismas características.