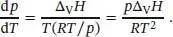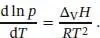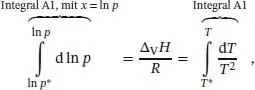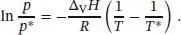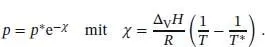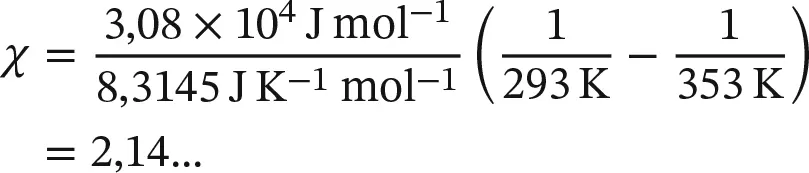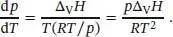
und daraus durch Umstellen die Clausius‐Clapeyron‐Gleichungfür die Abhängigkeit des Dampfdrucks von der Temperatur:
(4.11) 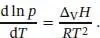
(Dazu haben wir d x / x = d ln x verwendet.) Wie auch die Clapeyron‐Gleichung (die exakt gilt) ist die Clausius‐Clapeyron‐Gleichung (die nur eine Näherung ist) entscheidend für das Verständnis der Gestalt von Phasendiagrammen, insbesondere der Lage und Form der Phasengrenzen flüssig/gasförmig und fest/gasförmig. Mit ihrer Hilfe können wir voraussagen, wie sich der Dampfdruck mit der Temperatur und die Siedetemperatur mit dem Druck ändert. Wenn wir noch voraussetzen, dass die Verdampfungsenthalpie nicht von der Temperatur abhängt, können wir Gl. (4.11)integrieren,
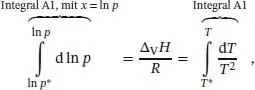
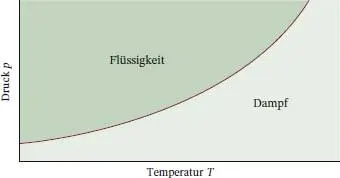
Abb. 4.19 Eine typische Phasengrenzlinie flüssig/gasförmig; sie entspricht einer Auftragung des Dampfdrucks als Funktion der Temperatur. Die Phasengrenzlinie endet am kritischen Punkt (hier nicht eingezeichnet).
und wir erhalten
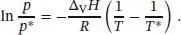
wobei p * der Dampfdruck bei der Temperatur T * ist; p gehört entsprechend zu T . Da das Integral auf der linken Seite ln( p / p *) liefert, lautet die Beziehung zwischen den beiden Dampfdrücken folglich
(4.12) 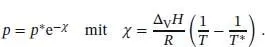
Diese Funktion beschreibt den Verlauf der Phasengrenzlinie flüssig/gasförmig (Dampfdruckkurve) in Abb. 4.19. Sie endet bei der kritischen Temperatur T krit, da oberhalb dieser keine flüssige Phase mehr existiert.
Mithilfe der Clausius‐Clapeyron‐Gleichung ( Gl. (4.12)) können wir den Dampfdruck einer Flüssigkeit ausgehend von ihrem Normalsiedepunkt (der Temperatur, bei der der Dampfdruck 1,00 atm (101 kPa) ist) bei beliebiger Temperatur näherungsweise berechnen. Der Normalsiedepunkt von Benzol ist beispielsweise 80 °C (353 K); aus Tab. 3.2in Abschn. 3.2entnehmen wir die Standardverdampfungsenthalpie von Benzol, Δ V H ⊖= 30,8 kJ mol −1. Daraus berechnen wir den Dampfdruck von Benzol bei 20 °C (293 K):
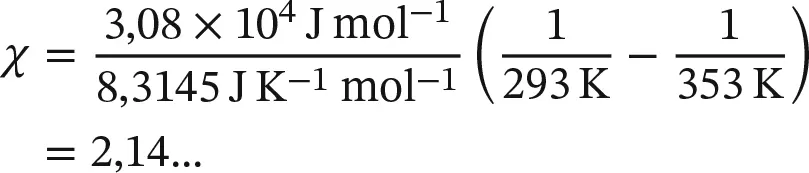
Diesen Wert und p * = 101 kPa setzen wir in Gl. (4.12)ein; das Ergebnis ist 12 kPa. Der experimentell bestimmte Wert liegt bei 10 kPa.
HinweisWegen der Empfindlichkeit von Exponentialfunktionen gegenüber Veränderungen des Exponenten sollte man bei numerischen Rechnungen wie dieser vermeiden, Zwischenergebnisse auszurechnen und mit gerundeten Werten fortzufahren.
(d) Die Phasengrenzlinie fest/gasförmig
In allen für die Phasengrenze flüssig/gasförmig abgeleiteten Beziehungen tauschen wir einfach die Verdampfungsenthalpie gegen die Sublimationsenthalpie Δ Sub H aus. Da die Sublimationsenthalpie größer ist als die Verdampfungsenthalpie (Δ Sub H = Δ Sm H + Δ V H ), kann man der Gleichung entnehmen, dass in der Nähe des Schnittpunkts beider Kurven (im Tripelpunkt, siehe Abb. 4.20) die Sublimationsdruckkurve steiler ansteigt als die Dampfdruckkurve.
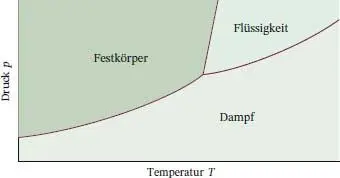
Abb. 4.20 Die Steigung der Phasengrenzlinie fest/gasförmig ist in der Nähe des Schnittpunkts (Tripelpunkts) steiler als die der Phasengrenzlinie flüssig/gasförmig, weil die Sublimationsenthalpie größer ist als die Verdampfungsenthalpie, aber die Temperaturen, die in der Clausius‐Clapeyron‐Gleichung für die Steigung auftreten, ungefähr gleich groß sind.
Die Schmelzenthalpie von Eis am Tripelpunkt von Wasser (6,1 mbar, 273 K) weicht nur geringfügig vom Wert der Standardschmelzenthalpie am Gefrierpunkt ab; dieser beträgt 6,008 kJ mol −1. Die Verdampfungsenthalpie bei derselben Temperatur ist 45,0 kJ mol −1(die Abweichung vom Wert bei einem Druck von 1 bar ist gering). Die Sublimationsenthalpie ist somit 51,0 kJ mol −1. Die Beziehungen für die Steigungen der Phasengrenzlinien (a) flüssig/gasförmig bzw. (b) fest/gasförmig am Tripelpunkt sind, gemäß Gl. (4.11),
1 (a)
2 (b)
Bei einer Auftragung von ln p gegen T finden wir, dass die Steigung der Phasengrenzlinie fest/gasförmig in der Nähe des Schnittpunkts (Tripelpunkts) steiler ist als die der Phasengrenzlinie flüssig/gasförmig.
1 1. Das chemische Potenzial einer Substanz nimmt bei steigender Temperatur proportional zu ihrer molaren Entropie ab.
2 2. Das chemische Potenzial einer Substanz nimmt bei steigendem Druck proportional zu ihrem Molvolumen zu.
3 3. Wenn auf eine kondensierte Phase Druck ausgeübt wird, steigt ihr Dampfdruck.
4 4. Die Clapeyron‐Gleichung gibt einen Ausdruck für die Steigung einer Phasengrenzlinie an.
5 5. Die Clausius‐Clapeyron‐Gleichung ist eine Näherung, die die Steigung der Phasengrenzlinie flüssig/gasförmig als Funktion der Verdampfungsenthalpie ausdrückt.
Die wichtigsten Gleichungen auf einen Blick
| Stichwort |
Gleichung |
Anmerkung |
Nummer |
| Variation von μ mit der Temperatur |
( ∂ μ / ∂ T ) p= − S m |
μ = G m |
Gl. (4.3a) |
| Variation von μ mit dem Druck |
( ∂ μ / ∂ p ) T= V m |
|
Gl. (4.3b) |
| Dampfdruck beim Ausüben eines Drucks |
p = p *e Vm (l) ΔP/RT |
Δ P = P − p * |
Gl. (4.4) |
| Clapeyron‐Gleichung |
d p /d T = Δ Trans S /Δ Trans V |
|
Gl. (4.6a) |
| Clausius‐Clapeyron‐Gleichung |
d ln p /d T = Δ V H / R T2 |
gilt unter der Annahme, dass V m(g) ≫ V m(l) oder V m(s) ist, und der Dampf sich wie ein ideales Gas verhält |
Gl. (4.11) |
Übungsteil Fokus 4 – Physikalische Umwandlungen reiner Stoffe
Behandeln Sie alle Gase als ideal, sofern nicht ausdrücklich etwas anderes verlangt ist. Thermochemische Daten sind für 298,15 K angegeben, sofern nicht ausdrücklich etwas anderes erwähnt ist.
Читать дальше