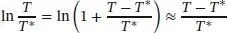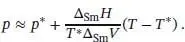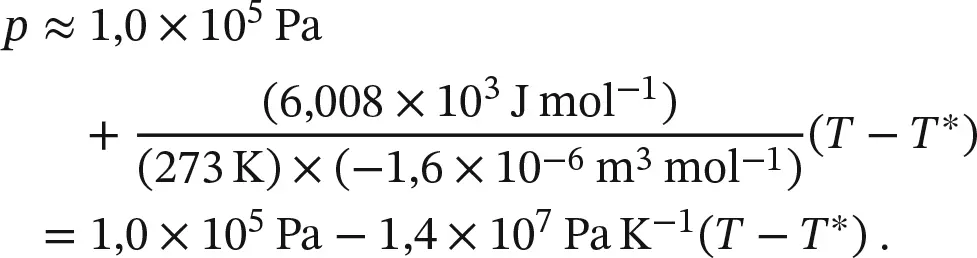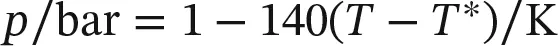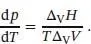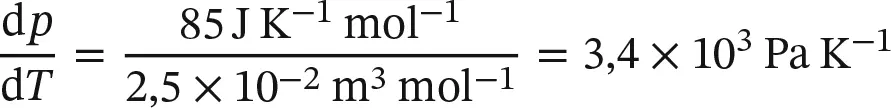(b) Die Phasengrenzlinie fest/flüssig
Der Schmelzvorgang findet bei einer Temperatur T statt und verläuft unter Änderung der molaren Enthalpie des Systems um Δ Sm H . Daraus ergibt sich die molare Schmelzentropie zu Δ Sm H / T (siehe Abschn. 3.2); alle Punkte auf der Phasengrenzlinie entsprechen einem Gleichgewicht zwischen den Phasen, daher entspricht T auch der Übergangstemperatur T Trans. Die Clapeyron‐Gleichung für diesen Vorgang lautet
(4.7) 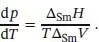
Δ Sm V ist die Änderung des molaren Volumens beim Schmelzen. Die Schmelzenthalpie ist immer positiv (die einzige Ausnahme ist Helium‐3), die Volumenänderung ist normalerweise ebenfalls positiv und stets relativ klein. Folglich ist die Steigung d p /d T groß und im Allgemeinen positiv ( Abb. 4.17).
Eine mathematische Beschreibung der Phasengrenzlinie erhalten wir durch Integration von d p /d T unter der Annahme, dass Δ Sm H und Δ Sm V so wenig von der Temperatur abhängen, dass sie als Konstanten behandelt werden können. Wenn die Schmelztemperatur bei dem Druck p * gleich T * und bei dem Druck p gleich T ist, haben wir folgende Integration auszuführen:
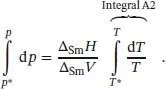
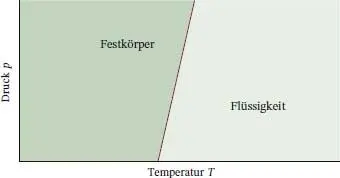
Abb. 4.17 Eine typische Phasengrenzlinie fest/flüssig steigt steil an. Daraus lässt sich schließen, dass die Schmelztemperatur steigt, wenn der Druck zunimmt. Die meisten Stoffe verhalten sich so, Wasser ist eine wichtige Ausnahme.
Wir erhalten als Näherungsgleichung für die Phasengrenzlinie fest/flüssig
(4.8) 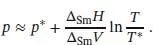
Diese Gleichung wurde von einem Mitglied der Familie Thomson erstmals formuliert – von James, dem Bruder des späteren Lord Kelvin.
Wenn T nahe bei T * liegt, kann man den Logarithmus in guter Näherung mithilfe der Reihenentwicklung 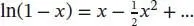 (siehe „Toolkit 12: Reihenentwicklungen“ in Abschn. 5.2) als
(siehe „Toolkit 12: Reihenentwicklungen“ in Abschn. 5.2) als
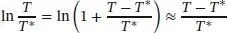
schreiben, wobei alle Terme außer dem ersten vernachlässigt wurden; damit wird
(4.9) 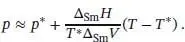
Dies ist eine Geradengleichung für p als Funktion von T (siehe Abb. 4.17).
Die Schmelzenthalpie von Eis bei 0 °C (273 K) und 1 bar ist 6,008 kJ mol −1, und das Schmelzvolumen ist −1,6 cm 3mol −1. Gemäß Gl. (4.9)ist die Phasengrenzlinie fest/flüssig von Wasser näherungsweise gegeben durch
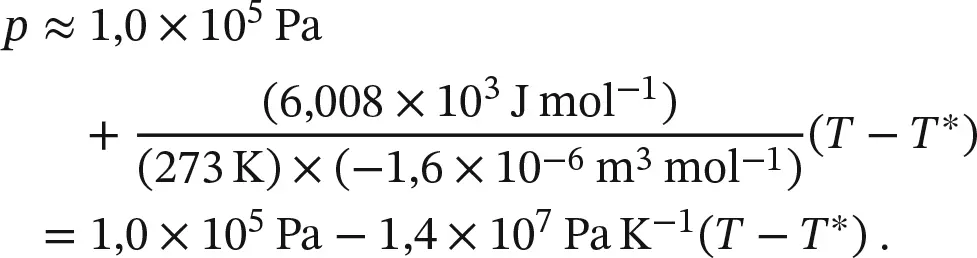
Als Geradengleichung für die grafische Auftragung, die in Abb. 4.18gezeigt ist, verwenden wir also
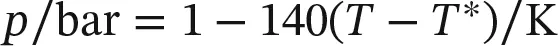
mit T * = 273 K.
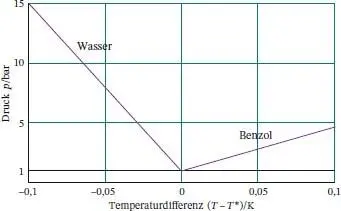
Abb. 4.18 Die Phasengrenzlinie fest/flüssig (die Schmelzkurve) für Wasser, wie sie in Illustration 4.12berechnet wird. Zum Vergleich ist die entsprechende Phasengrenzlinie von Benzol gezeigt.
(c) Die Phasengrenzlinie flüssig/gasförmig
Die Verdampfungsentropie eines Stoffs bei der Temperatur T ist gleich Δ V H / T ; alle Punkte auf der Phasengrenzlinie entsprechen einem Gleichgewicht zwischen den Phasen, daher entspricht T auch der Übergangstemperatur T Trans. Die Clapeyron‐Gleichung der Phasengrenzlinie flüssig/gasförmig lautet demzufolge
(4.10) 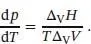
Die Verdampfungsenthalpie ist stets positiv, und Δ V V ist ein großer, ebenfalls positiver Wert. Die Ableitung d p /d T ist daher auch positiv, aber wesentlich kleiner als für die Phasengrenze fest/flüssig. Der Differenzialquotient d T /d p ist folglich groß, weshalb die Siedetemperatur wesentlich empfindlicher auf Druckänderungen reagiert als die Schmelztemperatur.
Beispiel 4.2: Der Einfluss des Drucks auf den Siedepunkt
Bestimmen Sie, wie groß der Einfluss einer Erhöhung des Drucks auf den Siedepunkt einer Flüssigkeit in typischen Fällen ist.
VorgehensweiseUm Gl. (4.10)verwenden zu können, müssen wir die rechte Seite abschätzen. Am Siedepunkt entspricht der Term Δ V H / T gerade der Trouton‐Konstante ( Abschn. 3.2). Das Molvolumen von Gasen ist viel größer als das von Flüssigkeiten, wir schreiben daher Δ V V = V m(g)− V m(l)≈ V m(g) und setzen für V m(g) das Molvolumen eines idealen Gases ein (dies ist zumindest für kleine Drücke eine akzeptable Näherung).
LösungEntsprechend der Regel von Pictet‐Trouton ist Δ V H / T ≈ 85 J K −1mol −1; das Molvolumen eines idealen Gases beträgt bei Atmosphärendruck und einer Temperatur etwas oberhalb der Zimmertemperatur etwa 25 dm 3mol −1. Durch Einsetzen der Zahlenwerte erhalten wir
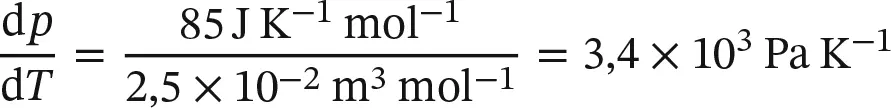
(mit 1 J = 1 Pa m 3) oder umgerechnet 0,034 atm K −1; damit ist d T /d p = 29 K atm −1. Eine Druckerhöhung um 0,1 atm (0,01 MPa, 0,1 bar) hat eine Verschiebung der Siedetemperatur um +3K zur Folge.
Selbsttest 4.2
Wiederholen Sie die Rechnung für die feste und die flüssige Phase von Kohlendioxid (Molmasse 44,0 g mol −1), die sich miteinander im Gleichgewicht befinden. Gegeben sind die Dichten mit 2,35 g cm −3bzw. 2,50 g cm −3.
[Antwort: 28 K atm −1]
Das Molvolumen eines Gases ist viel größer als das einer Flüssigkeit, sodass wir in guter Näherung Δ V V ≈ V m(g) setzen können, wie wir es in Beispiel 4.2bereits getan haben. Wenn ein ideales Gas vorliegt, gilt außerdem V m(g) = R T / p . Setzt man diese beiden Näherungen in die exakt gültige Clapeyron‐Gleichung ein, erhält man
Читать дальше

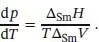
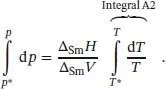

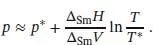
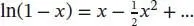 (siehe „Toolkit 12: Reihenentwicklungen“ in Abschn. 5.2) als
(siehe „Toolkit 12: Reihenentwicklungen“ in Abschn. 5.2) als