Peter W. Atkins - Physikalische Chemie

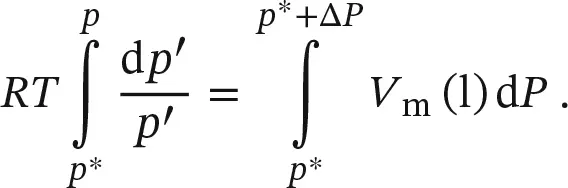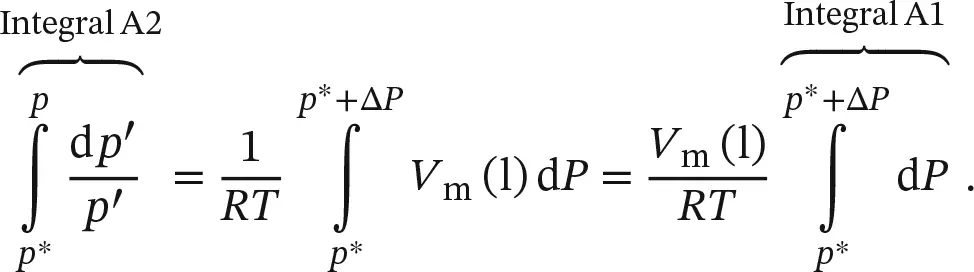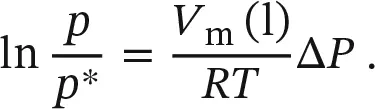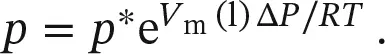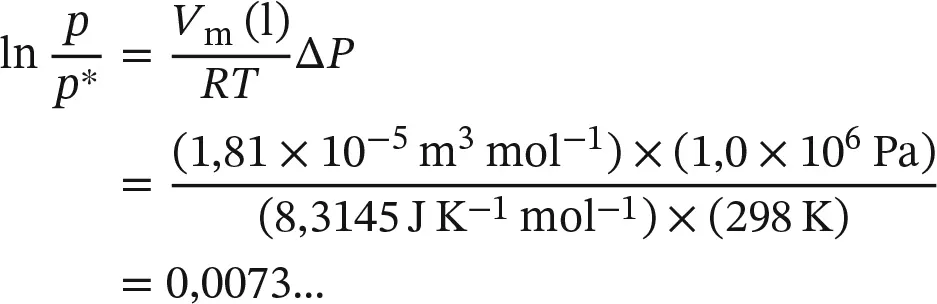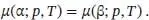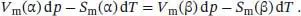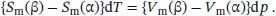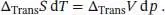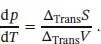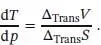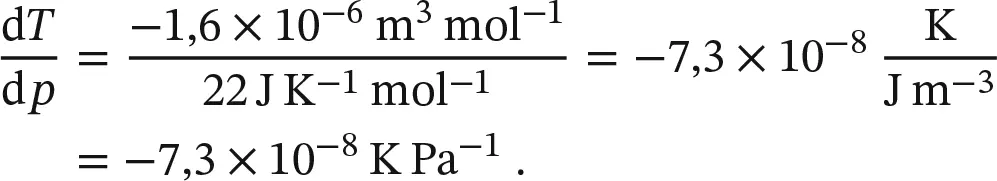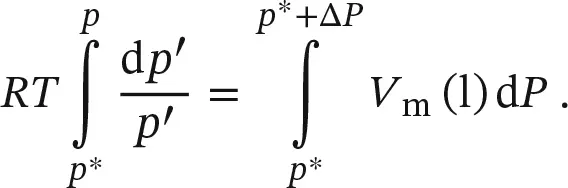
(Im ersten Integral haben wir die Schreibweise der Variablen im Integrand von p nach p′geändert, um eine Verwechslung mit der oberen Integrationsgrenze p auszuschließen.)

Schritt 4 Integration der Beziehung .

Wir teilen beide Seiten durch RT und nehmen an, dass das molare Volumen der Flüssigkeit im kleinen betrachteten Druckbereich konstant ist:

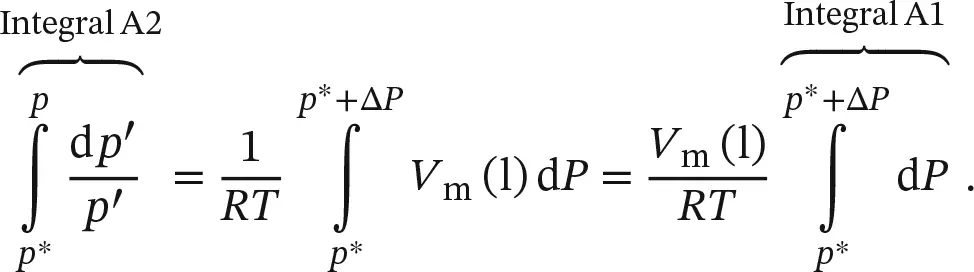
Die Integration ist nun nicht schwierig und führt zu

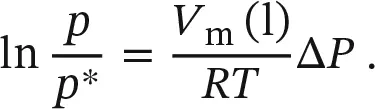
Wegen e lnx= x können wir dies umstellen zu

(4.4)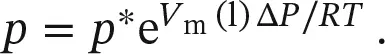

Gleichung (4.4)ist die quantitative Beziehung zwischen dem Dampfdruck p unter einem ausgeübten Druck Δ P und dem Dampfdruck p * ohne zusätzlichen äußeren Druck.

Wenn die kondensierte Phase, auf die Druck ausgeübt wird, eine Flüssigkeit ist, muss man mit einer Komplikation rechnen, die wir hier nicht weiter diskutieren wollen: Das Inertgas kann sich in der Flüssigkeit lösen und so deren Eigenschaften verändern. Weitere Probleme entstehen durch zwischenmolekulare Anziehungskräfte der Spezies in der Gasphase, wodurch der Flüssigkeit Moleküle entzogen werden können (diesen Effekt nennt man Gassolvatation).

Wasser hat bei 25 °C eine Dichte von 0,997 g cm −3und folglich ein molares Volumen von 18,1 cm 3mol −1. Wenn der Druck um 10 bar zunimmt (also Δ P = 1,0 × 10 6Pa), so ist

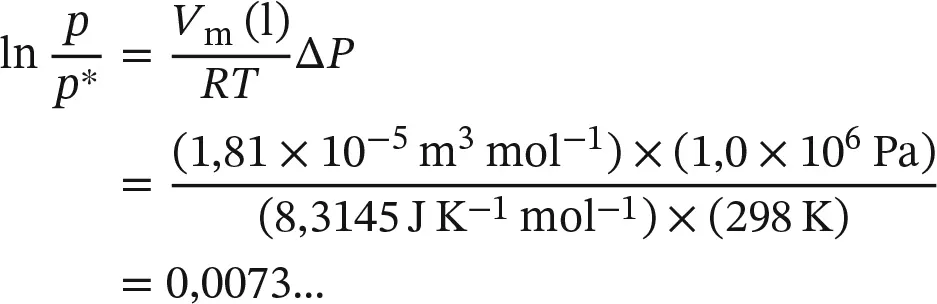
(mit 1 J = 1 Pa m 3). Es ergibt sich p = 1,0073 p *, also eine Zunahme um 0,73 Prozent.

Die genaue Lage der Phasengrenzlinien – der Wertepaare von Druck und Temperatur, bei denen zwei Phasen koexistieren – finden wir, indem wir die Tatsache ausnutzen, dass zwei Phasen, die sich miteinander im Gleichgewicht befinden, gleiche chemische Potenziale besitzen. Für zwei Phasen α und β bedeutet das

(4.5)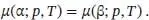

Die Lösung dieser Beziehung ist die Gleichung der Phasengrenzlinie in Form einer Funktion p = p ( T ).

Das charakteristische Merkmal der Phasengrenzlinien, das sich am einfachsten beschreiben lässt, ist ihre Steigung; wir beginnen daher, indem wir eine Beziehung für d P /d T suchen. T und p sollen sich in infinitesimalen Schritten so ändern, dass das Gleichgewicht zwischen α und β stets erhalten bleibt. Zu Beginn sind die chemischen Potenziale beider Phasen gleich (da das Gleichgewicht eingestellt ist). Wenn man sich auf die beschriebene Weise zu einem anderen Punkt der Phasengrenzlinie bewegt ( Abb. 4.16), ist diese Bedingung immer erfüllt (da das Gleichgewicht eingestellt bleibt). Daher kann man die Änderungen des chemischen Potenzials beider Phasen gleichsetzen, d μ (α) = d μ (β).

Gleichung (3.43) (d G = V d p − S d T ) gibt die Variation von G mit p und T an, und mit μ = G mfolgt, dass für jede der beiden Phasen d μ = − S md T + V md p ist. Also können wir anstelle der Beziehung d μ (α) = d μ (β) auch schreiben:

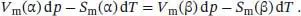
Hier sind S m(α) und S m(β) die molaren Entropien und V m(α) und V m(β) die molaren Volumina der jeweiligen Phase. Durch Zusammenfassen und Umformen dieser Gleichung erhalten wir

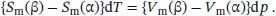
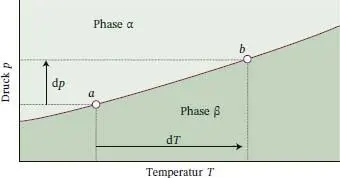
Abb. 4.16 Wenn Druck auf ein System ausgeübt wird, in dem sich zwei Phasen im Gleichgewicht befinden (am Punkt a ), so wird das Gleichgewicht gestört. Es kann durch eine Temperaturänderung wieder hergestellt werden; dabei geht das System in den Zustand b über. Daraus folgt, dass zwischen d p und d T ein Zusammenhang besteht, der dafür sorgt, dass das System bei Änderung einer der beiden Variablen im Gleichgewicht bleibt.

Die Änderung der (molaren) Entropie bei einem Phasenübergang, Δ Trans S , ergibt sich aus der Differenz der molaren Entropien der beiden Phasen, Δ Trans S = S m(β)− S m(α); entsprechendes gilt für die Änderungen der (molaren) Volumina, Δ Trans V = V m(β) − V m(α). Also gilt

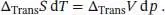
Daraus ergibt sich unmittelbar die Clapeyron‐Gleichung

(4.6a)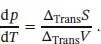

Die Clapeyron‐Gleichung ist ein exakter Ausdruck für die Steigung der Tangente an jeden beliebigen Punkt der Phasengrenzlinie; sie kann auf jedes Phasengleichgewicht eines beliebigen reinen Stoffs angewendet werden. Mit ihrer Hilfe können wir thermodynamische Daten für die Voraussage von Phasendiagrammen verwenden und deren Gestalt verstehen. Eine praktische Anwendung ist die Vorhersage des Verhaltens der Schmelz‐ und Siedepunkte bei einer Druckerhöhung; in diesem Zusammenhang wird die Clapeyron‐Gleichung meist in einer Form verwendet, bei dem Zähler und Nenner der Brüche auf beiden Seiten der Gleichung invertiert sind:

(4.6b)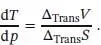

Das Standardvolumen des Übergangs von Eis zu flüssigem Wasser bei 0 °C ist −1,6 cm 3mol −1, und die entsprechende Standardentropie des Übergangs beträgt +22 J K −1mol −1. Die Steigung der Phasengrenzlinie fest/flüssig bei dieser Temperatur ist daher

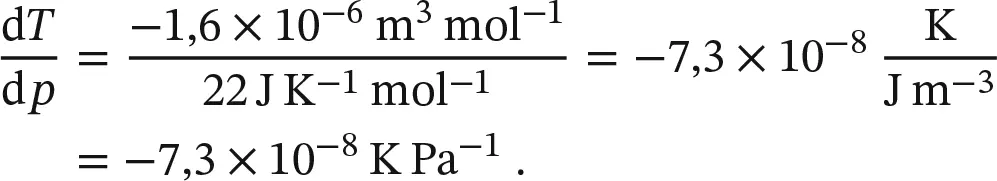
Dies entspricht −7,3 mK bar −1. Eine Druckerhöhung um 100 bar führt daher bei Wasser zu einer Gefrierpunktserniedrigung um 0,73 K.