Peter W. Atkins - Physikalische Chemie

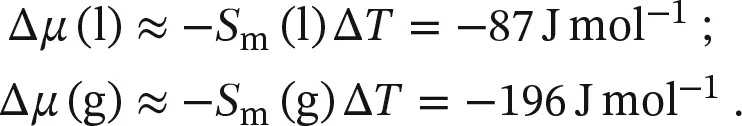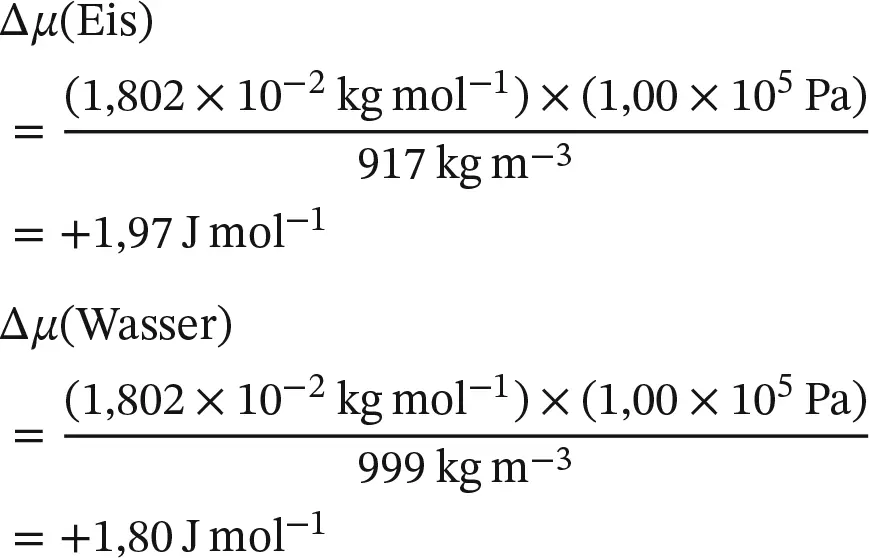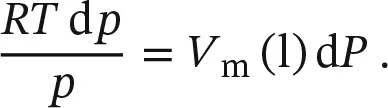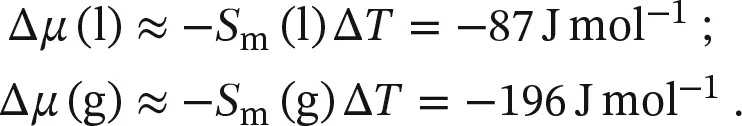
Bei 100 °C besitzen die beiden Phasen identische chemische Potenziale und liegen somit im Gleichgewicht vor. Bei 101 °C sind die chemischen Potenziale des Dampfes und der Flüssigkeit geringer als bei 100 °C; das chemische Potenzial des Dampfes hat sich allerdings um einen größeren Betrag reduziert. Daraus folgt, dass der Dampf bei der höheren Temperatur die stabile Phase ist, und die Flüssigkeit verdampft freiwillig.

Aus Gleichung (4.3b)können wir ablesen, dass das chemische Potenzial jeder reinen Substanz mit steigendem Druck zunimmt, weil V m> 0 ist. In den meisten Fällen gilt außerdem V m(l) > V m(s), sodass nach Gl. (4.3b)das chemische Potenzial der flüssigen Phase bei steigendem Druck stärker zunimmt als das der festen Phase. Die Folge ist, wie wir in Abb. 4.14a sehen, dass die Schmelztemperatur etwas ansteigt. Für Wasser gilt dagegen V m(l) < V m(s); ein Druckanstieg bewirkt hier für die feste Phase eine stärkere Zunahme des chemischen Potenzials als für die flüssige Phase. Dadurch sinkt die Schmelztemperatur ein wenig ( Abb. 4.14b).

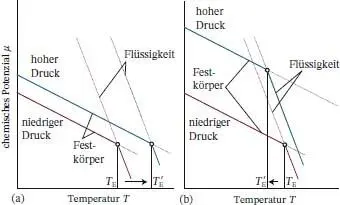
Abb. 4.14 Die Druckabhängigkeit des chemischen Potenzials eines Stoffs ist durch das molare Volumen der jeweiligen Phase gegeben. Die Druckabhängigkeit der chemischen Potenziale von fester und flüssiger Phase ist schematisch durch Geraden angedeutet (in Wirklichkeit sind die Linien gekrümmt); darunter sehen Sie die entsprechende Darstellung für die Schmelztemperatur. (a) In dem hier gezeigten Fall ist das Molvolumen der festen Phase kleiner als das der flüssigen Phase; daher steigt μ (s) weniger stark an als μ (l); die Schmelztemperatur nimmt zu. (b) In diesem Fall ist das Molvolumen des Feststoffs größer als das der Flüssigkeit (wie bei Wasser), μ (s) steigt stärker an als μ (l); die Schmelztemperatur wird erniedrigt.

Berechnen Sie, wie sich das chemische Potenzial von Wasser und Eis (jeweils bei 0 °C) ändert, wenn der Druck von 1 bar auf 2 bar ansteigt. Gegeben sind die Dichten von flüssigem Wasser (0,999 g cm −3) und Eis (0,917 g cm −3) unter diesen Bedingungen.

VorgehensweiseAus Gl. (4.3b)ist die Druckabhängigkeit des chemischen Potenzials eines nahezu inkompressiblen Stoffs bekannt: Δ μ = V mΔ p . Zur Lösung der Aufgabe müssen wir daher zunächst die Molvolumina beider Phasen kennen; wir erhalten sie aus der Dichte ρ und der Molmasse M gemäß V m= M / ρ . Die gesuchte Beziehung lautet dann Δ μ = M Δ p / ρ . Achten Sie auf die verwendeten Einheiten: Sie müssen die Dichte in Kilogramm pro Kubikmeter (kg m −3) und die Molmasse in Kilogramm pro Mol (kg mol −1) angeben; außerdem gilt 1 Pa m 3= 1 J.

LösungDie molare Masse von Wasser beträgt 18,02 g mol −1(1,802 × 10 −2kg mol −1); durch Einsetzen aller Zahlenwerte erhalten wir somit für eine Erhöhung des Drucks um 1,00 bar (1,00 × 10 5Pa):

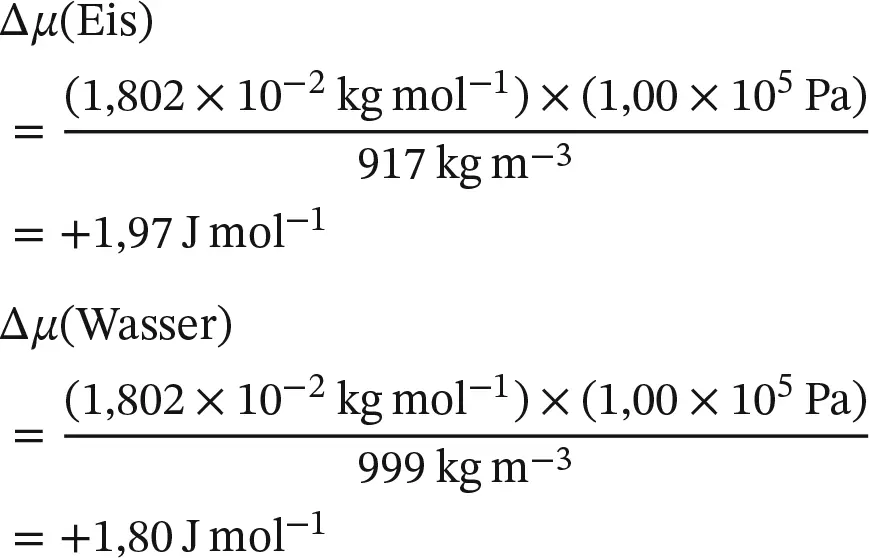
HinweisDas chemische Potenzial von Eis nimmt mit steigendem Druck schneller zu als das von Wasser; wenn sich beide Phasen bei 1 bar im Gleichgewicht befinden, schmilzt das Eis bei 2 bar.

Selbsttest 4.1

Wiederholen Sie die Rechnung für die feste und die flüssige Phase von Kohlendioxid (Molmasse 44,0 g mol −1), die sich miteinander im Gleichgewicht befinden. Gegeben sind die Dichten mit 2,35 g cm −3bzw. 2,50 g cm −3.

[Antwort: Δ μ (l) = + 1,87 J mol −1, Δ μ (s) = + 1,76 J mol −1; feste Phase wird gebildet.]

Wenn auf eine kondensierte Phase Druck ausgeübt wird, steigt ihr Dampfdruck, weil Moleküle aus ihr „heraus gedrückt“ werden und als Gas entweichen. Der erforderliche Druck kann mechanisch oder mithilfe eines unter Druck stehenden Inertgases ausgeübt werden ( Abb. 4.15); in letzterem Fall ist der Dampfdruck der Partialdruckder gasförmigen Phase, die sich mit der kondensierten Phase im Gleichgewicht befindet. In der folgenden Herleitung 4.2werden wir diesen Effekt thermodynamisch untersuchen und eine Beziehung zwischen dem ausgeübten Druck P und dem Dampfdruck p entwickeln.

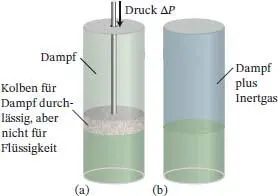
Abb. 4.15 Verschiedene Methoden, auf eine kondensierte Phase Druck auszuüben: (a) die kondensierte Phase selbst wird komprimiert, (b) der Druck wird durch ein Inertgas erzeugt. Mit steigendem Druck nimmt der Dampfdruck der kondensierten Phase zu.

Herleitung 4.2: Der Dampfdruck einer Flüssigkeit unter äußerem Druck

Zur Berechnung des Dampfdrucks einer unter Druck stehenden Flüssigkeit gehen wir davon aus, dass die chemischen Potenziale von flüssiger und gasförmiger Phase gleich sind: μ (l) = μ (g). Bei jeder Zustandsänderung, bei der das Gleichgewicht aufrecht erhalten wird, muss die Änderung von μ (l) genau der von μ (g) entsprechen: d μ (l) = d μ (g).

Schritt 1 Formulierung von Ausdrücken für die Änderungen der chemischen Potenziale aufgrund der Druckänderung .

Wenn der auf die Flüssigkeit wirkende Druck um d P zunimmt, ändert sich das chemische Potenzial dieser Phase um d μ (l) = V m(l) d P und das chemische Potenzial der Gasphase um d μ (g) = V m(g) d p . Dabei ist d p die Änderung des Drucks p der Gasphase, des Dampfdrucks, die wir berechnen wollen. Wenn wir für die Gasphase ideales Verhalten annehmen, können wir das molare Volumen durch V m(g) = R T / p ersetzen und erhalten d μ (g) = ( R T / p ) d p .

Schritt 2 Gleichsetzen der Änderungen der chemischen Potenziale von Dampf und Flüssigkeit .

Gleichsetzen der Änderungen der chemischen Potenziale beider Phasen (d μ (l) = V m(l) d P und d μ (g) = ( R T / p ) d p ) liefert

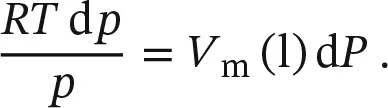
Achten Sie darauf, zwischen dem Gesamtdruck P und dem Partialdruck des Dampfs p zu unterscheiden. Wenn die Integrationsgrenzen benannt sind, können wir diesen Ausdruck leicht integrieren.

Schritt 3 Vorbereiten der Integration der Beziehung durch Identifizierung geeigneter Integrationsgrenzen .

Wenn auf die Flüssigkeit kein zusätzlicher Druck wirkt, entspricht ihr Druck P dem Dampfdruck p * unter Normalbedingungen; d. h. für P = p * gilt auch p = p *. Bei Anlegen eines zusätzlichen Drucks Δ P an die flüssige Phase wird deren Druck zu P = p + Δ P ; p ist der gesuchte Dampfdruck. Vorausgesetzt, der Dampfdruck hängt nur wenig vom äußeren Druck ab (was wir später nachweisen werden), kann man in dieser Gleichung p in guter Näherung durch p * ersetzen; die obere Integrationsgrenze ist damit p * + Δ P . Wir haben also folgende Integration vorzunehmen: