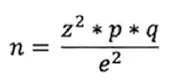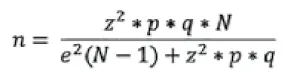Agustín Dousdebés Boada - ESTADÍSTICA APLICADA A PSICOLOGÍA Y EDUCACIÓN.

De la definición anterior hay algunas puntualizaciones clave a resaltar como son: “aceptar o rechazar relaciones hipotéticas” y “hacer inferencias fidedignas de observaciones empíricas”, esto refleja uno de los objetivos básicos de esta ciencia.

He citado algunas definiciones y las he colocado en orden cronológico para que el lector compare y según su criterio vea si considera ha existido o no una evolución en los conceptos de esta ciencia.

Se podría decir entonces que, sin que se tome esto como una definición específica, la Estadística es la ciencia que expresa en números los resultados de la observación objetiva del comportamiento de alguna variable a analizar, y con ellos trata de interpretar situaciones reales de dicho evento y como consecuencia propone conclusiones y sobre todo recomendaciones sobre el hecho investigado.

DIVISIÓN DE LA ESTADÍSTICA

La Estadística se divide en dos grandes estudios

1. Estadística Descriptiva: Su principal aporte es explicar lo que ocurre en un determinado grupo de estudio, puede valerse de tablas y gráficos que le ayuden a comprender mejor.

2. Estadística Inferencial: Su propósito es establecer inferencias o predicciones en base a los datos obtenidos de una población; permite ya relacionar variables y ayuda a tomar decisiones más específicas.

Para el estudio de cualquiera de ellas hay que aclarar que el proceso se basa en tomar cierta cantidad de datos que proporcionen información veraz y suficiente para analizar y darse una idea lo más cercana posible a la realidad específica de un grupo de estudio.

CONCEPTOS INICIALES

“El muestreo no es la simple sustitución de una cobertura parcial para una cobertura total. Muestreo es la ciencia y el arte de controlar y medir la fiabilidad de la información estadística útil a través de la teoría de la probabilidad”.

Deming (1950)

Población y muestra

Pero ¿cuál es esta realidad?, técnicamente la llamamos Población (universo) que será en definitiva la razón de nuestro estudio y para su análisis generalmente debemos tomar un cierto número de valores, que le llamaremos Muestra de tal manera que esta última cumpla con una condición fundamental: debe garantizar representatividad, por tanto tiene que reunir las mismas características de la población.

Debemos tomar en cuenta lo siguiente: todo subconjunto de la población es una muestra, pero no toda muestra es representativa, por tanto, para garantizar que el estudio tenga validez, se debe cumplir con la condición antes establecida; esto se trata de ejemplificar en la Figura 1.

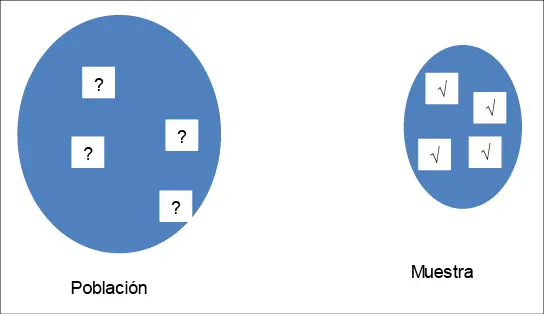
Figura 1: La muestra como un subconjunto de la población

Para efectos de proceso, la idea es la siguiente:

El investigador se hace preguntas sobre las características y comportamiento que puede tener una determinada población (objeto de estudio), para ello obtiene una muestra representativa y en ella realiza los estudios, obtiene resultados y hace conclusiones que permitan establecer, con determinada seguridad, que lo encontrado en la muestra ocurre también en la población.

Población

Es importante entonces establecer la población a la cual se va a dirigir un determinado estudio y para ello se debe delimitar con la mayor precisión posible cuál sería este grupo objetivo, es decir a qué conglomerado de personas va dirigida específicamente la investigación a realizar.

Para ello pongo los siguientes ejemplos comparativos sobre la identificación de la población objetivo:

1. Estudio del síndrome de Down.

2. Estudio del síndrome de Down en niños.

3. Estudio del síndrome de Down en niños de 4 a 8 años.

4. Estudio del síndrome de Down en niños de 4 a 8 años en establecimientos educativos.

5. Estudio del síndrome de Down en niños de 4 a 8 años en establecimientos educativos particulares.

6. Estudio del síndrome de Down en niños de 4 a 8 años en establecimientos educativos particulares de la zona norte.

7. Estudio del síndrome de Down en niños de 4 a 8 años en establecimientos educativos particulares de la zona norte de la ciudad de Quito.

Fíjese que en cada redacción se ha ido puntualizando la población objetivo, por ejemplo en el punto uno no se establece nada de hacia qué población va dirigido el estudio y en los sucesivos puntos se va aclarando cada vez mejor y determinando con mayor precisión la población en la que se va a realizar la investigación y a pesar de ello en algún momento del proceso el investigador debería establecer geográficamente cuál es esa “zona norte” (numeral 7).

Ahora bien, si ya se ha superado de la mejor manera este primer paso, ¿cuál es entonces la forma de obtener esos datos de la población que nos permita realizar un análisis fiable de ella? Para esto debemos referirnos a un segundo concepto muy importante en el ámbito de la Estadística, esto es la muestra y sus distintos métodos de encontrarla.

Muestra

Como se indicara en párrafos anteriores, la muestra es un subconjunto representativo de la población, esto significa que este grupo de datos deberá asegurar tener las mismas características del objetivo de estudio; por ejemplo si la población está conformada por hombres y mujeres, niños, adolescentes, personas mayores, etc., la muestra deberá reunir también a personas que representen a cada grupo, además, tomando en cuenta el mismo ejemplo, se deberá establecer la proporción de dichos elementos, es decir si hay un número muy grande de niños, esto deberá reflejarse proporcionalmente en la muestra.

Esta propiedad (la representatividad) es el requisito más importante que debe cumplir la muestra en referencia al universo de estudio.

Muestreo

¿Por qué tomar muestras? La principal razón es que normalmente los estudios e investigaciones se realizan en poblaciones muy grandes y por tanto es prácticamente imposible obtener datos de todos sus elementos.

El muestreo consiste en recopilar información confiable de una población utilizando técnicas que garanticen esta condición.

Para ello deben cumplirse requisitos como el número adecuado de datos, la idoneidad en la recopilación de los datos, garantizar que, para obtener los datos, no se haya realizado manipulación alguna, entre otros.

El establecer el número adecuado de datos depende de varios aspectos, entre ellos tenemos:

i. Cuánto margen de error se permite.

ii. Qué nivel de confianza se desea para el análisis (este tema se profundizará más adelante cuando se aborden temas referentes a la Estadística Inferencial).

iii. Si se considera que la población es finita o infinita.

Hay varias fórmulas a utilizar según el caso; las más utilizadas son las siguientes:

•Para poblaciones infinitas (más de 100.000 elementos):

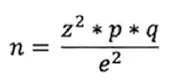
•Para poblaciones finitas (menos de 100.000 elementos, por tanto, es la fórmula más utilizada):

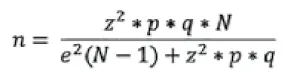
Explicación:

n = Número de elementos de la muestra a obtener

N = Número de elementos de la población

p y q = representan la probabilidad de que se presente un evento o también se dice que es la proporción en la que ocurre un evento y se ha establecido de antemano.

Para los valores de “p” y “q” se suele determinar igualdad, es decir: p = q = 0.5 esto es porque muy pocas veces se conoce la verdadera proporción en que ocurre un evento.