Daniel J. Duffy - Numerical Methods in Computational Finance

We now define another condition on the diffusion coefficient in Equation (3.17).

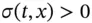C5: and for every 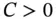there exists an 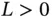and 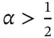such that:

Theorem 3.4Assume conditions C4, C1 and C5 hold. Then the Equation (3.17)has a continuous solution with probability 1 for any initial condition .

For proofs of these theorems, see Skorokhod (1982), for example.

In some cases it is possible to find a closed-form solution of Equation (3.17)(or equivalently, Equation (3.18)). When the drift and diffusion coefficients are constant, we see that the exact solution is given by the formula:

(3.19)

Knowing the exact solution is useful, because we can test the accuracy of finite difference schemes against it, and this gives us some insights into how well these schemes work for a range of parameter values.

It is useful to know how the solution of Equation (3.17)behaves for large values of time; the answer depends on a relationship between the drift and diffusion parameters:

In general it is not possible to find an exact solution, and in these cases we must resort to numerical approximation techniques.

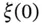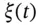Equation (3.17)is a one-factor equation because there is only one dependent variable (namely ) to be modelled. It is possible to define equations with several dependent variables. The prototypical non-linear stochastic differential equation is given by the system: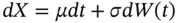

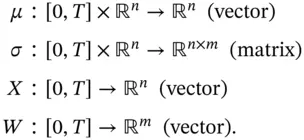
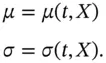
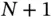(3.20)

where:

In general the drift and diffusion terms in (3.20)are non-linear:

This is a generalisation of Equation (3.17). Thus, instead of scalars this system employs vectors for the solution, drift and random number terms while the diffusion term is a rectangular matrix.

Existence and uniqueness theorems for the solution of the SDE system (3.20)are similar to those in the one-factor case. For example, theorem 5.2.1 in Øksendal (1998) addresses these issues. We discuss SDEs in more detail in Chapter 13.

In this section we introduce a class of one-step methods to approximate the solution of ODE system (3.1).

The first step is to replace continuous time by discrete time. To this end, we divide the interval [0, T ] into a number of subintervals. We define mesh points as follows: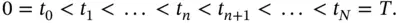

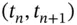In this case we define a set of subintervals of size , .

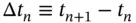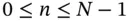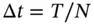In general, we speak of a non-uniform mesh when the sizes of the subintervals are not necessarily the same. However, in this book we consider in the main a class of finite difference schemes where the N subintervals have the same length (we then speak of a uniform mesh ), namely . The variable 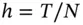is also used to denote the uniform mesh size .

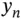In general, we define to be the approximate solution at time 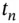and we write the functional dependence of 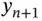on 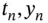and h by: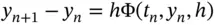

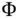(3.21)

where is called the increment function . For example, in the case of the explicit Euler method , this function is: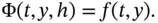

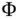The increment function represents the increment of the approximate solution. In general, the goal is to produce a formula for that agrees with a certain exact relative increment with an error of 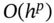where 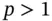without making it necessary to compute the derivative of f (Henrici (1962)). A special case of (3.21)is the fourth-order Runge–Kutta method :