(3) 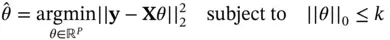
where 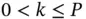 , and
, and 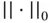 denotes the
denotes the 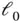 ‐norm, that is, the number of nonzero elements. Because best subset selection requires an immensely difficult nonconvex optimization, Tibshirani [38] famously replaces the
‐norm, that is, the number of nonzero elements. Because best subset selection requires an immensely difficult nonconvex optimization, Tibshirani [38] famously replaces the 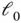 ‐norm with the
‐norm with the 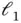 ‐norm, thereby providing sparsity, while nonetheless maintaining convexity.
‐norm, thereby providing sparsity, while nonetheless maintaining convexity.
Historically, Bayesians have paid much less attention to convexity than have optimization researchers. This is most likely because the basic theory [13] of MCMC does not require such restrictions: even if a target distribution has one million modes, the well‐constructed Markov chain explores them all in the limit. Despite these theoretical guarantees, a small literature has developed to tackle multimodal Bayesian inference [39–42] because multimodal target distributions do present a challenge in practice. In analogy with Equation (3), Bayesians seek to induce sparsity by specifiying priors such as the spike‐and‐slab [43–45], for example,
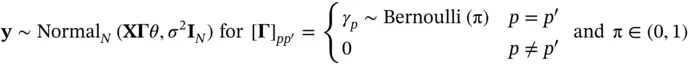
As with the best subset selection objective function, the spike‐and‐slab target distribution becomes heavily multimodal as 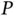 grows and the support of
grows and the support of  's discrete distribution grows to
's discrete distribution grows to 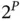 potential configurations.
potential configurations.
In the following section, we present an alternative Bayesian sparse regression approach that mitigates the combinatorial problem along with a state‐of‐the‐art computational technique that scales well both in 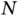 and
and 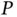 .
.
3 Model‐Specific Advances
These challenges will remain throughout the twenty‐first century, but it is possible to make significant advances for specific statistical tasks or classes of models. Section 3.1considers Bayesian sparse regression based on continuous shrinkage priors, designed to alleviate the heavy multimodality (big 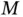 ) of the more traditional spike‐and‐slab approach. This model presents a major computational challenge as
) of the more traditional spike‐and‐slab approach. This model presents a major computational challenge as 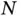 and
and 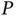 grow, but a recent computational advance makes the posterior inference feasible for many modern large‐scale applications.
grow, but a recent computational advance makes the posterior inference feasible for many modern large‐scale applications.
And because of the rise of data science, there are increasing opportunities for computational statistics to grow by enabling and extending statistical inference for scientific applications previously outside of mainstream statistics. Here, the science may dictate the development of structured models with complexity possibly growing in  and
and 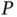 . Section 3.2presents a method for fast phylogenetic inference, where the primary structure of interest is a “family tree” describing a biological evolutionary history.
. Section 3.2presents a method for fast phylogenetic inference, where the primary structure of interest is a “family tree” describing a biological evolutionary history.
3.1 Bayesian Sparse Regression in the Age of Big N and Big P
With the goal of identifying a small subset of relevant features among a large number of potential candidates, sparse regression techniques have long featured in a range of statistical and data science applications [46]. Traditionally, such techniques were commonly applied in the “ 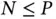 ” setting, and correspondingly computational algorithms focused on this situation [47], especially within the Bayesian literature [48].
” setting, and correspondingly computational algorithms focused on this situation [47], especially within the Bayesian literature [48].
Due to a growing number of initiatives for large‐scale data collections and new types of scientific inquiries made possible by emerging technologies, however, increasingly common are datasets that are “big 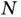 ” and “big
” and “big 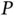 ” at the same time. For example, modern observational studies using health‐care databases routinely involve
” at the same time. For example, modern observational studies using health‐care databases routinely involve 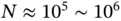 patients and
patients and 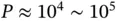 clinical covariates [49]. The UK Biobank provides brain imaging data on
clinical covariates [49]. The UK Biobank provides brain imaging data on 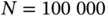 patients, with
patients, with 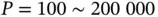 , depending on the scientific question of interests [50]. Single‐cell RNA sequencing can generate datasets with
, depending on the scientific question of interests [50]. Single‐cell RNA sequencing can generate datasets with 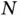 (the number of cells) in millions and
(the number of cells) in millions and  (the number of genes) in tens of thousands, with the trend indicating further growths in data size to come [51].
(the number of genes) in tens of thousands, with the trend indicating further growths in data size to come [51].
3.1.1 Continuous shrinkage: alleviating big M
Bayesian sparse regression, despite its desirable theoretical properties and flexibility to serve as a building block for richer statistical models, has always been relatively computationally intensive even before the advent of “big 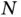 and big
and big 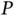 ” data [45, 52, 53]. A major source of its computational burden is severe posterior multimodality (big
” data [45, 52, 53]. A major source of its computational burden is severe posterior multimodality (big 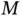 ) induced by the discrete binary nature of spike‐and‐slab priors ( Section 2.3). The class of global–local continuous shrinkage priors is a more recent alternative to shrink
) induced by the discrete binary nature of spike‐and‐slab priors ( Section 2.3). The class of global–local continuous shrinkage priors is a more recent alternative to shrink 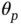 s in a more continuous manner, thereby alleviating (if not eliminating) the multimodality issue [54, 55]. This class of prior is represented as a scale mixture of Gaussians:
s in a more continuous manner, thereby alleviating (if not eliminating) the multimodality issue [54, 55]. This class of prior is represented as a scale mixture of Gaussians:
Читать дальше

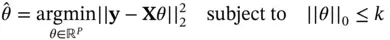
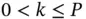 , and
, and 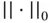 denotes the
denotes the 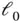 ‐norm, that is, the number of nonzero elements. Because best subset selection requires an immensely difficult nonconvex optimization, Tibshirani [38] famously replaces the
‐norm, that is, the number of nonzero elements. Because best subset selection requires an immensely difficult nonconvex optimization, Tibshirani [38] famously replaces the 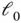 ‐norm with the
‐norm with the 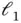 ‐norm, thereby providing sparsity, while nonetheless maintaining convexity.
‐norm, thereby providing sparsity, while nonetheless maintaining convexity.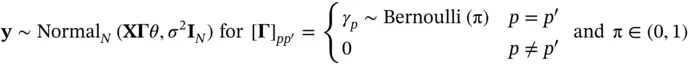
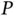 grows and the support of
grows and the support of  's discrete distribution grows to
's discrete distribution grows to 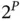 potential configurations.
potential configurations.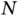 and
and 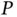 .
.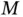 ) of the more traditional spike‐and‐slab approach. This model presents a major computational challenge as
) of the more traditional spike‐and‐slab approach. This model presents a major computational challenge as 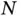 and
and 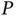 grow, but a recent computational advance makes the posterior inference feasible for many modern large‐scale applications.
grow, but a recent computational advance makes the posterior inference feasible for many modern large‐scale applications. and
and 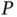 . Section 3.2presents a method for fast phylogenetic inference, where the primary structure of interest is a “family tree” describing a biological evolutionary history.
. Section 3.2presents a method for fast phylogenetic inference, where the primary structure of interest is a “family tree” describing a biological evolutionary history.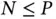 ” setting, and correspondingly computational algorithms focused on this situation [47], especially within the Bayesian literature [48].
” setting, and correspondingly computational algorithms focused on this situation [47], especially within the Bayesian literature [48].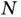 ” and “big
” and “big 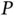 ” at the same time. For example, modern observational studies using health‐care databases routinely involve
” at the same time. For example, modern observational studies using health‐care databases routinely involve 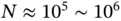 patients and
patients and 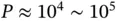 clinical covariates [49]. The UK Biobank provides brain imaging data on
clinical covariates [49]. The UK Biobank provides brain imaging data on 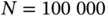 patients, with
patients, with 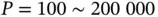 , depending on the scientific question of interests [50]. Single‐cell RNA sequencing can generate datasets with
, depending on the scientific question of interests [50]. Single‐cell RNA sequencing can generate datasets with 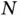 (the number of cells) in millions and
(the number of cells) in millions and  (the number of genes) in tens of thousands, with the trend indicating further growths in data size to come [51].
(the number of genes) in tens of thousands, with the trend indicating further growths in data size to come [51].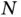 and big
and big  ” data [45, 52, 53]. A major source of its computational burden is severe posterior multimodality (big
” data [45, 52, 53]. A major source of its computational burden is severe posterior multimodality (big 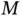 ) induced by the discrete binary nature of spike‐and‐slab priors ( Section 2.3). The class of global–local continuous shrinkage priors is a more recent alternative to shrink
) induced by the discrete binary nature of spike‐and‐slab priors ( Section 2.3). The class of global–local continuous shrinkage priors is a more recent alternative to shrink 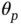 s in a more continuous manner, thereby alleviating (if not eliminating) the multimodality issue [54, 55]. This class of prior is represented as a scale mixture of Gaussians:
s in a more continuous manner, thereby alleviating (if not eliminating) the multimodality issue [54, 55]. This class of prior is represented as a scale mixture of Gaussians:![Роман Зыков - Роман с Data Science. Как монетизировать большие данные [litres]](/books/438007/roman-zykov-roman-s-data-science-kak-monetizirova-thumb.webp)










