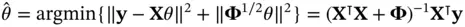
For illustrative purposes, we consider the following direct method for computing  . 4 We can first multiply the
. 4 We can first multiply the  design matrix
design matrix  by its transpose at the cost of
by its transpose at the cost of 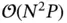 and subsequently invert the
and subsequently invert the 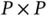 matrix
matrix 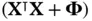 at the cost of
at the cost of  . The total
. The total 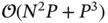 complexity shows that (i) a large number of parameters is often sufficient for making even the simplest of tasks infeasible and (ii) a moderate number of parameters can render a task impractical when there are a large number of observations. These two insights extend to more complicated models: the same complexity analysis holds for the fitting of generalized linear models (GLMs) as described in McCullagh and Nelder [12].
complexity shows that (i) a large number of parameters is often sufficient for making even the simplest of tasks infeasible and (ii) a moderate number of parameters can render a task impractical when there are a large number of observations. These two insights extend to more complicated models: the same complexity analysis holds for the fitting of generalized linear models (GLMs) as described in McCullagh and Nelder [12].
In the context of Bayesian inference, the length 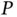 of the vector
of the vector 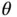 dictates the dimension of the MCMC state space. For the M‐H algorithm ( Section 2.1) with
dictates the dimension of the MCMC state space. For the M‐H algorithm ( Section 2.1) with 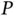 ‐dimensional Gaussian target and proposal, Gelman et al . [25] show that the proposal distribution's covariance should be scaled by a factor inversely proportional to
‐dimensional Gaussian target and proposal, Gelman et al . [25] show that the proposal distribution's covariance should be scaled by a factor inversely proportional to 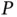 . Hence, as the dimension of the state space grows, it behooves one to propose states
. Hence, as the dimension of the state space grows, it behooves one to propose states 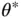 that are closer to the current state of the Markov chain, and one must greatly increase the number
that are closer to the current state of the Markov chain, and one must greatly increase the number 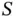 of MCMC iterations. At the same time, an increasing
of MCMC iterations. At the same time, an increasing  often slows down rate‐limiting likelihood calculations ( Section 2.1). Taken together, one must generate many more, much slower MCMC iterations. The wide applicability of latent variable models [26] ( Sections 3.1and 3.2) for which each observation has its own parameter set (e.g.,
often slows down rate‐limiting likelihood calculations ( Section 2.1). Taken together, one must generate many more, much slower MCMC iterations. The wide applicability of latent variable models [26] ( Sections 3.1and 3.2) for which each observation has its own parameter set (e.g., 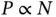 ) means M‐H simply does not work for a huge class of models popular with practitioners.
) means M‐H simply does not work for a huge class of models popular with practitioners.
For these reasons, Hamiltonian Monte Carlo (HMC) [27] has become a popular algorithm for fitting Bayesian models with large numbers of parameters. Like M‐H, HMC uses an accept step ( Equation 2). Unlike M‐H, HMC takes advantage of additional information about the target distribution in the form of the log‐posterior gradient. HMC works by doubling the state space dimension with an auxiliary Gaussian “momentum” variable 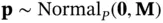 independent to the “position” variable
independent to the “position” variable 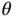 . The constructed Hamiltonian system has energy function given by the negative logarithm of the joint distribution
. The constructed Hamiltonian system has energy function given by the negative logarithm of the joint distribution
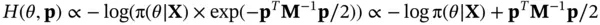
and we produce proposals by simulating the system according to Hamilton's equations
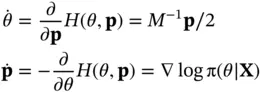
Thus, the momentum of the system moves in the direction of the steepest ascent for the log‐posterior, forming an analogy with first‐order optimization. The cost is repeated gradient evaluations that may comprise a new computational bottleneck, but the result is effective MCMC for tens of thousands of parameters [21, 28]. The success of HMC has inspired research into other methods leveraging gradient information to generate better MCMC proposals when 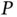 is large [29].
is large [29].
Global optimization, or the problem of finding the minimum of a function with arbitrarily many local minima, is NP‐complete in general [30], meaning – in layman's terms – it is impossibly hard. In the absence of a tractable theory, by which one might prove one's global optimization procedure works, brute‐force grid and random searches and heuristic methods such as particle swarm optimization [31] and genetic algorithms [32] have been popular. Due to the overwhelming difficulty of global optimization, a large portion of the optimization literature has focused on the particularly well‐behaved class of convex functions [33, 34], which do not admit multiple local minima. Since Fisher introduced his “maximum likelihood” in 1922 [35], statisticians have thought in terms of maximization, but convexity theory still applies by a trivial negation of the objective function. Nonetheless, most statisticians safely ignored concavity during the twentieth century: exponential family log‐likelihoods are log‐concave, so Newton–Raphson and Fisher scoring are guaranteed optimality in the context of GLMs [12, 34].
Nearing the end of the twentieth century, multimodality and nonconvexity became more important for statisticians considering high‐dimensional regression, that is, regression with many covariates (big 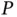 ). Here, for purposes of interpretability and variance reduction, one would like to induce sparsity on the weights vector
). Here, for purposes of interpretability and variance reduction, one would like to induce sparsity on the weights vector  by performing best subset selection [36, 37]:
by performing best subset selection [36, 37]:
Читать дальше

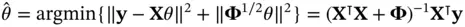
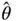 . 4 We can first multiply the
. 4 We can first multiply the 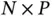 design matrix
design matrix  by its transpose at the cost of
by its transpose at the cost of 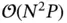 and subsequently invert the
and subsequently invert the 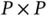 matrix
matrix 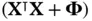 at the cost of
at the cost of 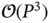 . The total
. The total 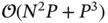 complexity shows that (i) a large number of parameters is often sufficient for making even the simplest of tasks infeasible and (ii) a moderate number of parameters can render a task impractical when there are a large number of observations. These two insights extend to more complicated models: the same complexity analysis holds for the fitting of generalized linear models (GLMs) as described in McCullagh and Nelder [12].
complexity shows that (i) a large number of parameters is often sufficient for making even the simplest of tasks infeasible and (ii) a moderate number of parameters can render a task impractical when there are a large number of observations. These two insights extend to more complicated models: the same complexity analysis holds for the fitting of generalized linear models (GLMs) as described in McCullagh and Nelder [12].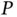 of the vector
of the vector 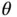 dictates the dimension of the MCMC state space. For the M‐H algorithm ( Section 2.1) with
dictates the dimension of the MCMC state space. For the M‐H algorithm ( Section 2.1) with  ‐dimensional Gaussian target and proposal, Gelman et al . [25] show that the proposal distribution's covariance should be scaled by a factor inversely proportional to
‐dimensional Gaussian target and proposal, Gelman et al . [25] show that the proposal distribution's covariance should be scaled by a factor inversely proportional to 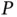 . Hence, as the dimension of the state space grows, it behooves one to propose states
. Hence, as the dimension of the state space grows, it behooves one to propose states 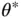 that are closer to the current state of the Markov chain, and one must greatly increase the number
that are closer to the current state of the Markov chain, and one must greatly increase the number 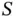 of MCMC iterations. At the same time, an increasing
of MCMC iterations. At the same time, an increasing  often slows down rate‐limiting likelihood calculations ( Section 2.1). Taken together, one must generate many more, much slower MCMC iterations. The wide applicability of latent variable models [26] ( Sections 3.1and 3.2) for which each observation has its own parameter set (e.g.,
often slows down rate‐limiting likelihood calculations ( Section 2.1). Taken together, one must generate many more, much slower MCMC iterations. The wide applicability of latent variable models [26] ( Sections 3.1and 3.2) for which each observation has its own parameter set (e.g., 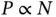 ) means M‐H simply does not work for a huge class of models popular with practitioners.
) means M‐H simply does not work for a huge class of models popular with practitioners.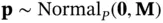 independent to the “position” variable
independent to the “position” variable 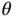 . The constructed Hamiltonian system has energy function given by the negative logarithm of the joint distribution
. The constructed Hamiltonian system has energy function given by the negative logarithm of the joint distribution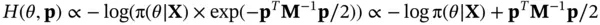
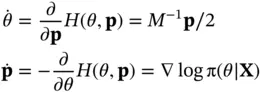
 is large [29].
is large [29]. ). Here, for purposes of interpretability and variance reduction, one would like to induce sparsity on the weights vector
). Here, for purposes of interpretability and variance reduction, one would like to induce sparsity on the weights vector  by performing best subset selection [36, 37]:
by performing best subset selection [36, 37]:![Роман Зыков - Роман с Data Science. Как монетизировать большие данные [litres]](/books/438007/roman-zykov-roman-s-data-science-kak-monetizirova-thumb.webp)










