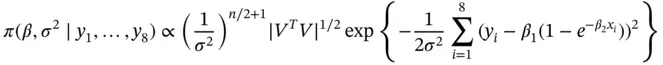
The goal is to estimate the posterior mean of 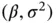 . We implement an MCMC algorithm to estimate the posterior mean and implement the relative‐standard deviation sequential stopping rule via effective sample size.
. We implement an MCMC algorithm to estimate the posterior mean and implement the relative‐standard deviation sequential stopping rule via effective sample size.
We sample from the posterior distribution via a componentwise random walk Metropolis–Hastings algorithm updating 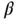 first and then
first and then 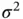 , with step size for both components chosen so that the acceptance probability is around 30%. Since the posterior distribution is three‐dimensional, the minimum ESS required for
, with step size for both components chosen so that the acceptance probability is around 30%. Since the posterior distribution is three‐dimensional, the minimum ESS required for 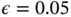 and
and 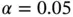 in Equation ( 7) is 8123. Thus, we first run the sampler for
in Equation ( 7) is 8123. Thus, we first run the sampler for 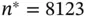 and obtain early estimates of
and obtain early estimates of 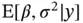 and the corresponding effective sample size. We then proceed to run the sampler until ESS nusing
and the corresponding effective sample size. We then proceed to run the sampler until ESS nusing 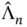 and
and 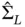 with
with 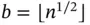 in Equation ( 4) is more than 8123.
in Equation ( 4) is more than 8123.
At 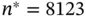 , ESS nwas 237, and the estimated density plot is presented in Figure 3by the dashed line. We verify the termination criteria in Equation ( 7) incrementally, and simulation terminates at
, ESS nwas 237, and the estimated density plot is presented in Figure 3by the dashed line. We verify the termination criteria in Equation ( 7) incrementally, and simulation terminates at 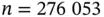 iterations. The final estimated density is presented in Figure 3by the solid line.
iterations. The final estimated density is presented in Figure 3by the solid line.
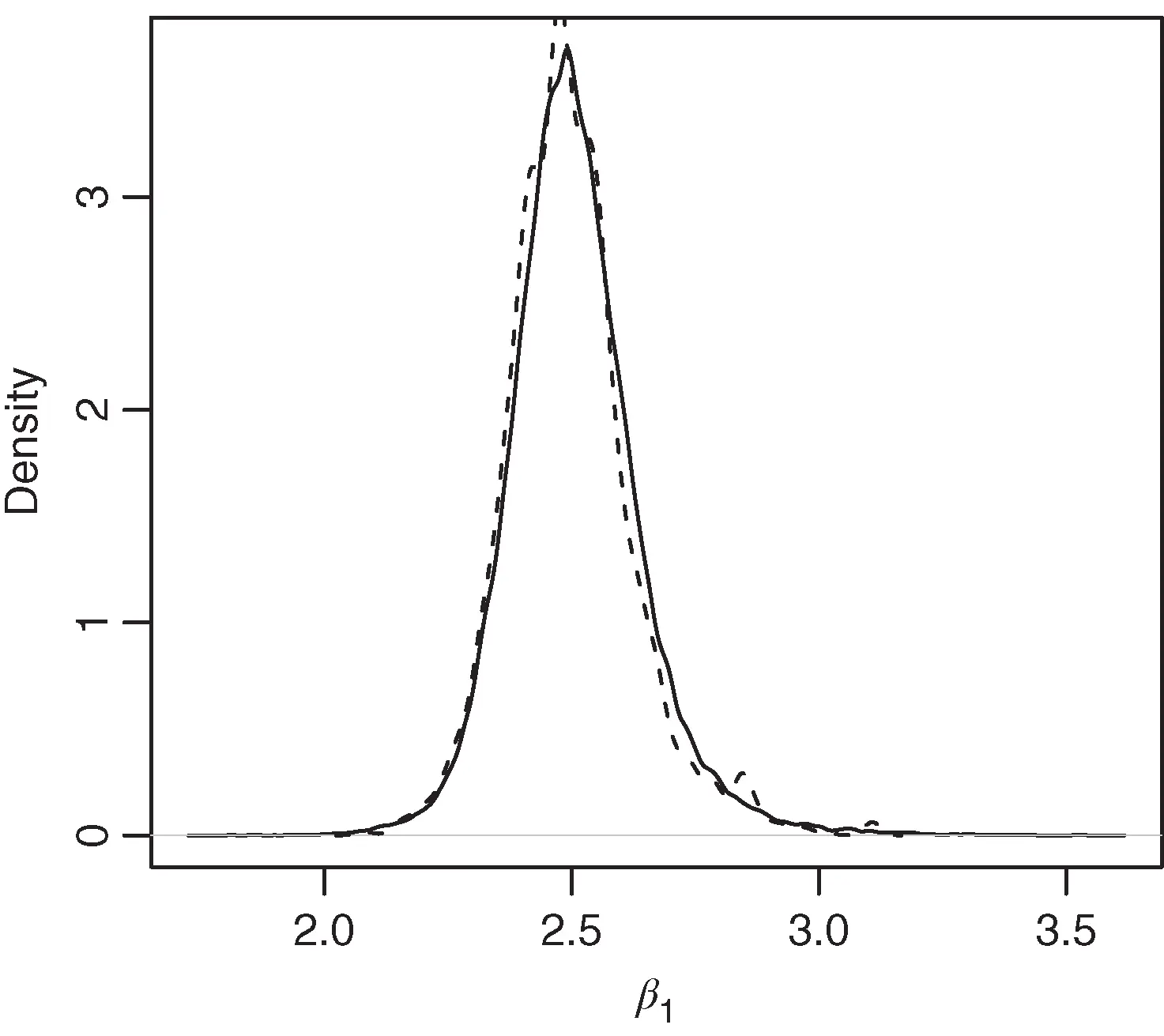
Figure 3 Estimated density of the marginal posterior for 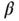 from an initial run of
from an initial run of 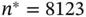 (dashed) and at termination (solid).
(dashed) and at termination (solid).
At termination, the estimated posterior mean is 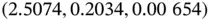 , and 80% credible intervals are
, and 80% credible intervals are 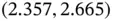 ,
,  , and
, and 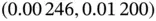 for
for 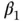 ,
, 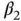 , and
, and 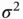 , respectively.
, respectively.
It is possible to run a more efficient linchpin sampler [42] by integrating out 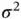 from the posterior. That is,
from the posterior. That is,  , where
, where
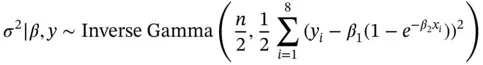
and
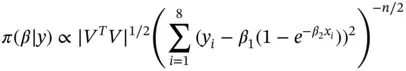
The sampler then proceeds to implement a random walk Metropolis–Hastings step to update 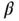 , and a draw from
, and a draw from 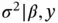 yields a joint MCMC draw from the posterior. We empirically note that this linchpin variable sampler yields lower marginal autocorrelation in
yields a joint MCMC draw from the posterior. We empirically note that this linchpin variable sampler yields lower marginal autocorrelation in 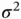 as illustrated by Figure 4.
as illustrated by Figure 4.
Repeating the previous procedure with the linchpin sampler, we have an estimated ESS at 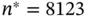 of 652, and the sequential stopping rule terminates at
of 652, and the sequential stopping rule terminates at 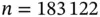 . The resulting estimates of posterior mean and quantiles are similar. Thus, using a more efficient sampler requires substantially fewer iterations to obtain estimates of similar quality.
. The resulting estimates of posterior mean and quantiles are similar. Thus, using a more efficient sampler requires substantially fewer iterations to obtain estimates of similar quality.
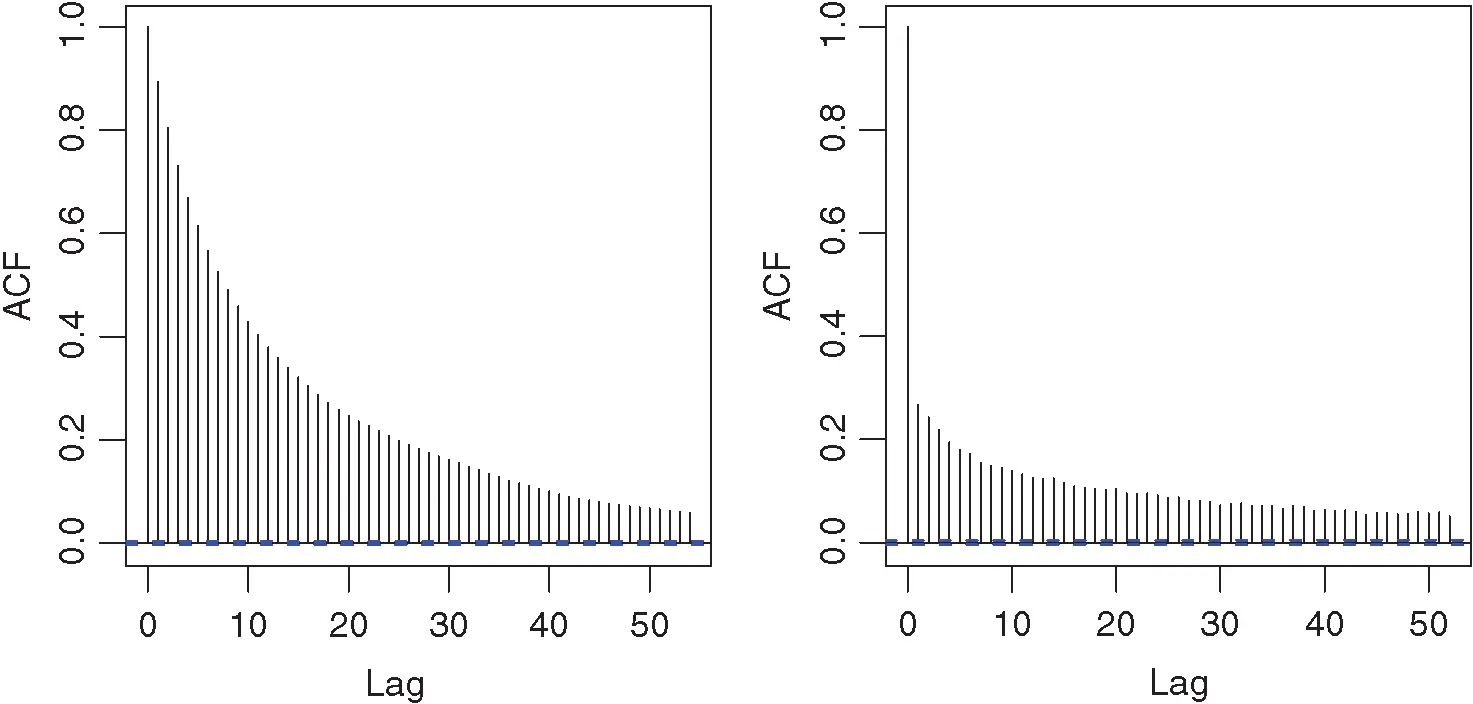
Figure 4 Estimated autocorrelations for nonlinchpin sampler (a) and linchpin sampler (b).
1For constructing simultaneous confidence intervals with approximately correct coverage, see Robertson et al. [10].
1 1 Caffo, B.S., Booth, J.G., and Davison, A.C. (2002) Empirical sup rejection sampling. Biometrika, 89, 745–754.
2 2 Chib, S. and Greenberg, E. (1995) Understanding the Metropolis‐Hastings algorithm. Am. Stat., 49, 327–335.
Читать дальше

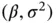 . We implement an MCMC algorithm to estimate the posterior mean and implement the relative‐standard deviation sequential stopping rule via effective sample size.
. We implement an MCMC algorithm to estimate the posterior mean and implement the relative‐standard deviation sequential stopping rule via effective sample size.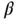 first and then
first and then 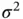 , with step size for both components chosen so that the acceptance probability is around 30%. Since the posterior distribution is three‐dimensional, the minimum ESS required for
, with step size for both components chosen so that the acceptance probability is around 30%. Since the posterior distribution is three‐dimensional, the minimum ESS required for 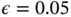 and
and 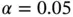 in Equation ( 7) is 8123. Thus, we first run the sampler for
in Equation ( 7) is 8123. Thus, we first run the sampler for 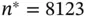 and obtain early estimates of
and obtain early estimates of 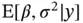 and the corresponding effective sample size. We then proceed to run the sampler until ESS nusing
and the corresponding effective sample size. We then proceed to run the sampler until ESS nusing 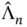 and
and 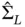 with
with 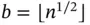 in Equation ( 4) is more than 8123.
in Equation ( 4) is more than 8123.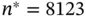 , ESS nwas 237, and the estimated density plot is presented in Figure 3by the dashed line. We verify the termination criteria in Equation ( 7) incrementally, and simulation terminates at
, ESS nwas 237, and the estimated density plot is presented in Figure 3by the dashed line. We verify the termination criteria in Equation ( 7) incrementally, and simulation terminates at 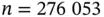 iterations. The final estimated density is presented in Figure 3by the solid line.
iterations. The final estimated density is presented in Figure 3by the solid line.
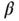 from an initial run of
from an initial run of 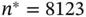 (dashed) and at termination (solid).
(dashed) and at termination (solid).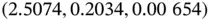 , and 80% credible intervals are
, and 80% credible intervals are 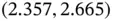 ,
,  , and
, and 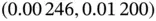 for
for 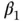 ,
, 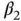 , and
, and 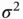 , respectively.
, respectively.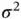 from the posterior. That is,
from the posterior. That is,  , where
, where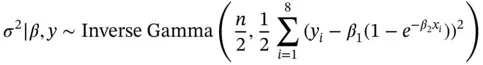
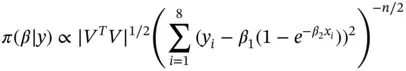
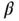 , and a draw from
, and a draw from 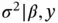 yields a joint MCMC draw from the posterior. We empirically note that this linchpin variable sampler yields lower marginal autocorrelation in
yields a joint MCMC draw from the posterior. We empirically note that this linchpin variable sampler yields lower marginal autocorrelation in 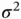 as illustrated by Figure 4.
as illustrated by Figure 4.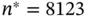 of 652, and the sequential stopping rule terminates at
of 652, and the sequential stopping rule terminates at 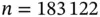 . The resulting estimates of posterior mean and quantiles are similar. Thus, using a more efficient sampler requires substantially fewer iterations to obtain estimates of similar quality.
. The resulting estimates of posterior mean and quantiles are similar. Thus, using a more efficient sampler requires substantially fewer iterations to obtain estimates of similar quality.
![Роман Зыков - Роман с Data Science. Как монетизировать большие данные [litres]](/books/438007/roman-zykov-roman-s-data-science-kak-monetizirova-thumb.webp)










