Computational Statistics in Data Science
Здесь есть возможность читать онлайн «Computational Statistics in Data Science» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Computational Statistics in Data Science
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Computational Statistics in Data Science: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Computational Statistics in Data Science»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Computational Statistics in Data Science
Computational Statistics in Data Science
Wiley StatsRef: Statistics Reference Online
Computational Statistics in Data Science

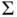 is larger
is larger 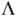 . This naturally implies that MCMC simulations require more samples than IID simulations. Using Theorem 1to assess the simulation reliability requires estimation of
. This naturally implies that MCMC simulations require more samples than IID simulations. Using Theorem 1to assess the simulation reliability requires estimation of 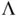 and
and 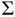 , which we describe in Section 4.
, which we describe in Section 4.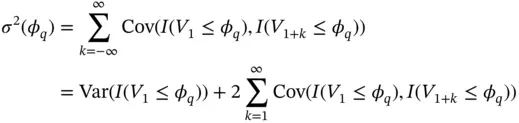
 be absolutely continuous, twice differentiable with density
be absolutely continuous, twice differentiable with density 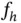 , and let
, and let 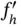 be bounded within some neighborhood of
be bounded within some neighborhood of  .
.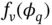 , can be estimated using a Gaussian kernel density estimator. In addition,
, can be estimated using a Gaussian kernel density estimator. In addition, 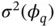 is replaced with
is replaced with  , the univariate version of
, the univariate version of 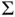 for
for 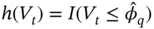 . We present methods of estimating
. We present methods of estimating 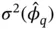 in Section 4.
in Section 4.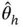 and a delta method argument yields an elementwise asymptotic distribution of
and a delta method argument yields an elementwise asymptotic distribution of 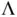 . Let
. Let 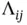 denote the
denote the 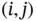 th element of
th element of 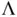 . If
. If 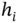 and
and 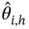 denote the components of
denote the components of 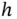 and
and 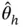 , respectively, then the
, respectively, then the 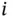 th diagonal of
th diagonal of 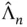 is
is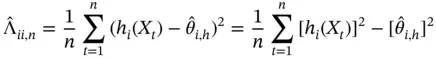
 . A similar argument can be made for the off‐diagonals of
. A similar argument can be made for the off‐diagonals of  . Under the conditions of Theorem 1,
. Under the conditions of Theorem 1,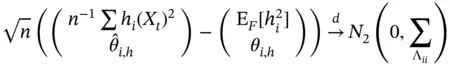
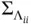 is
is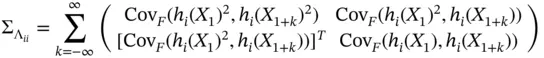
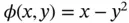 , we obtain
, we obtain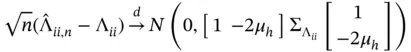
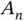 is an estimate of the limiting Monte Carlo variance–covariance matrix,
is an estimate of the limiting Monte Carlo variance–covariance matrix, 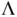 for IID sampling, and
for IID sampling, and 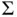 for MCMC sampling. Let
for MCMC sampling. Let 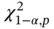 be the
be the 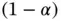 ‐quantile of a
‐quantile of a 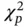 distribution. The CLT yields a large‐sample confidence region around
distribution. The CLT yields a large‐sample confidence region around  as
as![Роман Зыков - Роман с Data Science. Как монетизировать большие данные [litres]](/books/438007/roman-zykov-roman-s-data-science-kak-monetizirova-thumb.webp)










