Computational Statistics in Data Science

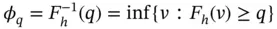
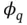Sample statistics are used to estimate . That is, let 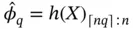be the th order statistic of . Then, standard arguments for IID sampling and MCMC [11] show that 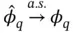as .

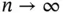Other quantities of interest that cannot naturally be presented as expectations (i.e., coefficient of variation) can be estimated by standard plug‐in estimation techniques. We focus on estimating the variance–covariance matrix of under

A natural estimator is the sample covariance matrix

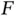
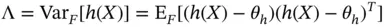
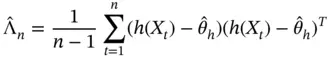
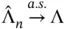The strong law of large numbers and the continuous mapping theorem imply that as 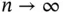. For IID samples, 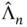is unbiased, but for MCMC samples under stationarity, 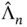is typically biased from below [12]

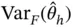For MCMC samples, is typically larger than 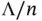, yielding biased‐from‐below estimation. If obtaining an unbiased estimator of 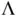is desirable, a bias correction should be done by estimating Var using methods described in Section 4.

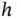An asymptotic sampling distribution for estimators in the previous section can be used to summarize the Monte Carlo variability, provided it is available and the limiting variance is estimable. For IID sampling, moment conditions for the function of interest, , with respect to the target distribution, 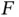, suffice. For MCMC sampling, more care needs to be taken to ensure that a limiting distribution holds. We present a subset of the conditions under which the estimators exhibit a normal limiting distribution [9, 13]. The main Markov chain assumption is that of polynomial ergodicity . Let 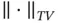denote the total‐variation distance. Let 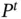be the ‐step Markov chain transition kernel, and let 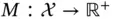such that 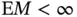and for ,

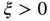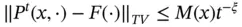
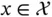for all . The constant 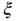dictates the rate of convergence of the Markov chain. Ergodic Markov chains on finite state spaces are polynomially ergodic. On general state spaces, demonstrating at least polynomial ergodicity usually requires a separate study of the sampler, and we provide some references in Section 6.

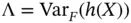Recall that . For MCMC sampling, a key quantity of interest will be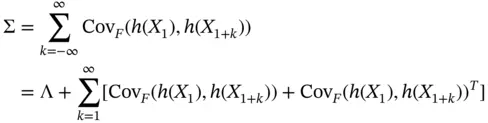

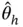which we assume is positive‐definite. A CLT for a Monte Carlo average, , is available under both IID and MCMC sampling.

1 IID. Let . If , then, as ,

2 MCMC. Let be polynomially ergodic of order where such that , then if is positive‐definite, as ,