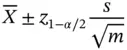
Confidence intervals are notoriously difficult to understand at a first instance, and thus a standard Monte Carlo experiment in an introductory statistics course is that of repeating the above experiment multiple times and illustrating that on average about 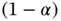 proportion of such confidence intervals will contain the true mean. That is, for
proportion of such confidence intervals will contain the true mean. That is, for 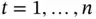 , we generate
, we generate  , calculate the mean
, calculate the mean 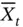 and the sample variance
and the sample variance 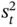 , and define
, and define 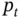 to be
to be
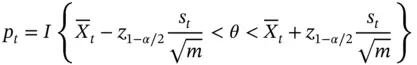
where 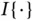 is the indicator function. By the law of large numbers,
is the indicator function. By the law of large numbers, 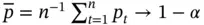 with probability 1, as
with probability 1, as 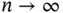 , and the following CLT holds:
, and the following CLT holds:
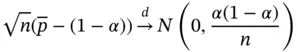
In conducting this experiment, we must choose the Monte Carlo sample size 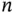 . A reasonable argument here is that our estimator
. A reasonable argument here is that our estimator 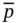 must be accurate up to the second significant digit with roundoff. That is, we may allow a margin of error of 0.005. This implies that
must be accurate up to the second significant digit with roundoff. That is, we may allow a margin of error of 0.005. This implies that 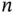 must be chosen so that
must be chosen so that
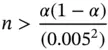
That is, to construct, say a 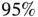 confidence interval, an accurate Monte Carlo study in this simple example requires at least 1900 Monte Carlo samples. A higher precision would require an even larger simulation size! This is an example of an absolute precision stopping rule ( Section 5) and is unique since the limiting variance is known. For further discussion of this example, see Frey [8].
confidence interval, an accurate Monte Carlo study in this simple example requires at least 1900 Monte Carlo samples. A higher precision would require an even larger simulation size! This is an example of an absolute precision stopping rule ( Section 5) and is unique since the limiting variance is known. For further discussion of this example, see Frey [8].
Recall that  is a
is a 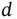 ‐dimensional target distribution, and interest is in estimating different features of
‐dimensional target distribution, and interest is in estimating different features of 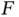 . In Monte Carlo simulation, we generate
. In Monte Carlo simulation, we generate 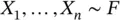 either via IID sampling or via a Markov chain that has
either via IID sampling or via a Markov chain that has  as its limiting distribution. For MCMC samples, we assume throughout that a Harris ergodic Markov chain is employed ensuring convergence of sample statistics to (finite) population quantities (see Roberts and Rosenthal [9], for definitions).
as its limiting distribution. For MCMC samples, we assume throughout that a Harris ergodic Markov chain is employed ensuring convergence of sample statistics to (finite) population quantities (see Roberts and Rosenthal [9], for definitions).
The most common quantity of interest in Monte Carlo simulations is the expectation of a function of the target distribution. Let 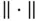 denote the Euclidean norm, and let
denote the Euclidean norm, and let 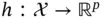 , so that interest is in estimating
, so that interest is in estimating
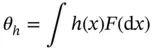
where we assume 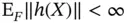 . If
. If 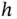 is identity, then the mean of the target is of interest. Alternatively,
is identity, then the mean of the target is of interest. Alternatively, 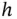 can be chosen so that moments or other quantities are of interest. A Monte Carlo estimator of
can be chosen so that moments or other quantities are of interest. A Monte Carlo estimator of  is
is
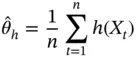
For IID and MCMC sampling, the ergodic theorem implies that 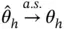 as
as 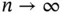 . The Monte Carlo average
. The Monte Carlo average 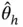 is naturally unbiased as long as the samples are either IID or the Markov chain is stationary.
is naturally unbiased as long as the samples are either IID or the Markov chain is stationary.
Quantiles are particularly of interest when making credible intervals in Bayesian posterior distributions or making boxplots from Monte Carlo simulations. In this section, we assume that 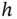 is one‐dimensional (i.e.,
is one‐dimensional (i.e., 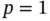 ). Extensions to
). Extensions to 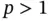 are straightforward but notationally involved [10]. For
are straightforward but notationally involved [10]. For 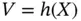 , interest may be in estimating a quantile of
, interest may be in estimating a quantile of 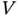 . Let
. Let 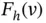 be the distribution function of
be the distribution function of 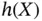 , assumed to be absolutely continuous with a continuous density
, assumed to be absolutely continuous with a continuous density 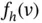 . The
. The 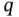 ‐quantile associated with
‐quantile associated with 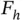 is
is
Читать дальше

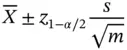
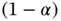 proportion of such confidence intervals will contain the true mean. That is, for
proportion of such confidence intervals will contain the true mean. That is, for 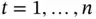 , we generate
, we generate  , calculate the mean
, calculate the mean 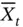 and the sample variance
and the sample variance 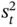 , and define
, and define 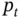 to be
to be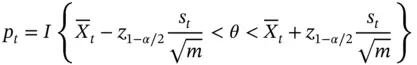
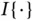 is the indicator function. By the law of large numbers,
is the indicator function. By the law of large numbers, 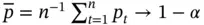 with probability 1, as
with probability 1, as 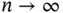 , and the following CLT holds:
, and the following CLT holds: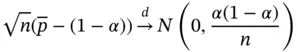
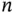 . A reasonable argument here is that our estimator
. A reasonable argument here is that our estimator 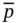 must be accurate up to the second significant digit with roundoff. That is, we may allow a margin of error of 0.005. This implies that
must be accurate up to the second significant digit with roundoff. That is, we may allow a margin of error of 0.005. This implies that 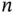 must be chosen so that
must be chosen so that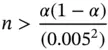
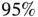 confidence interval, an accurate Monte Carlo study in this simple example requires at least 1900 Monte Carlo samples. A higher precision would require an even larger simulation size! This is an example of an absolute precision stopping rule ( Section 5) and is unique since the limiting variance is known. For further discussion of this example, see Frey [8].
confidence interval, an accurate Monte Carlo study in this simple example requires at least 1900 Monte Carlo samples. A higher precision would require an even larger simulation size! This is an example of an absolute precision stopping rule ( Section 5) and is unique since the limiting variance is known. For further discussion of this example, see Frey [8]. is a
is a 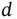 ‐dimensional target distribution, and interest is in estimating different features of
‐dimensional target distribution, and interest is in estimating different features of 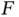 . In Monte Carlo simulation, we generate
. In Monte Carlo simulation, we generate 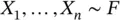 either via IID sampling or via a Markov chain that has
either via IID sampling or via a Markov chain that has  as its limiting distribution. For MCMC samples, we assume throughout that a Harris ergodic Markov chain is employed ensuring convergence of sample statistics to (finite) population quantities (see Roberts and Rosenthal [9], for definitions).
as its limiting distribution. For MCMC samples, we assume throughout that a Harris ergodic Markov chain is employed ensuring convergence of sample statistics to (finite) population quantities (see Roberts and Rosenthal [9], for definitions).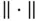 denote the Euclidean norm, and let
denote the Euclidean norm, and let 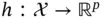 , so that interest is in estimating
, so that interest is in estimating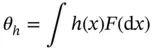
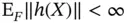 . If
. If 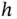 is identity, then the mean of the target is of interest. Alternatively,
is identity, then the mean of the target is of interest. Alternatively, 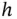 can be chosen so that moments or other quantities are of interest. A Monte Carlo estimator of
can be chosen so that moments or other quantities are of interest. A Monte Carlo estimator of  is
is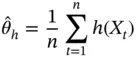
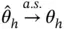 as
as 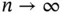 . The Monte Carlo average
. The Monte Carlo average 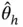 is naturally unbiased as long as the samples are either IID or the Markov chain is stationary.
is naturally unbiased as long as the samples are either IID or the Markov chain is stationary. is one‐dimensional (i.e.,
is one‐dimensional (i.e., 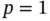 ). Extensions to
). Extensions to 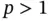 are straightforward but notationally involved [10]. For
are straightforward but notationally involved [10]. For 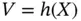 , interest may be in estimating a quantile of
, interest may be in estimating a quantile of 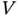 . Let
. Let 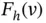 be the distribution function of
be the distribution function of 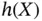 , assumed to be absolutely continuous with a continuous density
, assumed to be absolutely continuous with a continuous density 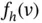 . The
. The 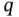 ‐quantile associated with
‐quantile associated with 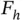 is
is![Роман Зыков - Роман с Data Science. Как монетизировать большие данные [litres]](/books/438007/roman-zykov-roman-s-data-science-kak-monetizirova-thumb.webp)










