7 Examples
7.1 Action Figure Collector Problem
Consider the general coupon collector problem [38] where the goal is to collect 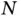 distinct objects (e.g., coupons, trading cards, and action figures). Specifically, independent draws of size
distinct objects (e.g., coupons, trading cards, and action figures). Specifically, independent draws of size 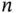 are made from
are made from 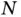 with replacement, and interest is in the number of draws necessary, say
with replacement, and interest is in the number of draws necessary, say 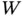 , to draw all
, to draw all 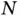 objects at least once. The classical case where
objects at least once. The classical case where 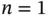 and all
and all 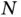 objects are equally likely yields a closed‐form solution (related to random sampling of digits). We consider a variation where
objects are equally likely yields a closed‐form solution (related to random sampling of digits). We consider a variation where 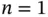 and
and 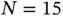 action figures appear in cereal boxes with probabilities in Table 1.
action figures appear in cereal boxes with probabilities in Table 1.
We estimate the expected number of boxes needed to collect all 15 action figures and the probability we needed to buy more than 100 and 200 total boxes. Denote these as 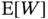 ,
, 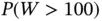 , and
, and 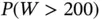 , respectively. Additionally, we implement an absolute precision sequential stopping rule to simulate until 95% confidence interval lengths for the three quantities of interest are below 1, 0.01, and 0.01, respectively. Specifically, we set
, respectively. Additionally, we implement an absolute precision sequential stopping rule to simulate until 95% confidence interval lengths for the three quantities of interest are below 1, 0.01, and 0.01, respectively. Specifically, we set 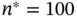 and simulate an additional 100 Monte Carlo sample between checking the stopping rule. The sequential stopping rule terminates at
and simulate an additional 100 Monte Carlo sample between checking the stopping rule. The sequential stopping rule terminates at 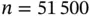 with estimates of
with estimates of 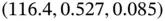 . We note that stopping is based on
. We note that stopping is based on  since its 95% confidence interval criteria is the most restrictive. The left panel of Figure 1provides a histogram of the Monte Carlo samples along with vertical bold lines corresponding to 100 and 200 boxes.
since its 95% confidence interval criteria is the most restrictive. The left panel of Figure 1provides a histogram of the Monte Carlo samples along with vertical bold lines corresponding to 100 and 200 boxes.
Table 1 Probabilities for each action figure
| Figures |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
| Probability |
0.2 |
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
0.05 |
0.05 |
0.05 |
0.05 |
0.02 |
0.02 |
0.02 |
0.02 |
0.02 |
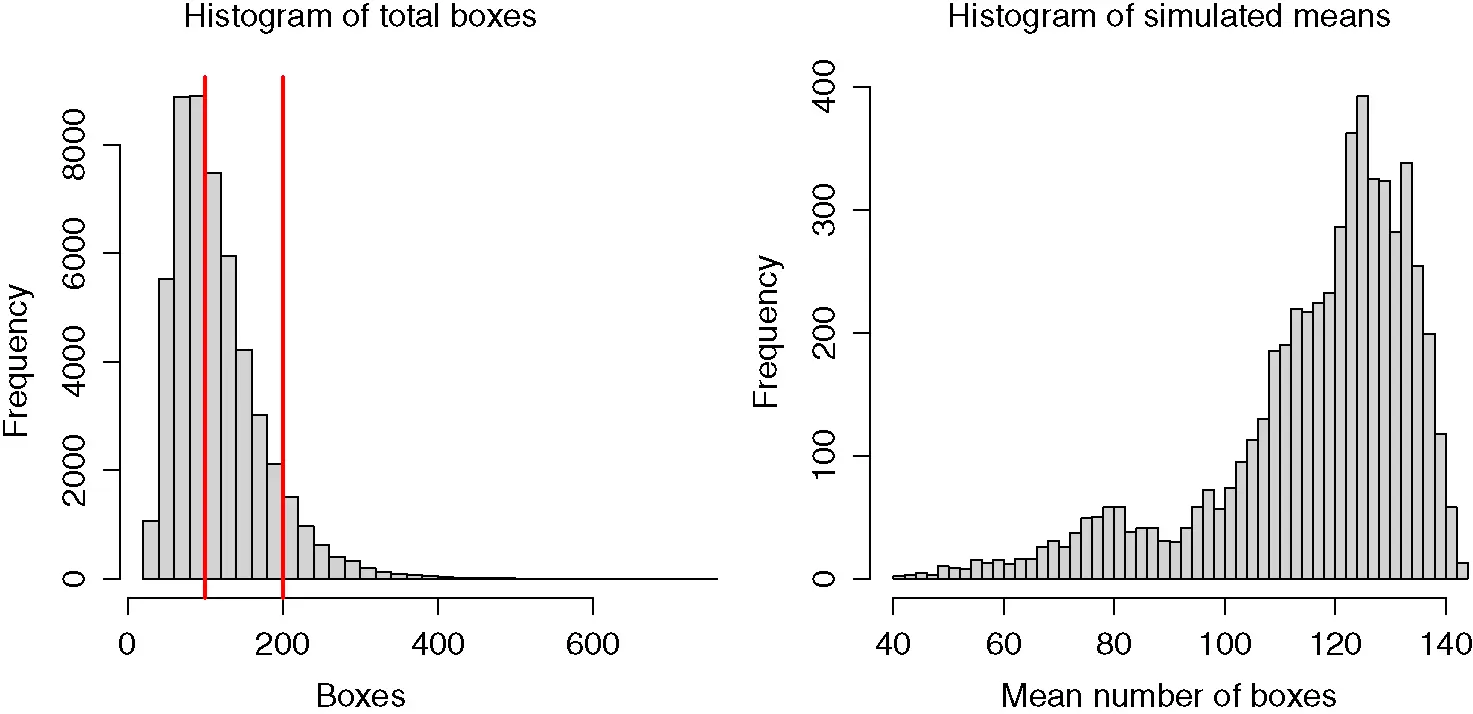
Figure 1 Histograms of simulated boxes and mean number of boxes for two Monte Carlo sampling strategies in the collector problem.
A more efficient Monte Carlo experiment is available if we only wish to estimate 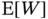 . Suppose that
. Suppose that 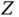 is the set of all permutations of the set
is the set of all permutations of the set 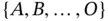 representing the order in which the action figures were collected. Then, for any
representing the order in which the action figures were collected. Then, for any 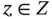 , we can calculate
, we can calculate 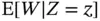 and notice
and notice
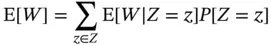
This calculation is unavailable since there are over 3 trillion partitions in 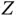 . However, we can simulate
. However, we can simulate  equally likely permutations from
equally likely permutations from 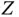 and estimate
and estimate 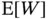 with
with
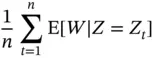
Using this sampler, we simulate until the 95% confidence interval length for 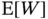 is below 1. Again, we set
is below 1. Again, we set 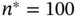 and simulate an additional 100 Monte Carlo sample between checking the stopping rule. Now the sequential stopping rule terminates at
and simulate an additional 100 Monte Carlo sample between checking the stopping rule. Now the sequential stopping rule terminates at 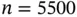 with an estimate of 116.1, which is approximately 10 times more efficient than the naive Monte Carlo sampling. The right panel of Figure 1provides a histogram of the Monte Carlo simulated means.
with an estimate of 116.1, which is approximately 10 times more efficient than the naive Monte Carlo sampling. The right panel of Figure 1provides a histogram of the Monte Carlo simulated means.
7.2 Estimating Risk for Empirical Bayes
Risk of empirical Bayes estimators is often not available in closed form, and Monte Carlo simulation is used to estimate it. Consider Example 3.3 from Robert and Casella [4] where for a fixed 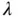 ,
,
Читать дальше

 distinct objects (e.g., coupons, trading cards, and action figures). Specifically, independent draws of size
distinct objects (e.g., coupons, trading cards, and action figures). Specifically, independent draws of size 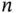 are made from
are made from 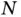 with replacement, and interest is in the number of draws necessary, say
with replacement, and interest is in the number of draws necessary, say 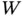 , to draw all
, to draw all 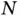 objects at least once. The classical case where
objects at least once. The classical case where 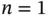 and all
and all 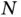 objects are equally likely yields a closed‐form solution (related to random sampling of digits). We consider a variation where
objects are equally likely yields a closed‐form solution (related to random sampling of digits). We consider a variation where 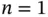 and
and 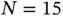 action figures appear in cereal boxes with probabilities in Table 1.
action figures appear in cereal boxes with probabilities in Table 1.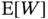 ,
, 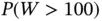 , and
, and 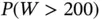 , respectively. Additionally, we implement an absolute precision sequential stopping rule to simulate until 95% confidence interval lengths for the three quantities of interest are below 1, 0.01, and 0.01, respectively. Specifically, we set
, respectively. Additionally, we implement an absolute precision sequential stopping rule to simulate until 95% confidence interval lengths for the three quantities of interest are below 1, 0.01, and 0.01, respectively. Specifically, we set 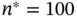 and simulate an additional 100 Monte Carlo sample between checking the stopping rule. The sequential stopping rule terminates at
and simulate an additional 100 Monte Carlo sample between checking the stopping rule. The sequential stopping rule terminates at 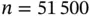 with estimates of
with estimates of 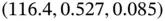 . We note that stopping is based on
. We note that stopping is based on 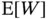 since its 95% confidence interval criteria is the most restrictive. The left panel of Figure 1provides a histogram of the Monte Carlo samples along with vertical bold lines corresponding to 100 and 200 boxes.
since its 95% confidence interval criteria is the most restrictive. The left panel of Figure 1provides a histogram of the Monte Carlo samples along with vertical bold lines corresponding to 100 and 200 boxes.
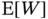 . Suppose that
. Suppose that 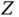 is the set of all permutations of the set
is the set of all permutations of the set 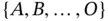 representing the order in which the action figures were collected. Then, for any
representing the order in which the action figures were collected. Then, for any 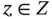 , we can calculate
, we can calculate 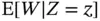 and notice
and notice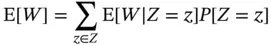
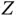 . However, we can simulate
. However, we can simulate  equally likely permutations from
equally likely permutations from 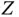 and estimate
and estimate 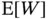 with
with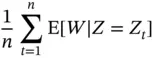
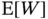 is below 1. Again, we set
is below 1. Again, we set 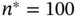 and simulate an additional 100 Monte Carlo sample between checking the stopping rule. Now the sequential stopping rule terminates at
and simulate an additional 100 Monte Carlo sample between checking the stopping rule. Now the sequential stopping rule terminates at 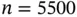 with an estimate of 116.1, which is approximately 10 times more efficient than the naive Monte Carlo sampling. The right panel of Figure 1provides a histogram of the Monte Carlo simulated means.
with an estimate of 116.1, which is approximately 10 times more efficient than the naive Monte Carlo sampling. The right panel of Figure 1provides a histogram of the Monte Carlo simulated means. ,
,![Роман Зыков - Роман с Data Science. Как монетизировать большие данные [litres]](/books/438007/roman-zykov-roman-s-data-science-kak-monetizirova-thumb.webp)










