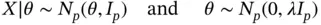
The posterior distribution of 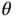 (given
(given 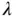 ) is
) is
If the true value of 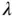 is unknown, it is often estimated from the marginal distribution of
is unknown, it is often estimated from the marginal distribution of 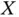 ,
, 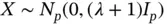 via maximum‐likelihood estimation as
via maximum‐likelihood estimation as
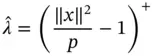
Robert and Casella [4] consider estimating 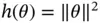 using the posterior mean
using the posterior mean 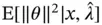 . Under a quadratic loss, the Bayes estimator is
. Under a quadratic loss, the Bayes estimator is
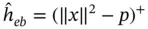
The risk for 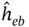
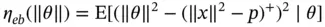
is difficult to obtain analytically (although not impossible, see Robert and Casella [4]). Instead, we can estimate the risk over a grid of 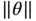 values using Monte Carlo. To do this, we fix
values using Monte Carlo. To do this, we fix  choices
choices  over a grid, and for each
over a grid, and for each 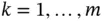 , generate
, generate 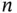 Monte Carlo samples from
Monte Carlo samples from 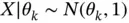 yielding estimates
yielding estimates
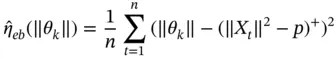
The resulting estimate of the risk is an 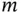 ‐dimensional vector of means, for which we can utilize the sampling distribution in Theorem 1to construct large‐sample confidence regions. An appropriate choice of a sequential stopping rule here is the relative‐magnitude sequential stopping rule, which stops simulation when the Monte Carlo variance is small relative to the average risk over all values of
‐dimensional vector of means, for which we can utilize the sampling distribution in Theorem 1to construct large‐sample confidence regions. An appropriate choice of a sequential stopping rule here is the relative‐magnitude sequential stopping rule, which stops simulation when the Monte Carlo variance is small relative to the average risk over all values of 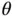 considered. It is important to note that the risk at a particular
considered. It is important to note that the risk at a particular  could be zero, but it is unlikely.
could be zero, but it is unlikely.
For illustration, we set 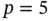 and simulate a data point from the true model with
and simulate a data point from the true model with 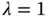 . To evaluate risk we choose a grid of
. To evaluate risk we choose a grid of 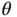 values with
values with 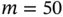 . In order to assess the appropriate Monte Carlo sample size
. In order to assess the appropriate Monte Carlo sample size 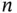 , we set
, we set 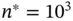 so that at least
so that at least 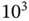 Monte Carlo samples are obtained. With
Monte Carlo samples are obtained. With 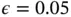 , and
, and  estimated using the sample covariance matrix, the sequential stopping rule terminates simulation at 21 100 steps. Figure 2demonstrates the estimated risk at
estimated using the sample covariance matrix, the sequential stopping rule terminates simulation at 21 100 steps. Figure 2demonstrates the estimated risk at 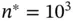 iterations and the estimated risk at termination. Pointwise Bonferroni corrected confidence intervals are presented as an indication of variability for each component 1 .
iterations and the estimated risk at termination. Pointwise Bonferroni corrected confidence intervals are presented as an indication of variability for each component 1 .
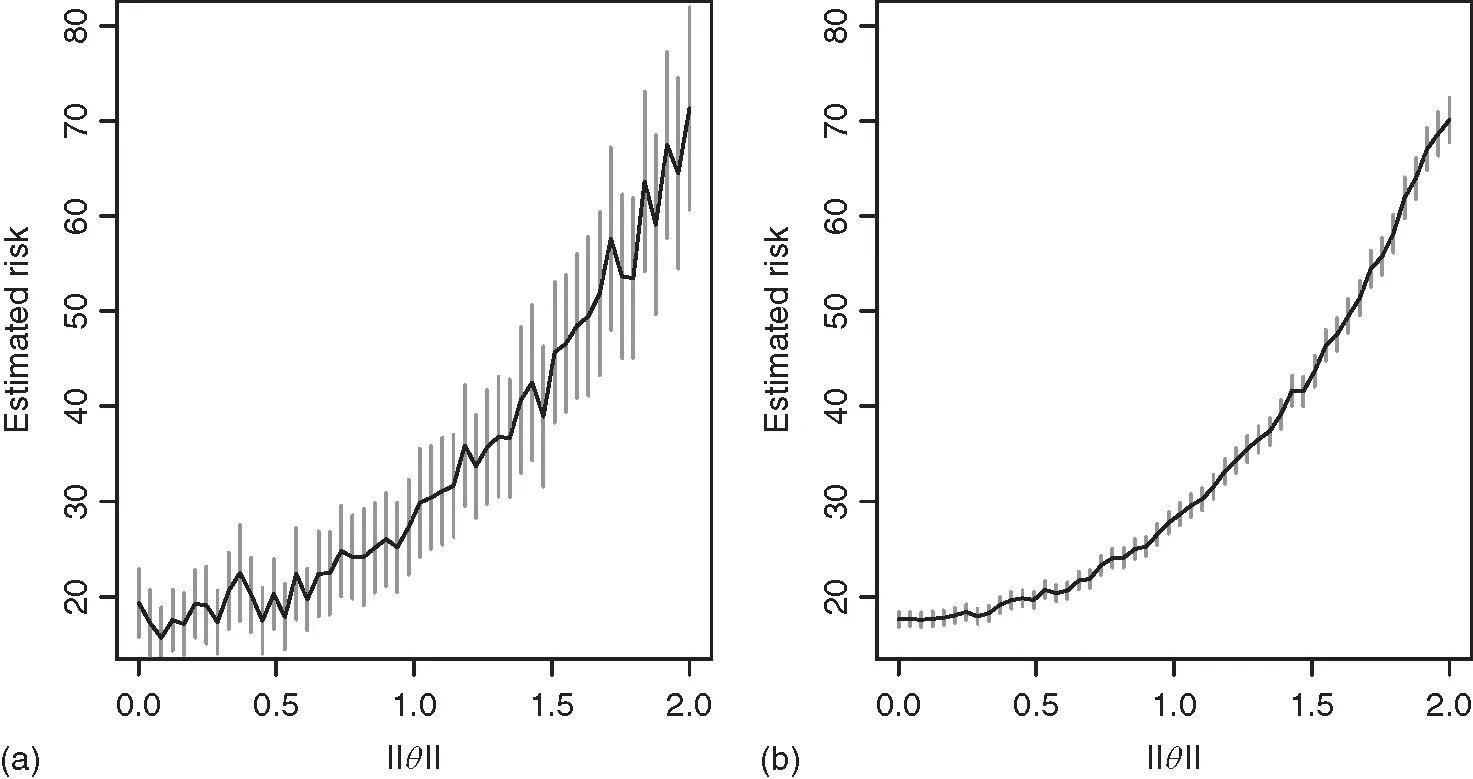
Figure 2 Estimated risk at 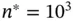 (a) and at
(a) and at 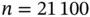 (b) with pointwise Bonferroni corrected confidence intervals.
(b) with pointwise Bonferroni corrected confidence intervals.
7.3 Bayesian Nonlinear Regression
Consider the biomedical oxygen demand (BOD) data collected by Marske [39] where BOD levels were measured periodically from cultured bottles of stream water. Bates and Watts [40] and Newton and Raftery [41] study a Bayesian nonlinear model with a fixed rate constant and an exponential decay as a function of time. The data is available in Bates and Watts [40], Section A4.1]. Let 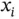 ,
, 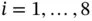 be the time points, and let
be the time points, and let 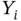 be the BOD at time
be the BOD at time 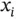 . Assume for
. Assume for  and
and 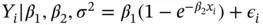 . Newton and Raftery [41] assume a default prior on
. Newton and Raftery [41] assume a default prior on 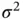 ,
, 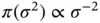 , and a transformation invariant design‐dependent prior for
, and a transformation invariant design‐dependent prior for 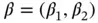 such that
such that 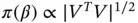 , where
, where 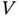 is an
is an 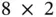 where the
where the 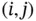 th element of
th element of 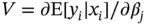 . The resulting posterior distribution of
. The resulting posterior distribution of 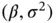 is intractable and up to normalization and can be written as
is intractable and up to normalization and can be written as
Читать дальше

 (given
(given 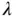 ) is
) is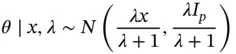
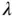 is unknown, it is often estimated from the marginal distribution of
is unknown, it is often estimated from the marginal distribution of 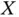 ,
,  via maximum‐likelihood estimation as
via maximum‐likelihood estimation as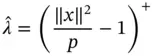
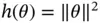 using the posterior mean
using the posterior mean 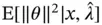 . Under a quadratic loss, the Bayes estimator is
. Under a quadratic loss, the Bayes estimator is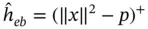
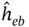
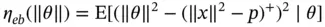
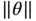 values using Monte Carlo. To do this, we fix
values using Monte Carlo. To do this, we fix 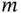 choices
choices 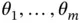 over a grid, and for each
over a grid, and for each 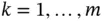 , generate
, generate 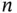 Monte Carlo samples from
Monte Carlo samples from 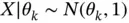 yielding estimates
yielding estimates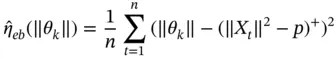
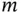 ‐dimensional vector of means, for which we can utilize the sampling distribution in Theorem 1to construct large‐sample confidence regions. An appropriate choice of a sequential stopping rule here is the relative‐magnitude sequential stopping rule, which stops simulation when the Monte Carlo variance is small relative to the average risk over all values of
‐dimensional vector of means, for which we can utilize the sampling distribution in Theorem 1to construct large‐sample confidence regions. An appropriate choice of a sequential stopping rule here is the relative‐magnitude sequential stopping rule, which stops simulation when the Monte Carlo variance is small relative to the average risk over all values of 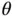 considered. It is important to note that the risk at a particular
considered. It is important to note that the risk at a particular  could be zero, but it is unlikely.
could be zero, but it is unlikely. and simulate a data point from the true model with
and simulate a data point from the true model with 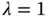 . To evaluate risk we choose a grid of
. To evaluate risk we choose a grid of 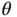 values with
values with 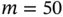 . In order to assess the appropriate Monte Carlo sample size
. In order to assess the appropriate Monte Carlo sample size 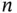 , we set
, we set 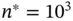 so that at least
so that at least 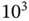 Monte Carlo samples are obtained. With
Monte Carlo samples are obtained. With 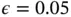 , and
, and 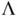 estimated using the sample covariance matrix, the sequential stopping rule terminates simulation at 21 100 steps. Figure 2demonstrates the estimated risk at
estimated using the sample covariance matrix, the sequential stopping rule terminates simulation at 21 100 steps. Figure 2demonstrates the estimated risk at 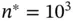 iterations and the estimated risk at termination. Pointwise Bonferroni corrected confidence intervals are presented as an indication of variability for each component 1 .
iterations and the estimated risk at termination. Pointwise Bonferroni corrected confidence intervals are presented as an indication of variability for each component 1 .
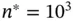 (a) and at
(a) and at 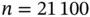 (b) with pointwise Bonferroni corrected confidence intervals.
(b) with pointwise Bonferroni corrected confidence intervals.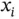 ,
, 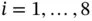 be the time points, and let
be the time points, and let 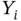 be the BOD at time
be the BOD at time 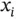 . Assume for
. Assume for  and
and 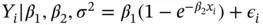 . Newton and Raftery [41] assume a default prior on
. Newton and Raftery [41] assume a default prior on 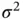 ,
, 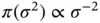 , and a transformation invariant design‐dependent prior for
, and a transformation invariant design‐dependent prior for 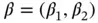 such that
such that  , where
, where 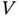 is an
is an 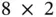 where the
where the 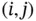 th element of
th element of 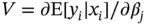 . The resulting posterior distribution of
. The resulting posterior distribution of 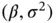 is intractable and up to normalization and can be written as
is intractable and up to normalization and can be written as![Роман Зыков - Роман с Data Science. Как монетизировать большие данные [litres]](/books/438007/roman-zykov-roman-s-data-science-kak-monetizirova-thumb.webp)










