3.2.4.3 The Consolidation Equation
In the standard treatment of consolidation equation (see, for instance, Lewis and Schrefler 1998), the acceleration terms are generally omitted a priori . However, as explained above, there is no disadvantage in writing the full dynamic formulation for solving such a problem. The procedure simply reduces the multiplier of the mass matrix Mto a negligible value without influencing in any way the numerical stability, provided, of course, that an implicit integration scheme is used.
3.2.4.4 Static Problems – Undrained and Fully Drained Behavior
Steady state (static) conditions will only be reached under the extremes of undrained or fully drained behavior. This can be deduced by rewriting the two, discrete, governing Equations (3.23)and (3.28)omitting terms involving time derivatives. The equations now become:
(3.55) 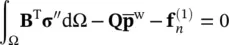
and
(3.56) 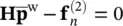
with the effective stresses given by (3.27)and are defined incrementally as
(3.57) 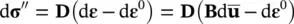
First, we observe that the equations are uncoupled and that the second of these, i.e. (3.56)can be solved independently of the first for the water pressures. Indeed, in this solution, the negative pressure zones and, hence, the partially saturated regions can be readily determined following the procedures outlined in the previous chapter.
With 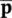 wdetermined as
wdetermined as
(3.58) 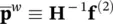
the first Equation (3.55)coupled with the appropriate constitutive law (3.57)can be solved once the history of the load applied has been specified.
The solution so obtained is, of course, the well‐known, drained , behavior.
The case of undrained behavior is somewhat more complex. We note that with k = 0, i.e. with totally impermeable behavior
(3.59) 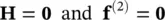
But on re‐examining Equation (3.28), we find that it becomes
(3.60) 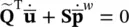
which, on integration, establishes a unique relationship between 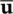 and
and 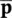 wwhich is not time‐dependent
wwhich is not time‐dependent
(3.61) 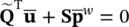
assuming that the initial condition of 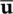 = 0and
= 0and 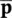 w= 0coincides.
w= 0coincides.
Equation (3.61)now has to be solved together with (3.55). If S= 0, i.e. no compressibility is admitted, then we have the problem already discussed in the previous Section 3.2.3in which only certain 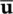 −
− 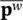 interpolations are permissible (as shown in Figure 3.2). However, if S≠ 0
interpolations are permissible (as shown in Figure 3.2). However, if S≠ 0 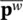 can be eliminated directly and the solution concerns only the variable
can be eliminated directly and the solution concerns only the variable 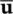 .
.
Solving (3.61)for 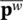 which can only be done provided that some fluid compressibility is available giving S≠ 0, then (3.55)and the constitutive law are sufficient to obtain the unique undrained condition.
which can only be done provided that some fluid compressibility is available giving S≠ 0, then (3.55)and the constitutive law are sufficient to obtain the unique undrained condition.
The existence of the two steady states is well known and what we have indicated here is a process by which various matrices given in the original computer program can be used to obtain either of the steady state solutions. However, this does require an alternative to the original computer program. Though, it is possible to obtain such steady states by the code, using the previous time‐stepping procedure. Two types of undrained conditions exist: (a) when k = 0 throughout; (b) k ≠ 0 but the complete boundary is impermeable. Both cases can be computed with no difficulties.
Provided that the boundary conditions are consistent with the existence of drained and undrained steady state conditions, the time‐stepping process will, in due course, converge with
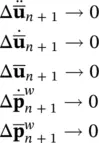
However, this process may be time‐consuming even if large time steps, Δ t are used. A simpler procedure is to use the GN00 scheme with
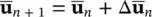
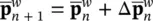
Equations (3.41)and (3.61)now become, for the undrained problem,
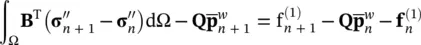
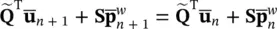
If the material behavior is linearly elastic, then the equation can be solved directly yielding the two unknowns 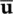 n+1and
n+1and 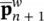 and if the material is nonlinear, an iteration scheme such as the Newton–Raphson, Quasi‐Newton, Tangential Matrix or the Initial Matrix method can be adopted. With a systematic change of the external loading, problems such as the load–displacement curve of a nonlinear soil and pore–fluid system can be traced.
and if the material is nonlinear, an iteration scheme such as the Newton–Raphson, Quasi‐Newton, Tangential Matrix or the Initial Matrix method can be adopted. With a systematic change of the external loading, problems such as the load–displacement curve of a nonlinear soil and pore–fluid system can be traced.
Читать дальше

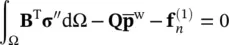
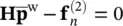
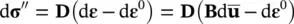
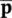 wdetermined as
wdetermined as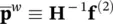
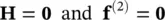
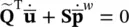
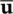 and
and 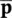 wwhich is not time‐dependent
wwhich is not time‐dependent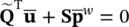
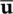 = 0and
= 0and 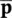 w= 0coincides.
w= 0coincides.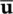 −
− 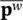 interpolations are permissible (as shown in Figure 3.2). However, if S≠ 0
interpolations are permissible (as shown in Figure 3.2). However, if S≠ 0 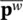 can be eliminated directly and the solution concerns only the variable
can be eliminated directly and the solution concerns only the variable 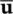 .
.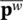 which can only be done provided that some fluid compressibility is available giving S≠ 0, then (3.55)and the constitutive law are sufficient to obtain the unique undrained condition.
which can only be done provided that some fluid compressibility is available giving S≠ 0, then (3.55)and the constitutive law are sufficient to obtain the unique undrained condition.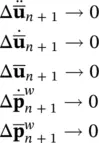
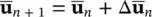
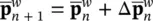
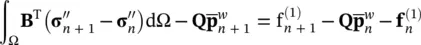
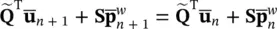
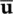 n+1and
n+1and 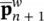 and if the material is nonlinear, an iteration scheme such as the Newton–Raphson, Quasi‐Newton, Tangential Matrix or the Initial Matrix method can be adopted. With a systematic change of the external loading, problems such as the load–displacement curve of a nonlinear soil and pore–fluid system can be traced.
and if the material is nonlinear, an iteration scheme such as the Newton–Raphson, Quasi‐Newton, Tangential Matrix or the Initial Matrix method can be adopted. With a systematic change of the external loading, problems such as the load–displacement curve of a nonlinear soil and pore–fluid system can be traced.










