Die Regel entspricht der Regel in Element (308) in Abschnitt 3.3.2 in DIN 18800-2 [K2]. Dort wird für die Ermittlung der vorhandenen Schubsteifigkeit der Bleche Bezug genommen auf DIN 18807 [K26], die nur zum Teil gleichwertig durch EN 1993-1-3 ersetzt wird.
Untersuchungen [K36] zeigen, dass der Einfluss der Verbindungsmittelsteifigkeit bei der Berechnung der Schubsteifigkeit S eines Trapezprofils eine zentrale Bedeutung hat. Die Verbindungsmittelsteifigkeit wird im ECCS-Dokument [K37], auf das in EN 1993-1-3 verwiesen wird, beachtet. Im zu EN 1993-1-3 gehörigen deutschen Nationalen Anhang DIN EN 1993-1-3/NA:2017 wird im NCI zu 10.3.1 derzeit zusätzlich auf DIN 18807-3 [K26] verwiesen. Die Werte in DIN 18807-3 ignorieren die Steifigkeit der Verbindungsmittel, womit die beiden Verweise also im Widerspruch zueinander stehen. Eine Überarbeitung des Verweises auf DIN 18807-3 ist in Arbeit.
(BB.3) 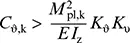
Dabei ist
| C ϑ,k |
die Verdrehsteifigkeit (je Längeneinheit Trägerlänge), die durch das stabilisierende Bauteil (z. B. die Dachkonstruktion) und die Verbindung mit dem Träger wirksam ist; |
| K υ |
= 0,35 für die elastische Berechnung; |
| K υ |
= 1,00 für die plastische Berechnung; |
| K ϑ |
der Faktor zur Berücksichtigung des Momentenverlaufs und der Art der Verdrehbarkeit des drehbehindert gestützten Trägers, siehe Tabelle BB.1; |
| M pl,k |
der charakteristische Wert der plastischen Momententragfähigkeit des Trägers. |
(2) B Die Verdrehsteifigkeit (je Längeneinheit Trägerlänge) durch das durchgehende Stabilisierungselement (z. B. die Dachkonstruktion) ist wie folgt zu berechnen:
(BB.4) 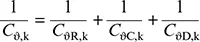
Dabei ist
| C ϑR,k |
die Verdrehsteifigkeit (je Längeneinheit) des stabilisierenden Bauteils unter der Annahme einer steifen Verbindung mit dem Träger; |
| C ϑC,k |
die Verdrehsteifigkeit (je Längeneinheit) der Verbindung zwischen dem Träger und dem stabilisierenden Bauteil; |
| C ϑD,k |
die Verdrehsteifigkeit (je Längeneinheit) infolge von Querschnittsverformungen des Trägers. |
Anmerkung: Weitere Informationen zur Bestimmung der Verdrehsteifigkeit, siehe EN 1993-1-3.
Zu BB.2.2(1)B
Bei der Unterscheidung für K ist mit den Begriffen elastische Berechnung plastische Berechnung tatsächlich die Ausnutzung des elastischen bzw. plastischen Querschnittswiderstands gemeint.
Zu BB 2.2(2)B und NCI
Es wird an dieser Stelle darauf hingewiesen, dass die Bezeichnungen für die Drehbettung und die Drehbettungsanteile unterschiedlich zu EN 1993-1-3 (Abschn. 10.1.5.2(1)) definiert sind. Im Folgenden sind die unterschiedlichen Bezeichnungen zusammenfassend dargestellt:
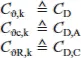
Formeln zur Ermittlung der Verdrehsteifigkeiten lassen sich unter anderem in [K18] und [K44] wiederfinden. Dabei ist darauf zu achten, dass für die Ermittlung der Verdrehsteifigkeit C ϑD,knach Formel (K.12) die Querschnittswerte in [cm] einzusetzen sind.
(K.12) 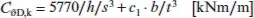
zu BB.2.2
Die Tabelle BB.1ist durch die folgende neue Tabelle BB.1 zu ersetzen:
Tabelle BB.1. Faktor K ϑzur Berücksichtigung des Momentenverlaufs und der Art der Lagerung in Abhängigkeit von der Biegedrillknicklinie nach Tabelle 6.5( Gl. (6.57))
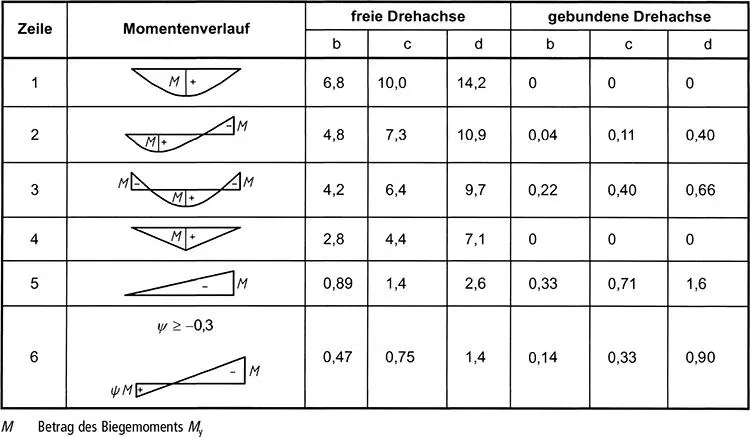
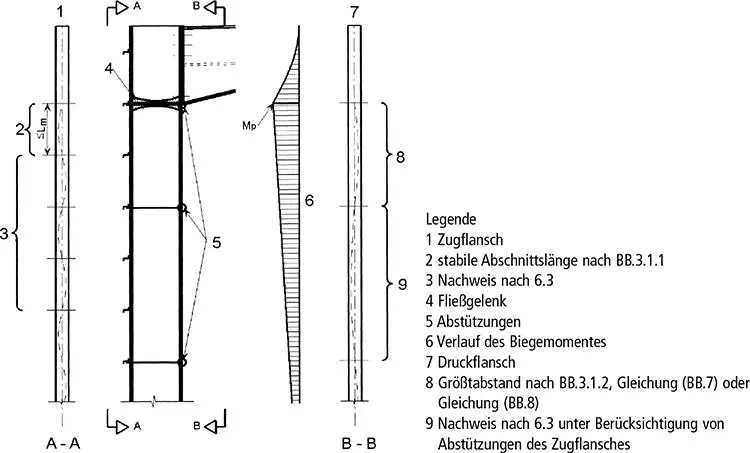
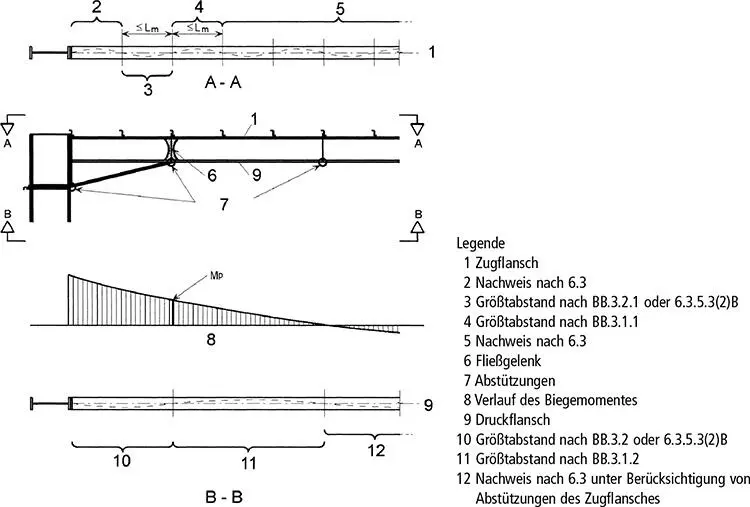
Bild BB.1. Angaben zu Nachweisen für Bauteile ohne Vouten
BB.3 Größtabstände bei Abstützmaßnahmen für Bauteile mit Fließgelenken gegen Knicken aus der Ebene
BB.3.1 Gleichförmige Bauteile aus Walzprofilen oder vergleichbaren geschweißten I-Profilen
BB.3.1.1 Größtabstände zwischen seitlichen Stützungen
(1)B Biegedrillknicken darf vernachlässigt werden, wenn die Abschnittslänge L , gerechnet von einem Fließgelenk bis zur nächsten seitlichen Stützung, nicht größer als L mist:
(BB.5) 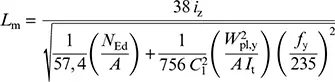
sofern das Bauteil am Fließgelenk entsprechend 6.3.5 gehalten ist und das andere Abschnittsende wie folgt gestützt wird, siehe Bild BB.1, Bild BB.2und Bild BB.3:
– entweder am Druckflansch, wenn ein Flansch über die gesamte Abschnittslänge im Druckbereich liegt;
– oder durch eine Verdrehbehinderung;
– oder durch seitliche Abstützung des Abschnittsende und eine zusätzliche Verdrehbehinderung, die den seitlichen Größtabstand Ls erfüllt.
Dabei ist
| N Ed |
die einwirkende Druckkraft, in N; |
| A |
die Querschnittsfläche, in mm 2; |
| W pl,y |
das plastische Widerstandsmoment; |
| I t |
das Torsionsflächenmoment 2. Grades; |
| f y |
die Streckgrenze, in N/mm 2; |
| C l |
ein von der Belastungssituation und den Lagerungsbedingungen abhängiger Faktor und kann als 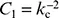 angenommen werden, wobei k cder Tabelle 6.6entnommen werden kann. angenommen werden, wobei k cder Tabelle 6.6entnommen werden kann. |
Anmerkung: Im Allgemeinen ist L sgrößer als L m.
Zu BB.3
Die Regelungen in diesem Abschnitt beruhen auf einer Tradition in England, Rahmentragwerke plastisch, also unter Ausnutzung der Schnittgrößenumlagerung aufgrund des nichtlinearen Werkstoffverhaltens, zu bemessen. Dies erfordert nach 6.3.5.1 eine seitliche Stützung an allen Fließgelenken mit Rotationsanforderungen entsprechend 6.3.5.2 und einen Stabilitätsnachweis für die Tragwerksabschnitte zwischen solchen Stützungen und anderen seitlichen Lagerungen entsprechend 6.3.5.3. Anhang BB.3 enthält detaillierte Regeln für den Stabilitätsnachweis in 6.3.5.3.
Man kann entweder den Nachweis führen, dass der Druckgurt in einem entsprechend engen Raster von L mgestützt ist, oder man weist eine dichte Stützung am Zuggurt und eine entsprechende Verdrehbehinderung des Druckgurtes im Abstand L kbzw. L snach. Die Regeln liegen in BB3.1 für parallelgurtige Profile und in BB3.2 für Voutenbereiche vor. Erläuterungen zur Anwendung des Verfahrens mit Beispielrechnungen sind in [K24] und [K25] zu finden.
Читать дальше

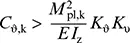
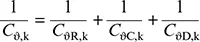
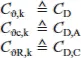
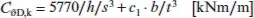


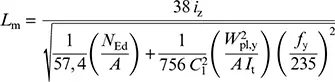
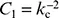 angenommen werden, wobei k cder Tabelle 6.6entnommen werden kann.
angenommen werden, wobei k cder Tabelle 6.6entnommen werden kann.











