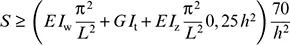Tabelle B.3.Äquivalente Momentenbeiwerte C mzu Tabelle B.1und B.2
(2) B Die Knicklänge L creines Gurtstabes mit I- oder H-Querschnitten darf zu 0,9 L für Biegeknicken in der Ebene und zu 1,0 L für Biegeknicken aus der Ebene angenommen werden, sofern nicht eine kleinere Knicklänge durch genauere Berechnung gerechtfertigt wird.
(3)B Fachwerkstäbe in Stegen können mit einer kleineren Knicklänge als der Systemlänge für Biegeknicken in der Ebene nachgewiesen werden, wenn die Verbindungen zu den Gurten und die Gurte dieses aufgrund ihrer Steifigkeit und Festigkeit zulassen (z. B. falls geschraubt Mindestanschluss mit 2 Schrauben).
(4)B Unter solchen Bedingungen und für übliche Fachwerke darf die Knicklänge L crfür Gitterstäbe für Biegeknicken in der Stegebene auf 0,9 L abgemindert werden, siehe BB.1.2.
BB.1.2 Gitterstäbe aus Winkelprofilen
(1)B Wenn die Gurte eine ausreichende Endeinspannung für Gitterstäbe aus Winkelprofilen darstellen und die Endverbindungen solcher Gitterstäbe ausreichend steif sind (falls geschraubt mindestens zwei Schrauben), dürfen die Exzentrizitäten vernachlässigt und die Endeinspannungen bei der Bemessung der Winkelprofile als druckbelastete Bauteile berücksichtigt werden. Der effektive Schlankheitsgrad 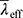 darf wie folgt ermittelt werden:
darf wie folgt ermittelt werden:
(BB.1) 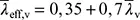
für Biegeknicken um die v-v -Achse;
(BB.1) 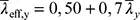
für Biegeknicken um die y-y -Achse;
(BB.1) 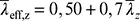
für Biegeknicken um die z-z -Achse;
wobei 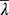 in 6.3.1.2 definiert ist.
in 6.3.1.2 definiert ist.
Zu Tabelle B.3
Die Werte C mgemäß den Formeln wurden für Knicklängen entsprechend den Stablängen entwickelt, vgl. Methode b) nach 5.2.2(7). Für das Ersatzstabverfahren gemäß 5.2.2(8) mit Knicklängen größer als die Stablängen bei verschieblichen Rahmen ist C mimmer zu 0,9 zu setzen, vgl. entsprechenden Hinweis in der Tabelle.
Die Koeffizienten α sund α hbestimmen sich nach dem Verhältnis der absoluten Momentenwerte für das Moment M han der Stützung und M sin Feldmitte. Falls der absolute Wert von M hgrößer ist als M s, dann gilt α s= M s/ M h(mit Vorzeichen) und die Formeln in den ersten 3 Zeilen gelten für die Bestimmung von C m. Im umgekehrten Fall, also der absolute Wert von M sist größer als M h, dann gilt α h= M h/ M s(mit Vorzeichen) und die Formeln in den letzten 3 Zeilen sind maßgebend für die Bestimmung von C m. Erläuterungen hierzu auch in [K52].
Der Begriff „in der Ebene gehalten“ für die Zuordnung der Momentenbeiwerte unten in der Tabelle B.3ist an dieser Stelle leider etwas unglücklich gewählt. Eigentlich sind hier die Halterungen in Richtung der entsprechenden Querschnittsachsen gemeint.
(2) B Wird lediglich eine einzige Schraube für die Endverbindungen der Gitterstäbe aus Winkelprofilen verwendet, ist in der Regel die Exzentrizität unter Verwendung von 6.2.9 zu berücksichtigen und die Knicklänge L crist als Systemlänge anzunehmen.
BB.1.3 Bauteile mit Hohlprofilen
(1) B Bei Gurtstäben mit Hohlquerschnitt darf die Knicklänge L crfür Biegeknicken in und aus der Ebene mit 0,9 L angenommen werden, wobei L die Systemlänge für die betrachtete Fachwerkebene ist. Die Systemlänge in der Fachwerkebene entspricht dem Abstand der Anschlüsse. Die Systemlänge rechtwinklig zur Fachwerkebene entspricht dem Abstand der seitlichen Abstützpunkte, sofern nicht ein kleinerer Wert durch genauere Berechnung rechtfertigt wird.
(2) B Die Knicklänge L creiner Fachwerkdiagonalen mit Hohlquerschnitt darf bei geschraubten Anschlüssen mit 1,0 L für Biegeknicken in und aus der Ebene angenommen werden.
(3) B Die Knicklänge L creines Verstrebungselements mit Hohlquerschnitt, die ohne Ausschnitte und Endkröpfungen angeschweißt ist, darf für Biegeknicken in und aus der Ebene mit 0,75 L angenommen werden. Geringere Knicklängen können basierend auf Prüfungen und Berechnungen verwendet werden. In diesem Fall darf die Knicklänge der Strebe nicht verringert werden.
Anmerkung: Weitere Informationen zu Knicklängen können im Nationalen Anhang angegeben sein.
zu BB.1.3(3)B Anmerkung
Für den Hochbau dürfen die Hinweise zu Knicklängen von Hohlprofilstäben in Fachwerkträgern in [1] verwendet werden.
Falls für die Streben ein Knicklängenfaktor von 0,75 oder niedriger verwendet wird, dann darf in derselben Einwirkungskombination die Knicklänge für die Gurtstäbe nicht reduziert werden.
BB.2 Kontinuierliche seitliche Abstützungen
BB.2.1 Kontinuierliche seitliche Stützung
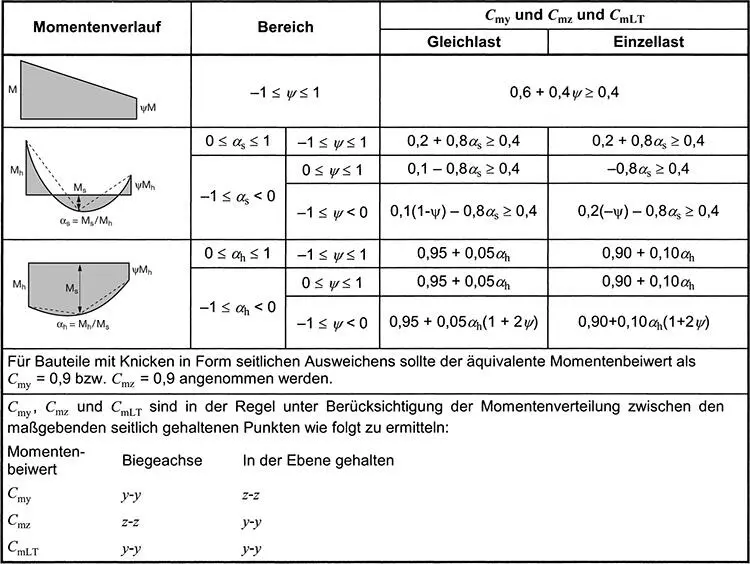
(1) B Wenn trapezförmige Bleche nach EN 1993-1-3 an jeder Rippe mit dem Träger verbunden werden und die Gleichung (BB.2)erfüllt wird, darf der Träger in der Ebene der Bleche als starr gelagert betrachtet werden.
(BB.2) 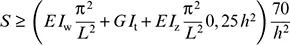
Dabei ist
| S |
die Schubsteifigkeit der Bleche (auf den untersuchten Träger entfallenen Anteil) im Hinblick auf die Verformungen des Trägers in der Blechebene; |
| I w |
das Wölbflächenmoment des Trägers; |
| I T |
das Torsionsflächenmoment des Trägers; |
| I z |
das Flächenträgheitsmoment des Trägerquerschnitts um die schwache Querschnittsachse; |
| L |
die Länge des Trägers; |
| h |
die Höhe des Trägers. |
Falls das Blech lediglich an jeder zweiten Rippe mit dem Träger verbunden ist, so sollte S durch 0,20 S ersetzt werden.
Anmerkung: Die Gleichung (BB.2)kann auch für den Nachweis der Seitenstabilität von Trägerflanschen bei anderen Scheibenkonstruktionen verwendet werden, wenn die Verbindungen geeignet sind.
BB.2.2 Kontinuierliche Drehbehinderung
(1) B Ein Träger darf als ausreichend gegen Verdrehung gestützt angesehen werden, wenn das folgende Kriterium erfüllt wird:
Zu NDP zu BB1.3(3)B Anmerkung
Wird durch Berücksichtigung einer gegenüber der Stablänge reduzierten Knicklänge für die Strebe eine Einspannung in die Gurtstäbe berücksichtigt, kann nicht gleichzeitig auch für die Gurtstäbe eine Einspannung in die Strebe angenommen werden.
Zu BB.2.1(1)B
Читать дальше


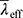 darf wie folgt ermittelt werden:
darf wie folgt ermittelt werden: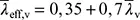
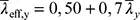
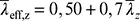
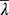 in 6.3.1.2 definiert ist.
in 6.3.1.2 definiert ist.