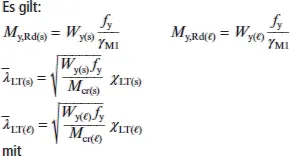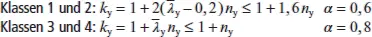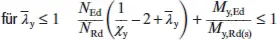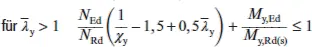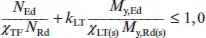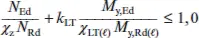Zwischenabstützungen gegen seitliches Ausweichen erfordern eine Abstützung beider Gurte des Profils oder eine Abstützung des einen Gurtes und zusätzliche Verdrehbehinderung des Querschnitts.
[K6], [K11], [K29] und [K32] enthalten Angaben auch zu vereinfachten Formulierungen für typische Einzelfälle wie Druck und einachsige Biegung und für den Fall verdrehsteifer Bauteile, wenn Biegedrillknicken keine Rolle spielt, vgl. auch Hinweise zu 6.3.2.1(2). Im Folgenden werden die vereinfachten Formulierungen aus [K32] dargestellt.
Für verdrehsteife Stäbe lautet der Biegeknicknachweis:
(K.3) 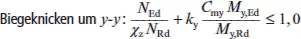
(K.4) 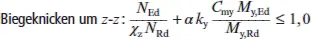
Für I-, H- und RHS-Querschnitte gilt vereinfacht:
(K.5) 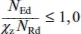
Die Beiwerte bestimmen sich zu:
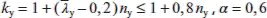
für Klassen 1 und 2
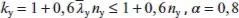
für Klassen 3 und 4
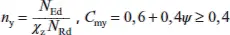
Für verdrehweiche Stäbe lautet der Biegedrillknicknachweis:
(K.6) 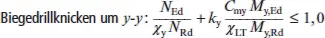
(K.7) 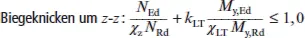
Der Beiwert k ybestimmt sich nach den obigen Gleichungen. Die anderen Beiwerte bestimmen sich zu:
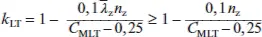
für Klassen 1 und 2 (für 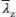 < 0, 4)
< 0, 4)
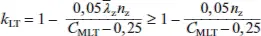
für Klassen 3 und 4
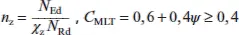
Für einfachsymmetrische I-, H-Querschnitte und rechteckige Hohlprofile sind in [K32] für den Fall Druck und einachsige Biegung um die starke Achse (Moment M yzusätzliche Regelungen angegeben, die eine Anwendung des Alternativverfahrens 2 auch für diesen Fall erlauben und im Folgenden wiedergegeben werden.
Dabei werden die Berechnungsformeln für den Standardfall eines zur z -Achse symmetrischen Querschnitts unter Druck und einachsiger Biegung M y,Edangegeben. Es sind in dem Fall positive und negative Werte für M y,Edzu unterscheiden. Laut Definition bewirkt ein positives Moment Druck am kleineren Gurt des Querschnitts. Die Biegebeanspruchbarkeiten M y,Rdund die Biegedrillknickschlankheiten 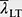 bzw. die zugehörigen Abminderungsfaktoren χ LTsind bei Querschnitten der Klassen 3 und 4 auf den jeweils maßgebenden kleineren oder größeren Gurt des Querschnitts zu beziehen, vgl. Bild K2.
bzw. die zugehörigen Abminderungsfaktoren χ LTsind bei Querschnitten der Klassen 3 und 4 auf den jeweils maßgebenden kleineren oder größeren Gurt des Querschnitts zu beziehen, vgl. Bild K2.
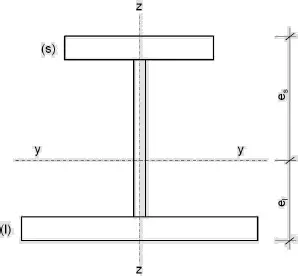
Bild K2. Querschnittsdefinitionen eines einfachsymmeterischen Querschnitts [K32]
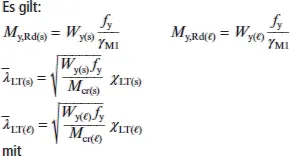
W y(s)Widerstandsmoment, bezogen auf den kleineren Gurt (s)
W y(ℓ)Widerstandsmoment, bezogen auf den größeren Gurt (ℓ)
M cr(s)Biegedrillknickmoment für positives Moment M y
M cr(ℓ)Biegedrillknickmoment für negatives Moment M y
Für verdrehsteife Stäbe gelten folgende Änderungen für die Beiwerte:
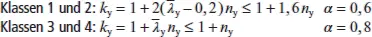
Dabei ist in die Bemessungsformeln für M y,Edder Absolutwert einzusetzen. Für Querschnitte der Klassen 3 und 4 ist M y,Rdfür den unter M y,Edgedrückten Rand zu bestimmen. Wird bei Querschnitten der Klassen 3 und 4 für negative Werte von M y,Eddie Zugspannung im kleineren Gurt maßgebend, sind folgende Gleichungen mit M y,Edals Absolutwert zu erfüllen:
(K.8) 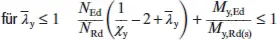
(K.9) 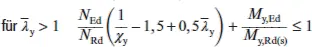
Für verdrehweiche Stäbe ist der oben aufgeführte Biegedrillknicknachweis um die y-y -Achse zu erfüllen. Dabei ist für M y,Edder Absolutwert einzusetzen. χ LTist für die Momentenrichtung von M y,Edzu bestimmen und bei Querschnitten der Klassen 3 und 4 ist M y,Rdfür den unter M y,Edgedrückten Rand zu bestimmen. Die Nachweise für Biegedrillknicken um die z-z -Achse lauten:
(K.10) 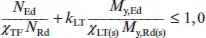
(K.11) 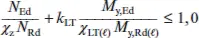
Dabei ist M y,Edvorzeichengerecht einzusetzen. Falls bei Querschnitten der Klassen 3 und 4 für negative Werte von M y,Eddie Zugspannung im kleineren Gurt maßgebend wird, sind die Gleichungen K.8 und K.9 zu erfüllen [K32]. Die Hintergründe dieser erweiterten Regeln auf einfachsymmetrische Querschnitte sind in [K35] beschrieben.
Spezielle Regelungen bei der Interaktion von Normalkraft und Biegung für kaltgeformte Querschnitte sind in DIN EN 1993-1-3 [K57] enthalten.
Planmäßige Torsion ist in den Gleichungen (6.61)und (6.62)nicht berücksichtigt. Der Anhang A von EN 1993-6 enthält hierzu ein Verfahren, das das Alternativverfahren 2 entsprechend ergänzt, vgl. auch [K44].
Tabelle 6.7.Werte für N Rk= ƒ y A i, M i,Rk= ƒ y W iund Δ M i,Ed
Читать дальше

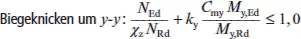
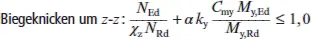
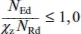
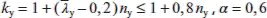
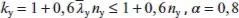
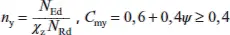
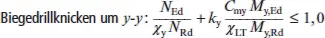
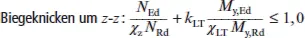
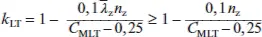
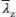 < 0, 4)
< 0, 4)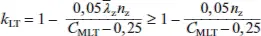
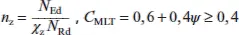
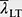 bzw. die zugehörigen Abminderungsfaktoren χ LTsind bei Querschnitten der Klassen 3 und 4 auf den jeweils maßgebenden kleineren oder größeren Gurt des Querschnitts zu beziehen, vgl. Bild K2.
bzw. die zugehörigen Abminderungsfaktoren χ LTsind bei Querschnitten der Klassen 3 und 4 auf den jeweils maßgebenden kleineren oder größeren Gurt des Querschnitts zu beziehen, vgl. Bild K2.