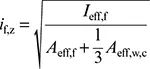
Dabei ist
| I eff,f |
das wirksame Flächenträgheitsmoment des druckbeanspruchten Flansches um die schwache Querschnittsachse; |
| A eff,f |
die wirksame Fläche des druckbeanspruchten Flansches |
| A eff,w,c |
die wirksame Fläche des druckbeanspruchten Teils des Stegblechs |
Anmerkung 2B: Der Nationale Anhang kann den Grenzschlankheitsgrad 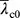 festlegen. Der Grenzwert von
festlegen. Der Grenzwert von 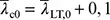 wird empfohlen, siehe 6.3.2.3.
wird empfohlen, siehe 6.3.2.3.
Zu 6.3.2.4
Der Nachweis des Biegedrillknickens wird hier als Nachweis des Knickens des Druckgurtes geführt. Dieses vereinfachte Modell berücksichtigt jedoch keine Abtriebseffekte infolge eines ungünstigen Lastangriffspunkts oberhalb des Schubmittelpunkts. Somit beschränkt sich die Anwendung des vereinfachten Druckgurtverfahrens auf Fälle ohne zusätzliche destabilisierende Momente. Die Vorgehensweise entspricht DIN 18800 Teil 2 [K2], Abschnitt 3.3.3 Element (310), indem zuerst nach Gleichung (6.59)ein Mindestabstand der seitlichen Stützung des Druckgurtes nachgewiesen werden kann und dann, wenn dieser Nachweis nicht erfolgreich ist, nach Gleichung (6.60)ein Knicknachweis geführt wird. Im Unterschied zu DIN 18800 Teil 2 wird hier der Gurtquerschnitt nicht um 1/5, sondern um 1/3 des Stegquerschnitts erhöht. Damit wird berücksichtigt, dass sich bei Spannungsgradienten im Steg, die über die gesamte Steghöhe Druckspannungen sind (z. B. bei Verbundträgern unter negativem Biegemoment) höhere Abtriebskräfte einstellen als bei typischen doppeltsymmetrischen Querschnitten unter reiner Biegung.
Diese Nachweisform ist nach EN 1993-1-1 entsprechend der Kennzeichnung B nur im Hochbau zulässig. Im Brückenbau wird aber in EN 1993-2 mit 6.3.4.2 „Vereinfachtes Verfahren“ der gleiche Nachweis zugelassen, mit dem Unterschied, dass in Gleichung (6.59)für 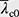 = 0,2 statt 0,5 und für k flin Gleichung (6.60)1,0 statt 1,1 zu wählen ist, was einer äußerst konservativen Regelung gleichkommt.
= 0,2 statt 0,5 und für k flin Gleichung (6.60)1,0 statt 1,1 zu wählen ist, was einer äußerst konservativen Regelung gleichkommt.
zu 6.3.2.4(1)B Anmerkung 2B
Es gilt die Empfehlung.
(2) B Wenn der Schlankheitsgrad 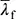 des druckbeanspruchten Flansches den in (1)B festgelegten Grenzwert überschreitet, darf der Bemessungswert der Biegedrillknickbeanspruchbarkeit wie folgt ermittelt werden:
des druckbeanspruchten Flansches den in (1)B festgelegten Grenzwert überschreitet, darf der Bemessungswert der Biegedrillknickbeanspruchbarkeit wie folgt ermittelt werden:
(6.60) 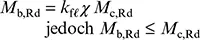
Dabei ist
| χ |
der mit 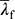 ermittelte Abminderungsfaktor des äquivalenten druckbeanspruchten Flansches; ermittelte Abminderungsfaktor des äquivalenten druckbeanspruchten Flansches; |
| k fℓ |
der Anpassungsfaktor, mit dem dem konservativen Nachweis mit äquivalenten druckbeanspruchten Flanschen Rechnung getragen wird. |
Anmerkung B: Der Nationale Anhang kann den Anpassungsfaktor k fℓfestlegen. Der Wert k fℓ= 1,10 wird empfohlen.
zu 6.3.2.4(2)B Anmerkung B
Es gilt die Empfehlung.
(3) B Für das Verfahren in (2)B sind in der Regel die folgenden Knicklinien zu verwenden:
Knickspannungslinie d für geschweißte Querschnitte, vorausgesetzt: 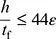 ;
;
Knickspannungslinie c für alle anderen Querschnitte.
Dabei ist
| h |
die Gesamthöhe des Querschnitts; |
| t f |
die Dicke des druckbeanspruchten Flansches. |
Anmerkung B: Zum Biegedrillknicken von seitlich gestützten Bauteilen im Hochbau, siehe auch Anhang BB.3.
6.3.3 Auf Biegung und Druck beanspruchte gleichförmige Bauteile
(1) Wenn keine Untersuchung nach Theorie II. Ordnung durchgeführt wird, bei der die Imperfektionen aus 5.3.2 angesetzt werden, sollte die Stabilität von gleichförmigen Bauteilen mit doppelt-symmetrischen Querschnitten, die nicht zu Querschnittsverformungen neigen, nach (2) bis (5) nachgewiesen werden. Dabei wird folgende Differenzierung vorgenommen:
– verdrehsteife Bauteile, wie z. B. Hohlquerschnitte oder gegen Verdrehung ausgesteifte Querschnitte;
– verdrehweiche Bauteile, wie z. B. offene Querschnitte, deren Verdrehung nicht behindert wird.
(2) Zusätzlich zu den Nachweisen nach (3) bis (5) sind an den Bauteilenden in der Regel Querschnittsnachweise nach 6.2 zu führen.
Zu 6.3.2.4(3)B
Für geschweißte Querschnitte ist dieses vereinfachte Verfahren nur zulässig, wenn die Voraussetzung h / t f≤ 44 ε eingehalten ist. Geschweißte Querschnitte, die diese Voraussetzung nicht erfüllen, dürfen mit diesem vereinfachten Modell nicht nachgewiesen werden. Mit dem Satz, dass Knickspannungslinie c für alle anderen Querschnitte zu verwenden ist, sind demnach die übrigen I-förmigen Walzquerschnitte gemeint. Hintergründe dazu lassen sich in [K58] wiederfinden.
Zu 6.3.3
Für Stäbe unter Druck und Biegung wird mit den Gleichungen (6.61)und (6.62)ein Doppelnachweis am aus dem System herausgeschnittenen Ersatzstab in allgemeiner Form gefordert, bei dem im Unterschied zu DIN 18800 Teil 2 [K2] Biegeknicken und Biegedrillknicken in einem gemeinsamen Nachweisformat behandelt werden und der Abminderungsfaktor für das Biegedrillknicken χ LTauch in der Nachweisgleichung (6.61)für Biegeknicken um die starke Achse zu berücksichtigen ist. Die Interaktionsfaktoren k yy, k yz, k zyund k zzkönnen wahlweise nach dem Alternativverfahren 1 in Anhang A oder dem Alternativverfahren 2 in Anhang B bestimmt werden. Die Hintergründe zu beiden Verfahren sind vom Technischen Komitee 8 der ECCS in der Dokumentation Nr. 119 [2] in der NCI Literaturliste erläutert worden. Während das Alternativverfahren 1 nur mithilfe eines Datenverarbeitungsprogramms sinnvoll zu verwenden ist, wurde das Alternativverfahren 2 im Anhang B aus deutsch/österreichischer Tradition heraus als auch noch für die Handrechnung geeignetes Verfahren entwickelt. Die Verfahren wurden am gabelgelagerten Einfeldträger für doppeltsymmetrische Querschnitte hergeleitet.
Die jeweiligen Stabendmomente müssen deshalb die Systemeinflüsse wie Effekte aus Theorie II. Ordnung und globale Imperfektionen – vorrangig Schiefstellungen – enthalten, vgl. auch Hinweise zu 5.2.2(7). Bei unterschiedlichen Halterungen in und aus der Ebene, das heißt unterschiedlichen Systemen, ist deshalb auch Methode b1) zu empfehlen, bei der alle Effekte nach Theorie II. Ordnung und aus Imperfektionen in der Ebene bei der Ermittlung der Schnittgrößen im Gesamtsystem komplett erfasst werden. Dann kann für das Alternativverfahren 2 auf die Anwendung von Gleichung (6.61)(Nachweis in der Ebene) verzichtet werden und mit Gleichung (6.62)lediglich der Nachweis aus der Ebene einschließlich Biegedrillknicken erfolgen. Andernfalls sind für beide Nachweisgleichungen getrennt die jeweiligen Stabendmomente nach Theorie II. Ordnung unter globalen Imperfektionen zu bestimmen.
Читать дальше

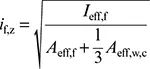
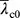 festlegen. Der Grenzwert von
festlegen. Der Grenzwert von 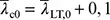 wird empfohlen, siehe 6.3.2.3.
wird empfohlen, siehe 6.3.2.3.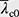 = 0,2 statt 0,5 und für k flin Gleichung (6.60)1,0 statt 1,1 zu wählen ist, was einer äußerst konservativen Regelung gleichkommt.
= 0,2 statt 0,5 und für k flin Gleichung (6.60)1,0 statt 1,1 zu wählen ist, was einer äußerst konservativen Regelung gleichkommt.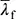 des druckbeanspruchten Flansches den in (1)B festgelegten Grenzwert überschreitet, darf der Bemessungswert der Biegedrillknickbeanspruchbarkeit wie folgt ermittelt werden:
des druckbeanspruchten Flansches den in (1)B festgelegten Grenzwert überschreitet, darf der Bemessungswert der Biegedrillknickbeanspruchbarkeit wie folgt ermittelt werden: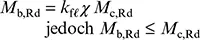
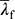 ermittelte Abminderungsfaktor des äquivalenten druckbeanspruchten Flansches;
ermittelte Abminderungsfaktor des äquivalenten druckbeanspruchten Flansches;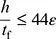 ;
;










