Rudolf Taschner - Die Zahl, die aus der Kälte kam - Wenn Mathematik zum Abenteuer wird

25 Wir denken uns drei Eingangsdrähte, mit p , q und r abgekürzt, parallel an sieben AND-Gatter angeschlossen.

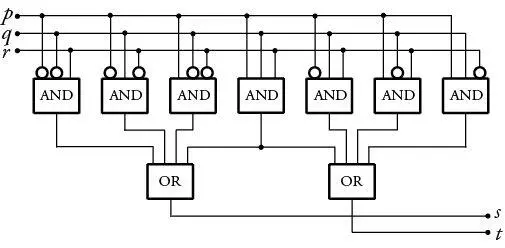
Vor den linken drei der sieben AND-Gatter werden jedoch abwechselnd vor je zwei der drei Eingänge in das jeweilige AND-Gatter NOT-Gatter gesetzt. Und vor den rechten drei der sieben AND-Gatter werden abwechselnd vor je einem der drei Eingänge in das jeweilige AND-Gatter NOT-Gatter gesetzt. Nur beim mittleren der sieben AND-Gatter laufen die Eingangsdrähte p , q , r direkt hinein. Der Ausgangsdraht des mittleren AND-Gatters verzweigt sich in zwei Drähte, die jeweils in ein OR-Gatter führen. In das linke dieser beiden OR-Gatter führen auch die Ausgangsdrähte der drei linken AND-Gatter, und in das rechte dieser beiden OR-Gatter führen auch die Ausgangsdrähte der drei rechten AND-Gatter. Den Ausgang des linken OR-Gatters symbolisieren wir mit s, und den Ausgang des rechten OR-Gatters symbolisieren wir mit t . Diese Schaltung nennt man einen Volladdierer . Denn welche Werte 0 oder 1 die Eingangsdrähte p , q , r auch besitzen, immer werden die Werte von s und t so sein, dass s + 2 t , im Sinne des Binärsystems von Leibniz: s + 10 t , mit der Summe p + q + r übereinstimmt: s symbolisiert die Einerstelle dieser Summe und t steht für den Übertrag auf die Zweierstelle, die ja im Binärsystem von Leibniz die 10-er-Stelle ist.

26 Die weiteren Ausführungen Hilberts bis zu seinen programmatischen Abschlusssätzen lauteten:

„In der Tat: Wir beherrschen nicht eher eine naturwissenschaftliche Theorie, als bis wir ihren mathematischen Kern herausgeschält und völlig enthüllt haben. Ohne Mathematik ist die heutige Astronomie und Physik unmöglich. Diese Wissenschaften lösen sich in ihren theoretischen Teilen geradezu in Mathematik auf. Diese wie die zahlreichen weiteren Anwendungen sind es, denen die Mathematik ihr Ansehen verdankt, soweit sie solches im weiteren Publikum genießt.

Trotzdem haben es alle Mathematiker abgelehnt, die Anwendungen als Wertmesser für die Mathematik gelten zu lassen.

Gauß spricht von dem zauberischen Reiz, den die Zahlentheorie zur Lieblingswissenschaft der ersten Mathematiker gemacht habe, ihres unerschöpflichen Reichtums nicht zu gedenken, woran sie alle anderen Teile der Mathematik so weit übertrifft.

Kronecker vergleicht die Zahlentheoretiker mit den Lotophagen, die, wenn sie einmal von dieser Kost etwas zu sich genommen haben, nie mehr davon lassen können.

Der große Mathematiker Poincaré wendet sich einmal in auffallender Schärfe gegen Tolstoi, der erklärt hatte, dass die Forderung ,die Wissenschaft der Wissenschaft wegen‘ töricht sei. Die Errungenschaften der Industrie, zum Beispiel, hätten nie das Licht der Welt erblickt, wenn die Praktiker allein existiert hätten und wenn diese Errungenschaften nicht von uninteressierten Toren gefördert worden wären.

Die Ehre des menschlichen Geistes, so sagte der berühmte Königsberger Mathematiker Jacobi, ist der einzige Zweck aller Wissenschaft.“

27 Ursprünglich hatte Schrödinger die Gleichung für ψ unter Berücksichtigung der Speziellen Relativitätstheorie Albert Einsteins aufgestellt. Weil ihm jedoch einige der möglichen Lösungen zu kurios schienen, formulierte er die Gleichung ohne Relativitätstheorie um. In dieser vereinfachten, unter dem Namen Schrödingergleichung bekannten Form, konnten die Quantentheoretiker sehr präzise die Eigenschaften der Atome und Moleküle beschreiben, denn in diesem Kontext spielt die Spezielle Relativitätstheorie praktisch keine Rolle. Schrödingers Kollege Paul Dirac nahm Schrödingers ursprüngliche Idee wieder auf und schrieb die Gleichung für ψ unter Einbeziehung der Speziellen Relativitätstheorie. Für jene Lösungen, die Schrödinger als zu kurios erachtete, fand Dirac physikalisch sinnvolle Deutungen. So ergab sich aus Diracs Gleichung, dass es zu jedem Elementarteilchen ein durch die entgegengesetzte Ladung gekennzeichnetes Antiteilchen geben müsse. Spätere Experimente bestätigten glanzvoll Diracs theoretische Vorhersage. Eine ψ-Gleichung unter Einbeziehung der Allgemeinen Relativitätstheorie Einsteins steht allerdings noch immer aus.

28 Einer launigen Legende zufolge soll ein Skeptiker Hilbert gegenüber geklagt haben, dass in seiner Geometrie nicht klar sei, worum es sich bei „Punkten“, „Geraden“ und „Ebenen“ eigentlich handle. In den Axiomen würden diese Begriffe wie sinnentleerte Wörter stehen und ihrer anschaulichen Bedeutung verlustig gehen. „Ganz recht“, soll Hilbert seinem Kollegen geantwortet haben, „auf das Wesen eines Begriffes kommt es in der formalen Mathematik nicht an.“ Man könne, so Hilbert, in seinem Axiomensystem statt „Punkte, Geraden und Ebenen“ jederzeit auch „Tische, Stühle und Bierseidel“ sagen.

29 Ganz so unerheblich ist die Frage nicht, ob endlich oder unendlich viele Nullen in der Dezimalentwicklung von π auftauchen. Man stelle sich die folgende Konstruktion einer Menge vor: Bei der ersten Null, die man in der Dezimalentwicklung von π findet, teilt man die Zahl 1 der Menge zu. Sobald man eine zweite Null in der Dezimalentwicklung von π findet, nimmt man zusätzlich 1/2 in die Menge auf. Sobald man eine dritte Null in der Dezimalentwicklung von π findet, nimmt man zusätzlich 1/3 in die Menge auf. Allgemein kommt auch die Bruchzahl 1/ n in die Menge, wenn man bereits n Nullen in der Dezimalentwicklung von π gefunden hat. Die Frage, ob endlich oder unendlich viele Nullen in der Dezimalentwicklung von π auftauchen, ist somit zur Frage gleichwertig, ob diese Menge aus endlich oder aus unendlich vielen Elementen besteht.

Diese Frage aber rührt an die Axiome des Rechnens mit unendlichen Dezimalzahlen. Denn die genannte Menge besteht aus lauter positiven Bruchzahlen und muss daher nach einem fundamentalen Axiom ein sogenanntes Infimum besitzen. Damit ist eine unendliche Dezimalzahl x gemeint, welche die folgenden beiden Eigenschaften besitzt: Einerseits ist jeder Bruch aus der Menge mindestens so groß wie x . Andererseits gibt es zu jedem y , das größer als x ist, einen Bruch aus der Menge, der kleiner als y ist.

Wie groß aber ist dieses Infimum x ?

Wenn nur endlich viele Nullen in der Dezimalentwicklung von π auftauchen, dann ist x = 1/ m jener positive Bruch, für den m die Anzahl der Nullen in der Dezimalentwicklung von π bezeichnet.

Wenn hingegen unendlich viele Nullen in der Dezimalentwicklung von π auftauchen, dann ist x = 0.

Und wenn es kein Ignorabimus geben darf, dann muss Hilbert entscheiden können, ob x positiv ist oder nicht. Somit führen selbst scheinbar unerhebliche Fragen zu diffizilen Problemen, die an den Grundfesten des Denkens rütteln.

30 Mit diesem Wort bringt Hermann Weyl in seiner Schrift „Über die neue Grundlagenkrise der Mathematik“ die Auffassung Hilberts am klarsten zum Ausdruck.

31 So schreibt es Anita Ehlers in ihrem schönen Buch „Liebes Hertz! Physiker und Mathematiker in Anekdoten“.

32 Henri Cartan und André Weil, zwei junge französische Mathematiker, die gemeinsam studiert hatten und zu Beginn der Dreißigerjahre an der Université Strasbourg wirkten, organisierten am 10. Dezember 1934 anlässlich ihrer regelmäßigen Teilnahmen an mathematischen Seminaren in Paris im Café Capoulade am Boulevard Saint-Michel ein Treffen mit anderen befreundeten jungen Kollegen. Die Gruppe beschloss, den veralteten Lehrbüchern der Universitäten ein modernes Werk entgegenzustellen. Es sollte sich dem Vortragsstil David Hilberts und Emmy Noethers angleichen, bei denen einige der Freunde Vorlesungen gehört hatten.