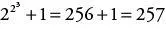a 1 = 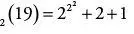
so:
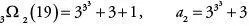 .
.
Das ist bereits eine ziemlich große Zahl, nämlich a 2 = 7 625 597 484 990. Das dritte Folgeglied a 3 ergibt sich aus
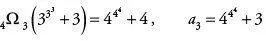 .
.
Dieses Folgeglied ist eine Zahl, die mit 13… beginnt und 155 Stellen besitzt. Das vierte Folgeglied a 4 ergibt sich aus
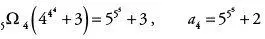 .
.
Dieses Folgeglied ist eine Zahl, die mit 18… beginnt und 2185 Stellen besitzt. Das fünfte Folgeglied a 5 ergibt sich aus
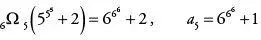 .
.
Dieses Folgeglied ist eine Zahl, die mit 26… beginnt und 36 306 Stellen besitzt. Schließlich ergibt sich das sechste Folgeglied a 6 aus der Rechnung
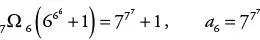 .
.
Dieses Folgeglied ist ein Zahlenmonster, das mit 38… beginnt und 659 974 Stellen besitzt. Die mit a = 19 beginnende Goodstein-Folge scheint ins Unermessliche zu wachsen.
Doch Goodstein behauptet, dass auch diese Folge irgendwann einmal bei Null enden wird. Es ist völlig unklar, auch Goodstein hat nicht die leiseste Ahnung, wie lange man darauf warten muss. Er stellt lediglich fest, dass es irgendwann geschieht. Sicher ist eine schier riesige Anzahl von Folgegliedern zu durchlaufen, jenseits aller Vorstellungskraft, jenseits auch aller Möglichkeiten, dies abzuschätzen, aber irgendwann, bei irgendeinem riesigen n = Θ(19), wird an + 1 = 0.
Goodstein behauptet sogar, dass die von ihm konstruierte Folge der Zahlen
a 1 , a 2 = 3Ω2( a 1) − 1, a 3 = 4Ω3( a 2) − 1, a 4 = 5Ω4( a 3) − 1,
a 5 = 6Ω5( a 4) − 1, …
stets bei Null enden muss, ganz egal, mit welcher Zahl a 1 man beginnt . Das ist eine verblüffende, eine geradezu ungeheuerliche Aussage. Nicht einmal für a 1 = 19 würde man es vermuten. Aber es stimmt, so teilt uns Goodstein mit, sogar für das Zahlenmonster a 1 = 3 ↑ ↑ ↑ 3. Und dies trotz der Tatsache, dass es uns nie gelingen wird 2(3 ↑ ↑ ↑ 3) anzugeben, weil schon das nächste Folgeglied a 2 = 3Ω2(3 ↑ ↑ ↑ 3) − 1 in unerreichbarer Ferne liegt.
Irgendwann, so versichert Goodstein, tritt der Fall ein, dass die verwendeten Basen, die ja mit jedem Folgeglied um 1 wachsen, die ins Gigantische explodierenden Folgeglieder einholen. Um dies jedoch begründen zu können, muss Goodstein das Unendliche, dem die berstenden Folgeglieder entgegenzustreben scheinen, als mathematisch sinnvollen Begriff fassen. Wir kommen darauf im letzten Kapitel zu sprechen. Ob sein mathematisches Modell des Unendlichen dem Wesen dieses Begriffs gerecht wird, ist allerdings eine offene Frage – und sie wird wahrscheinlich ewig offen bleiben.
Nimmt man das von Goodstein verwendete mathematische Modell des Unendlichen ernst, dann hat Goodstein tatsächlich recht. Es gibt nicht nur die Zahlen Θ(1), Θ(2), Θ(3) und Θ(4), es gibt auch Θ(19). Selbst Θ(3 ↑ ↑ ↑ 3) muss es geben – eine schwindelerregende Zahl.
11 Dies liegt daran, dass die Zahlen 10, 100, 1000, … bei der Division durch 3 immer den Rest 1 übrig lassen. Dividiert man eine Zahl wie zum Beispiel 4281 durch 3, bleibt bei der Division von 4000 durch 3 der Rest 4 × 1 = 4, bei der Division von 200 durch 3 der Rest 2 × 1 = 2, bei der Division von 80 durch 3 der Rest 8 × 1 = 8 und bei der Division von 1 durch 3 der Rest 1 × 1 = 1. Darum bleibt bei der Division von 4281 durch 3 der Rest 4 + 2 + 8 + 1 = 15, und diese Zahl ist durch 3 teilbar, lässt also als kleinstmöglichen Rest null.
12 Was Mersenne an diesen Beispielen zeigte, stimmt immer: Wenn man eine aus den Faktoren a und b zusammengesetzte Zahl a × b betrachtet, wobei sowohl a als auch b größer als 1 sind, dann ist
2 a × b − 1 = (2 a − 1) × (1 + 2 a + 22 a + … + 2( b – 1)× a )
eine zusammengesetzte Zahl.
13 Um der Wahrheit die Ehre zu geben: Fermat schrieb diese Zahlen als Potenztürme. Sie besitzen nämlich zugleich die Darstellungen
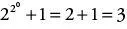 ,
, 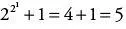 ,
, 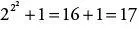 ,
, 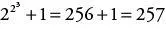
und so weiter.
14 Im Prinzip könnte man 4 294 967 297 der Reihe nach durch die Primzahlen aus einer genügend langen und vollständigen Primzahlentabelle dividieren und untersuchen, ob die Division ohne Rest aufgeht. Aber das ist nicht nur außerordentlich zeitaufwendig, es ist auch erbärmlich primitiv. Euler ging sicher anders vor. Vielleicht stellte er fest, dass 641 = 54 + 24 und zugleich 641 = 5 × 27 + 1 ist. Wegen der ersten Formel teilt 641 die Zahl (54 + 24) × 228 und wegen der zweiten Formel teilt 641 die Zahl 54 × (228 − 1), weil man deren zweiten Faktor in
228 − 1 = (27 + 1) × (221 − 214 + 27 − 1)
zerlegen kann. Wenn somit 641 die Zahlen (54 + 24) × 228 und 54 × (228 − 1) teilt, dann teilt sie auch deren Differenz, die
(54 + 24) × 228 − 54 × (228 − 1) = 24 × 228 + 1 = 232 + 1 = 4 294 967 297
beträgt.
15 Wir jedoch wollen verstehen: Warum funktioniert das eigenartige Verfahren des Chiffrierens und Dechiffrierens? Um diese Frage beantworten zu können, müssen wir weit ausholen und blicken auf Pierre de Fermat, jenen unerhört geistreichen Rechtsgelehrten aus der Zeit des Barock, der seine Freizeit am liebsten mit dem Studium der Zahlen zubrachte.
Man muss sich Fermat als vom Rechnen besessen vorstellen. Manisch suchte er den Zahlen Geheimnisse zu entlocken. So fiel ihm zum Beispiel auf, dass die fünften Potenzen aller Ziffern durchwegs mit eben dieser Ziffer an der Einerstelle enden: 05 = 0 endet mit 0, 15 = 1 endet mit 1, 25 = 32 endet mit 2, 35 = 243 endet mit 3, 45 = 1024 endet mit 4, 55 = 3125 endet mit 5, 65 = 7776 endet mit 6, 75 = 16 807 endet mit 7, 85 = 32 768 endet mit 8 und 95 = 59 049 endet mit 9. Und wie sieht das bei den dritten Potenzen aus? Da stimmt es nicht. Es ist zum Beispiel 23 = 8: diese Zahl endet nicht mit 2. Aber Fermat stellt fest, dass 23 − 2, also 8 − 2 = 6 durch die Hochzahl 3 teilbar ist. Das nämlich war es eigentlich, was er oben festgestellt hat: dass die fünfte Potenz jeder Ziffer minus eben dieser Ziffer durch fünf teilbar ist. Und er rechnet weiter: Es ist 33 − 3, also 27 − 3 = 24, und diese Zahl ist tatsächlich durch 3 teilbar. Genauso bestätigt er dass 43 − 4, also 64 − 4 = 60 durch 3 teilbar ist, dass 53 − 5, also 125 − 5 = 120 durch 3 teilbar ist, dass 63 − 6, also 216 − 6 = 210 durch 3 teilbar ist, dass 73 − 7, also 343 − 7 = 336 durch 3 teilbar ist, dass 83 − 8, also 512 − 8 = 504 durch 3 teilbar ist, ferner dass 93 − 9, also 729 − 9 = 720 durch 3 teilbar ist, dass sogar 103 − 10, also 1000 − 10 = 990 durch 3 teilbar ist und dass 113 − 11, also 1331 − 11 = 1320 durch 3 teilbar ist.
Читать дальше

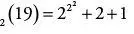
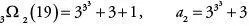 .
.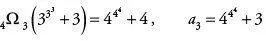 .
.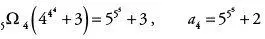 .
.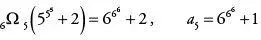 .
.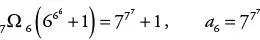 .
.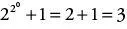 ,
, 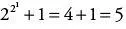 ,
, 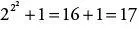 ,
,