42 = 8 × 5 + 2
8 = 1 × 5 + 3
1 = 0 × 5 + 1 .
Jetzt setzt man die einzelnen dieser Resultate ineinander ein:
42 = 8 × 5 + 2
= (1 × 5 + 3) × 5 + 2 = 1 × 52 + 3 × 5 + 2,
mit dem Ergebnis
42 = 1 × 52 + 3 × 5 + 2 = (1 3 2)5 .
Noch einfacher ist es, 42 zur Basis 7 darzustellen. Da gibt es nur zwei Divisionen
42 = 6 × 7 + 0
6 = 0 × 7 + 6 ,
woraus sich unmittelbar die Darstellung
42 = 6 × 7 + 0 = (6 0)7
ergibt. Genauso leicht ist die Darstellung von 42 zur Basis 10. Auch hier gibt es nur zwei Divisionen
42 = 4 × 10 + 2
4 = 0 × 10 + 4,
woraus die Darstellung
42 = 4 × 10 + 2 = (4 2)10
folgt. Die Darstellung einer Zahl zur Basis 10 ist uns seit Adam Ries wohlbekannt: Es ist die übliche Schreibweise von Zahlen im Dezimalsystem.
Im Folgenden sind aber die verschiedenen Basen wichtig. Denn nur so verstehen wir, was Goodstein das „Aufblähen“ einer Zahl nennt: Beim „Aufblähen der Zahl 42 von der Basis 5 zur Basis 6“ ersetzt man in der Darstellung
42 = 1 × 52 + 3 × 5 + 2
alle vorkommenden Zahlen 5 durch 5 + 1 = 6 und berechnet die dabei entstehende Zahl:
1 × 62 + 3 × 6 + 2 = 36 + 18 + 2 = 56.
Beim Aufblähen von der Basis 5 zur Basis 6 ist also aus 42 die größere Zahl 56 entstanden. Ebenso können wir 42 von der Basis 7 zur Basis 8 aufblähen: Ausgehend von 42 = 6 × 7 + 0 bildet man, weil 7 durch 7 + 1 = 8 ersetzt wird, 6 × 8 + 0 = 48. Hier ist aus 42 die Zahl 48 entstanden. Und beim Aufblähen der Zahl 42 von der Basis 10 zur Basis 11 ersetzt man 10 durch 10 + 1 = 11 und bildet 4 × 11 + 2. Es ergibt sich die aufgeblähte Zahl 46. Bevor wir die Zahl 42 von der Basis 2 zur Basis 3 aufblähen, müssen wir aber noch eine weitere Forderung berücksichtigen, die Goodstein beim Aufblähen erhob: 42 lautet zur Basis 2 bekanntlich
42 = 1 × 25 + 0 × 24 + 1 × 23 + 0 × 22 + 1 × 2 + 0.
Hier kommen Hochzahlen vor, die man ebenfalls zur Basis 2 darstellen kann, nämlich
5 = 1 × 22 + 0 × 2 + 1, 4 = 1 × 22 + 0 × 2 + 0,
3 = 1 × 2 + 1 und 2 = 1 × 2 + 0.
Diese Darstellungen der Hochzahlen fügt man in die obige Formel ein, so dass eine Darstellung von 42 entsteht, in der nirgendwo, auch nicht in den Hochzahlen, Zahlen vorkommen, die größer als 2 sind:
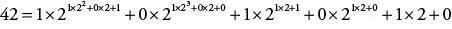 .
.
Der Einfachheit halber können wir in dieser Darstellung von 42, für die wir 2(42) schreiben, alle Summanden, bei denen der Faktor 0 auftaucht, weglassen. Also bleibt:
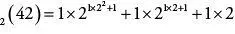 .
.
Jetzt bläht Goodstein die Zahl 42 von der Basis 2 zur Basis 3 auf, indem er überall, wo die Zahl 2 auftaucht, diese durch 2 + 1 = 3 ersetzt. Er bekommt somit
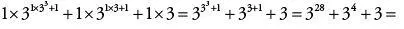 22 876 792 455 045.
22 876 792 455 045.
Ein solches Aufblähen hat es also in sich.
An dieser Stelle ist es von Nutzen, für das Aufblähen eine Bezeichnung einzuführen: Wir schreiben b ( a ), wenn wir die Zahl a zur Basis b darstellen, darin eingeschlossen auch alle vorkommenden Hochzahlen und wenn nötig auch die Hochzahlen dieser Hochzahlen, so dass nirgendwo in dieser Darstellung eine größere Zahl als b aufscheint. Ersetzt man nun alle in dieser Darstellung vorkommenden Zahlen b durch die um 1 größere Zahl b + 1, ist die Zahl a von der Basis b zur Basis b + 1 aufgebläht worden. Das Ergebnis, das Goodstein mit diesem Aufblähen erhält, nennen wir b + 1Ω b ( a ). Es sind 6Ω5(42) = 56, 8Ω7(42) = 48, 11Ω10(42) = 46 und 3Ω2(42) = 22 876 792 455 045.
Wie sich zeigt, wirkt sich das Aufblähen einer Zahl nur dann aus, wenn die Basis b höchstens so groß wie die Zahl a ist, die aufgebläht werden soll. So ist zum Beispiel 42 zur Basis 43 dargestellt nichts anderes als 42 selbst, und ein Ersetzen von 43 durch 44 ändert daran gar nichts. Also ist 44Ω43(42) = 42. Natürlich ist auch 100Ω99(42) = 42, allgemein gilt für jede Basis b , die größer als 42 ist, b + 1Ω b (42) = 42.
Wenn jedoch die Basis b viel kleiner als die Zahl a ist, explodiert b + 1Ω b ( a ) regelrecht.
Nun kommen wir zum Clou dessen, weshalb Goodstein diesen Begriff des Aufblähens einer Zahl erfand. Goodstein geht von irgendeiner Zahl a 1 aus. Zuerst stellt er a 1 zur Basis 2 dar, bildet also 2( a 1) und bläht die Zahl von der Basis 2 zur Basis 3 auf, das heißt, er berechnet 3Ω2( a 1). Von der so erhaltenen Zahl zieht er 1 ab, und nennt das Ergebnis a 2. Es ist also a 2 = 3Ω2( a 1) − 1. Diese Zahl a 2 stellt Goodstein zur Basis 3 dar und bläht die Zahl von der Basis 3 zur Basis 4 auf, er berechnet also 4Ω3( a 2). Die nächste Zahl a 3 seiner Folge bekommt er, wenn er von diesem Ergebnis 1 abzieht, das heißt: a 3 = 4Ω3( a 2) − 1. Jetzt stellt Goodstein a 3 zur Basis 4 dar, bläht sie von der Basis 4 zur Basis 5 auf, bildet also 5Ω4( a 3), und zieht, um die Zahl a 4 zu erhalten, davon wieder 1 ab: a 4 = 5Ω4( a 3) − 1. In dieser Weise fährt er immer weiter fort. Die Folgeglieder seiner Folge sind somit:
a 1 , a 2 = 3Ω2( a 1 ) − 1, a 3 = 4Ω3( a 2) − 1, a 4 = 5Ω4( a 3) − 1, a 5 = 6Ω5( a 4) − 1, …,
allgemein: an = n + 1Ω n ( an – 1) − 1.
Sehen wir uns zum Beispiel die Goodstein-Folge von a 1 = 3 an: Es ist 2(3) = 1 × 2 + 1, also 3Ω2(3) = 1 × 3 + 1 = 4, folglich a 2 = 3Ω2(3) − 1 = 4 − 1 = 3. Nun ist 3(3) = 1 × 3, also 4Ω3(3) = 1 × 4 = 4 und a 3 = 4Ω3(3) − 1 = 4 − 1 = 3. Als Nächstes lautet 4(3) = 3, hier ändert sich beim Aufblähen nichts: 5Ω4(3) = 3, und daher ist a 4 = 3 − 1 = 2. Es bleibt auch 6Ω5(2) = 2, also ist a 5 = 2 − 1 = 1, und es bleibt auch 7Ω6(1) = 1, also ist a 6 = 1 − 1 = 0. Von da an bleibt die Goodstein-Folge konstant null.
Bei der Goodstein-Folge von a 1 = 4 geht es bereits heftiger zu: Es ist 2(4) = 1 × 22, also 3Ω2(4) = 1 × 33 = 27, folglich a 2 = 3Ω2(3) − 1 = 27 − 1 = 26. Nun ist 3(26) = 2 × 32 + 2 × 3 + 2, also 4Ω3(26) = 2 × 42 + 2 × 4 + 2 = 42, folglich a 3 = 4Ω3(26) − 1 = 42 − 1 = 41. Als Nächstes lauten die Folgeglieder a 4 = 60, a 5 = 83, a 6 = 109, a 7 = 139. Scheinbar werden die Folgeglieder immer größer. Tatsächlich muss man ziemlich lange warten, bis diese Zunahme aufhört. Dann aber bleibt die Folge für lange Zeit konstant und nimmt schließlich – weil die Basis schon größer als das entsprechende Folgeglied geworden ist, Schritt für Schritt ab. Erst nach dem Folgeglied mit der Nummer 3 × 2402 653 211 (das ist eine Zahl mit mehr als 121 Millionen Stellen) wird endlich null erreicht.
Betrachtet man die Goodstein-Folge von einer Zahl a 1 und wird bei dieser Folge nach dem Folgeglied mit der Nummer n die Null erreicht, gilt also an = 1 und an +1 = 0, dann bezeichnen wir diese Nummer n mit n = Θ( a 1). Es sind zum Beispiel Θ(1) = 1, Θ(2) = 3, Θ(3) = 5 und Θ(4) = 3 × 2402 653 211.
Unglaublich rasant wächst die Goodstein-Folge zum Beispiel bei a 1 = 19. (Die Zahl 19 eignet sich gut zum Verständnis des Prozesses, weil wir hier wenigstens die nächsten paar Folgeglieder als Potenztürme aufschreiben können.) Das zweite Folgeglied a 2 errechnet sich wegen
Читать дальше

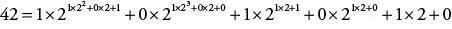 .
.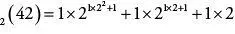 .
.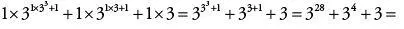 22 876 792 455 045.
22 876 792 455 045.










