Rudolf Taschner - Die Zahl, die aus der Kälte kam - Wenn Mathematik zum Abenteuer wird

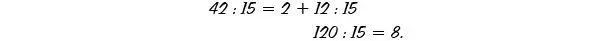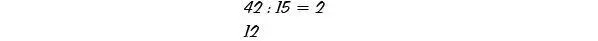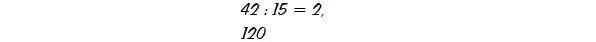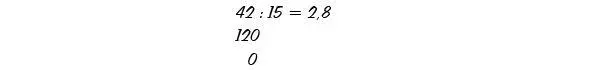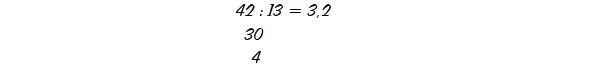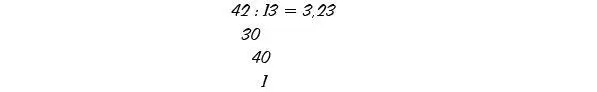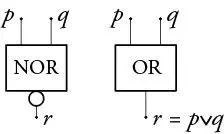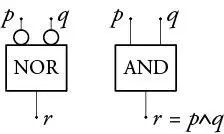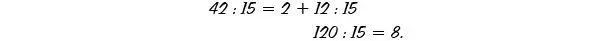
Das Ergebnis notiert er als Dezimalzahl 2,8. Grundschulkinder lernen die beiden Zeilen so zu schreiben: Zuerst die Division 42 durch 15 als

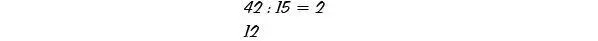
sie notieren also den Rest 12 säuberlich unter den Dividenden 42. Dann hängen sie an diesen Rest 0 an, malen nach dem bisher erhaltenen Quotienten 2 ein Komma

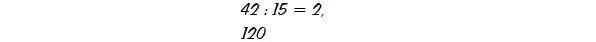
und dividieren im nächsten Schritt 120 durch 15 mit dem Ergebnis 8, nach dem Komma notiert, und dem Rest 0, unter 120 angeschrieben:

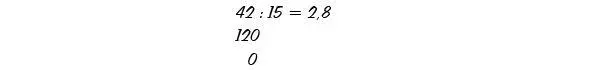
Bei der Division von 42 durch 13 sieht der Anfang ganz ähnlich aus:

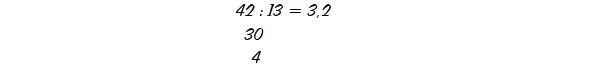
aber es ist noch immer ein Rest übrig geblieben. In diesem Fall schreibt uns Adam Ries vor, wieder Null an den Rest anzuhängen und weiterzumachen:

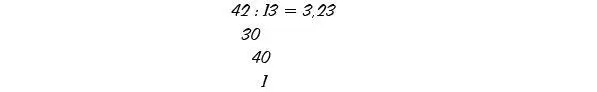
Wieder bleibt ein Rest. Also gilt es, mit der Prozedur immerzu fortzufahren:

Ein Ende des Verfahrens ist nicht absehbar. Allerdings taucht der erste Rest 3 wieder auf, also wiederholt sich die bisher angeschriebene Prozedur endlos. Als Ergebnis bekommt man eine „unendliche Dezimalzahl“

42 : 13 = 3,230769230769230769230769230769230769230769230769…,

bei der die Ziffernfolge 230769 die sogenannte Periode ist.

Es ist klar, dass es bei Divisionen immer zu periodischen unendlichen Dezimalzahlen kommt, wenn die Division nicht vorher abbricht. Denn irgendwann muss ein Rest, der schon vorher einmal erschienen ist, wieder auftauchen; es gibt ja nur endlich viele mögliche Reste, nämlich so viele, wie der Divisor, also die Zahl, durch die man dividiert, groß ist.

20 Für Kenner der Materie: Die Zahl 10 müsste eine sogenannte „Primitivwurzel“ des Divisors sein. Mit anderen Worten: Bezeichnet man den Divisor mit m und dividiert man der Reihe nach die Potenzen von 10 durch die Zahl m , dürfte erst bei der Division von 10 m – 1 durch die Zahl m der Rest 1 auftauchen. 10 ist zum Beispiel Primitivwurzel der Divisoren 7 oder 113, aber keine Primitivwurzel des Divisors 3 (schon 10 : 3 lässt den Rest 1) oder des Divisors 13 (es ist 13 × 76 923 = 999 999, also lässt die Division 106 : 13 den Rest 1).

21 Es könnte sogar glücken, dass eine viel kleinere Zahl als Divisor diese ellenlange scheinbare Zufallsfolge hervorbringt – im besten Fall eine Zahl, die selbst „nur“ um die zweihundert Stellen besitzt. Das ist natürlich erheblich kleiner als die Zahl, die aus 10200 Neunern besteht und daher 10200 Stellen besitzt. Allerdings müsste 10 eine Primitivwurzel dieses rund zweihundertstelligen Divisors sein.

22 Die Schlitze können mit einem darunter befindlichen langen Lineal abgedeckt werden: Schiebt man das Lineal nach oben, zeigen sich unterhalb wieder fünf Schlitze, und auch hier finden sich Ziffern eingetragen. Dabei ist es so, dass die Summe der Ziffern des jeweils oberen und unteren Schlitzes immer neun beträgt. Liest man zum Beispiel oben die Zahl 31415 und verdeckt man diese Zahl mit dem Lineal, erscheint unten die Zahl 68 584. Wir nennen sie die „Gegenzahl“ zur Zahl 31 415.

23 Auf den Walzen, welche die Ziffern tragen, die man in den Schlitzen sehen kann, hatte Pascal die zehn Ziffern zwischen Null und Neun jeweils in einer oberen Zeile und in einer unteren Zeile eingetragen: In der oberen Zeile in der Reihenfolge 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 so, dass sie mit der Drehung des entsprechenden Rades im Uhrzeigersinn der Reihe nach wachsen, und in der unteren Zeile in der gegenläufigen Reihenfolge 9, 8, 7, 6, 5, 4, 3, 2, 1, 0. Diese Ziffern der unteren Zeile sieht man nur dann, wenn man das bereits erwähnte Abdecklineal nach oben schiebt. Zeigte sich oben die Zahl 31 415, erblickt man unten die Zahl 68 584, die Gegenzahl von 31 415. Der Sinn dieser Vorrichtung besteht darin, nicht nur Additionen, sondern auch Subtraktionen mit der Pascaline durchzuführen. Eigentlich sollte die Subtraktion mit einem Drehen der Räder gegen den Uhrzeigersinn möglich sein, aber ein solches Drehen würde das Hebelwerk des Übertrags zerstören. Daher hemmt Pascal mit einer eigens eingerichteten Klinke das Drehen gegen den Uhrzeigersinn. Und er führt eine Subtraktion wie zum Beispiel 61 – 45 aufgrund des folgenden raffinierten Gedankens auf eine Addition zurück:

Die Gegenzahl von 61, nämlich 99 938, errechnet sich aus 99 999 − 61. Wenn man zu ihr 45 addiert, bekommt man

99 999 − 61 + 45 = 99 999 − (61 − 45).

Dies ist die Gegenzahl von jener Differenz 61 − 45, die wir suchen. Tatsächlich ergibt 99 938 + 45 die Zahl 99 983, und deren Gegenzahl ist 00016, wie es sein soll. Pascal geht daher bei der Berechnung von 61 − 45 folgendermaßen vor: Er stellt auf der Pascaline die Zahl 00061 auf den unteren Sehschlitzen ein. Auf den oberen Sehschlitzen würde deren Gegenzahl 99 938 aufscheinen, aber diese schaut er gar nicht an, sondern führt die scheinbare Addition von 45 bei geöffneten unteren Sehschlitzen durch und siehe da: Als Ergebnis taucht 00016 auf.

24 Die Schaltung, welche der logischen Aussage „nicht p “ entspricht, die man mit ¬ p abkürzt, heißt ein NOT-Gatter. Die Schaltung, welche der logischen Aussage „weder p noch q “ entspricht, die man mit p ↓ q abkürzt, heißt ein NOR-Gatter; die Buchstabenkombination NOR steht für „not or“.

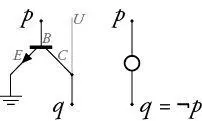
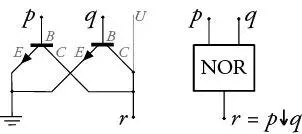
Ein NOR- und ein NOT-Gatter hintereinander geschaltet ergeben das OR-Gatter. Es entspricht der logischen Aussage „ p oder q oder beide“, und diese wird mit p ∨ q abgekürzt. Nur wenn p = 0 und q = 0 sind, ist auch p ∨ q = 0. In allen anderen Fällen ist p ∨ q = 1, denn in diesen ist ja mindestens eine der Aussagen p oder q wahr – genau dies entspricht dem nichtausschließenden „oder“.

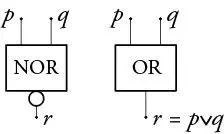
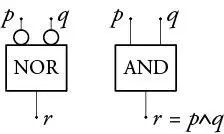
Zwei parallele NOT-Gatter und ein NOR-Gatter hintereinander geschaltet ergeben das AND-Gatter. Es entspricht der logischen Aussage „ p und q “ und diese wird mit p ∧ q abgekürzt. Nur wenn p = 1 und q = 1 sind, ist auch p ∧ q = 1. In allen anderen Fällen ist p ∧ q = 0, denn in diesen ist ja mindestens eine der Aussagen p oder q falsch, und genau dann ist „ p und q “ falsch.