(21.29)
где v r ' — компонента скорости заряда, параллельная r 12, т. е. направленная к точке (1). Сейчас я объясню, почему это так. Чтобы легче было следить за моими доводами, я сперва проведу расчет для «точечного» заряда в форме небольшого заряженного кубика, который движется к точке (1) со скоростью v(фиг. 21:5). Сторона куба будет а, это число пусть будет много меньше r 12[расстояния от центра заряда до точки (1)].
Чтобы оценить величину интеграла (21.28), мы вернемся к основному определению: запишем его в виде суммы
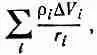
(21.30)
где r i — расстояние от точки (1) к i-му элементу объема DV i, а r i-— плотность заряда в DV iв момент t i =(t-r i /с). Поскольку все r i>> а, удобно будет выбрать все DV iв виде тонких прямоугольных ломтиков, перпендикулярных к r 12(фиг. 21.6).
Предположим, что мы начали с того, что взяли элементы объема DV iнекоторой толщины w, много меньшей а.
Отдельные элементы объема будут выглядеть так, как показано на фиг. 21.7, а. Их нарисовано гораздо больше, чем нужно, чтобы закрыть весь заряд. А сам заряд не показан, и по весьма существенной причине. Где его нужно нарисовать? Ведь для каждого элемента объема DV iнадо брать r в свой момент t~(t-r/с). Но раз заряд движется, то для каждого элемента объема DV i он окажется в другом месте!

Начнем, скажем, с элемента объема 1 на фиг. 21.7, а, выбранного так, чтобы в момент t l = (t-r 1 /с) «задняя» грань заряда пришлась на DV i(фиг, 21.7, б).
Фиг. 21.6, Элемент объема D V i , используемый для вычисления потенциалов.
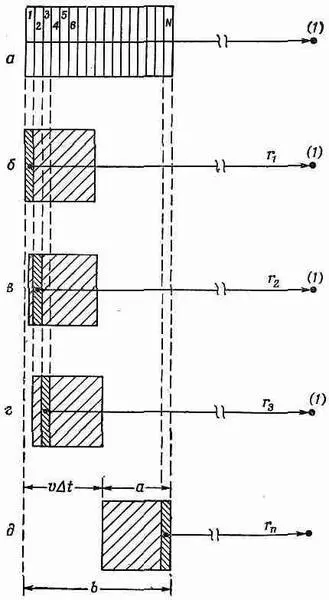
Фиг. 21.7. Интегрирование r(t-r'/c)dV для движущегося заряда.
Тогда, вычисляя r 2DV 2, нужно взять положение заряда в несколько более позднее время t 2 =(t- r 2 /c) и заряд к этому времени сместится в положение, показанное на фиг. 21.7, в. Так же будет с DV 3, DV 4и т. д. Вот теперь можно подсчитывать сумму.
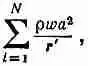
Толщина каждого DV i- равна w, а объем wa 2. Поэтому каждый элемент объема, накладывающийся на распределение заряда, содержит в себе заряд wa 2r, где r — плотность заряда внутри куба (мы считаем ее однородной). Когда расстояние от заряда до точки (1) велико, то можно все r iв знаменателях положить равными некоторому среднему значению, скажем, взятому с учетом запаздывания положению r ' центра куба. Сумма (21.30) превращается в
где DV N—тот последний элемент DV i, который еще накладывается на распределение зарядов (см. фиг. 21.7, д). Сумма тем самым равна
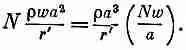
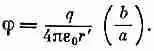
Но ra 3— просто общий заряд q, a Nw— длина b , показанная на фиг. 21.7, д. Получается
(21.31)
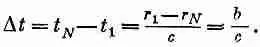
А чему же равно b? Это длина куба зарядов, увеличенная на расстояние, пройденное зарядом за время от t 1 =(t-r 1 /с) до t N =(t—r N /с). Это расстояние, пройденное зарядом за время
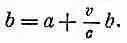
А поскольку скорость заряда равна v, то пройденное расстояние равно vDt = vb/c. Но длина b — само это расстояние плюс a:
Отсюда
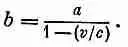
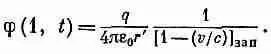
Здесь, конечно, под v подразумевается скорость в «запаздывающий» момент t' = (t-r'/с); это можно указать, записав [1— v/c] зап ; тогда уравнение (21.23) для потенциала принимает вид
Это согласуется с тем, что было предположено в (21.29). Появился поправочный множитель. Он появился потому, что в то время, как наш интеграл «проносится над зарядом», сам заряд движется. Когда заряд движется к точке (1), его вклад в интеграл увеличивается в b /а раз. Поэтому правильное значение интеграла равно q/r', умноженному на b /а, т.е. на 1/[1—v/c] з an.
Читать дальше

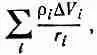


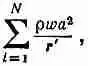
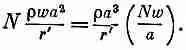
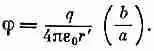
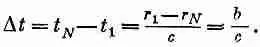
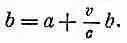
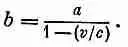
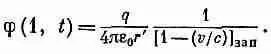



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
