5b. Электричество и магнетизм
§1. Диэлектрическая проницаемость
§2. Вектор поляризации Р
§З. Поляризационные заряды
§4. Уравнения электростатики для диэлектриков
§5. Поля и силы в присутствии диэлектриков
§ 1. Диэлектрическая проницаемость
Сейчас мы разберем еще одно характерное свойство материи, возникающее под влиянием электрического поля. В одной из предыдущих глав мы рассмотрели поведение проводников, в которых заряды под влиянием электрического поля свободно текут в такие участки, что поле внутри проводника обращается в нуль. Теперь мы будем говорить об изоляторах, т. е. таких материалах, которые не проводят электричество. Сначала можно было бы подумать, что в них вообще ничего не происходит. Но Фарадей с помощью простого электроскопа и конденсатора, состоящего из двух параллельных пластин, обнаружил, что это не так. Его опыт показал, что если между пластинами поместить изолятор, то емкость такого конденсатора увеличится. Когда изолятор целиком заполняет пространство между пластинами, емкость возрастает в x раз, причем x зависит только от свойств изолирующего материала. Изолирующие материалы называют также диэлектриками; тогда множитель x характеризует свойства диэлектрика и называется диэлектрической проницаемостью. Диэлектрическая проницаемость вакуума, конечно, равна единице.
Наша задача теперь состоит в том, чтобы объяснить, почему вообще возникает электрический эффект, раз изоляторы фактически являются изоляторами и не проводят электричества. Начнем с экспериментального факта, что емкость увеличивается, и попытаемся разобраться, что же там может происходить. Рассмотрим плоский конденсатор, на проводящих пластинах которого имеются заряды, скажем, на верхней пластине отрицательные, а на нижней — положительные.
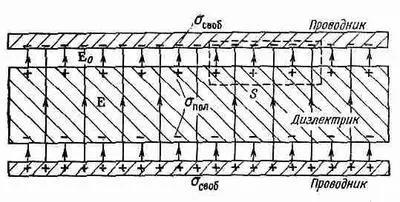
Фиг. 10.1. Плоский конденсатор с диэлектриком. Показаны линии паяя E.
Пусть расстояние между пластинами равно d, а площадь каждой пластины А. Как мы показали раньше, емкость равна
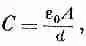
(10.1)
а заряд и потенциал конденсатора связаны соотношением
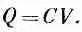
(10.2)
Далее, экспериментальный факт состоит в том, что если мы положим между пластинами кусок изолирующего материала, например стекла или плексигласа, то емкость возрастет. Это, разумеется, означает, что при том же заряде потенциал стал меньше. Но разность потенциалов есть интеграл от электрического поля, взятый поперек конденсатора; отсюда мы должны заключить, что электрическое поле внутри конденсатора стало меньше, хотя заряды пластин и не изменились.
Но как может это быть? Нам известна теорема Гаусса, которая утверждает, что полный поток электрического поля прямо связан с находящимся внутри объема электрическим зарядом. Рассмотрим входящую в теорему Гаусса поверхность S, изображенную пунктиром на фиг. 10.1. Поскольку электрическое поле в присутствии диэлектрика уменьшается, мы заключаем, что полный заряд внутри поверхности должен теперь быть меньше, чем до внесения изолятора. Остается сделать единственный вывод, что на поверхности диэлектрика должны находиться положительные заряды. Раз поле уменьшилось, но все же не обратилось в нуль, значит, этот положительный заряд меньше отрицательного заряда в проводнике. Итак, явление это можно объяснить, если мы поймем, почему на одной поверхности диэлектрика, помещенного в электрическое поле, индуцируется положительный заряд, а на другой — отрицательный.
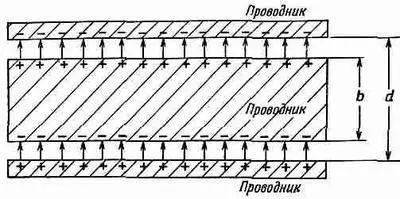
Фиг. 10.2. Если поместить пластинку проводника внутрь плоского конденсатора, наведенные заряды обратят поле в проводнике в нуль.
Все было бы понятно, если бы речь шла о проводнике. Пусть у нас был бы, например, конденсатор, расстояние между пластинами которого равно d, и мы вставили бы между этими пластинами незаряженный проводник толщиной b (фиг. 10.2). Электрическое поле индуцирует положительный заряд на верхней поверхности и отрицательный заряд на нижней поверхности, так что в результате поле внутри проводника погашается. Во всех остальных местах поле такое же, какое было без проводника, поэтому оно равно поверхностной плотности зарядов, деленной на e о; но расстояние, по которому мы должны интегрировать, чтобы получить напряжение (разность потенциалов), стало меньше.
Читать дальше


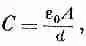
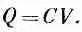





![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)

