Франческо Фьоретти - Тайната библиотека на Леонардо

Леонардо смяташе Чечилия Галерани за по-възвишена от всяка друга жена, включително и от херцогинята, от която дори беше по-елегантна в своята обикновеност и заради онзи неин строг и добър вкус, от който всеки художник би могъл да научи много.

Рисуваше набързо. След като привърши, каза, че ще се погрижи да нанесе скицата на ореховата дъска в работилницата си, без да се нуждае от модела. Щеше да поработи няколко дни и да се върне с готовия портрет. Сбогува се. Излезе от двореца с голямата си папка под мишница и реши да отиде при монаха математик в „Сан Франческо Гранде“.

Отново брат Амедео го придружи до килията на Лука Пачоли. Когато влезе, Леонардо бе посрещнат сърдечно от францисканеца, като че ли се познаваха от цяла вечност. Веднага щом пристъпи вътре, забеляза, че венецианската картина – портрета на монаха – вече я няма.

– В Урбино ли я изпратихте? – попита той, сочейки празното място на бюрото.

– Засега в Мантуа на сестрата на Беатриче, Изабела д’Есте, която от своя страна ще се погрижи да я изпрати в Урбино – отвърна брат Лука. – Джовани Гонзага е неин девер и шурей на Гуидобалдо да Монтефелтро. Надявам се от роднина на роднина портретът да стигне бързо до целта.

– На черната дъска имаше записан аритметичен сбор – отбеляза Леонардо.

Брат Лука взе хартия и перо, триъгълник и пергел. Начерта светкавично един равностранен триъгълник, вписан в окръжност, и други отсечки и добави редица числа в една колона:

– Ето – каза той, – това пишеше на дъската, подарявам ви го. Долу вляво е сборът, за който говорехте. Отсечката Aα ще допре окръжността, ако я довършим, предпочетох обаче да я оставя наполовина в картината, за да не правя задачата твърде лесна за придворните математици в Урбино, които ще видят портрета.

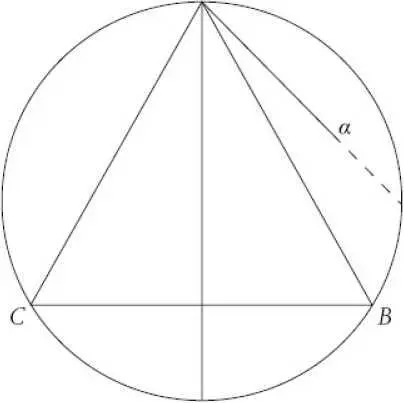
Пунктираната част от отсечката не присъства в творбата, но целият сегмент е страната на квадрата, вписан в кръга.

„Квадрат, вписан в кръга“? Леонардо разгледа внимателно чертежа. Диаметърът на окръжността е диагоналът на квадрата, вписан в нея. Страната на този квадрат е диагоналът на квадрата, построен върху радиуса. Ако си спомняше добре, според теоремата на Евклид, която математикът сочеше в книгата, квадратът, построен върху страна на равностранен триъгълник ABC , е равен на три пъти квадрата, построен върху радиуса.

– Следователно – каза той – отношението между лицата на двата квадрата, построения върху страната на триъгълника ABC и вписания в окръжността, е три към две, щом това е два пъти квадратът на ра​ диуса.

– Браво! – възкликна в отговор францисканецът. – Следователно отношението между радиусите на двете окръжности, които служат за построяване на двата квадрата, е корен от три върху корен от две, или корен от едно цяло и пет, което прави едно и двайсет и две до втората цифра след десетичната запетая, но е ирационално число, което е безкрайно.

Леонардо трудно следеше мисълта му. Като дете беше посещавал само един курс за използване на абак и не можеше да изчислява с корени. Да не говорим за алгебрата, която почти изобщо не познаваше. Същевременно започна веднага да изпитва силно възхищение към монаха. Точно в този миг реши, че ще станат приятели.

– Най-общо казано – заключи математикът, – ако разполагате само с триъгълник и пергел и искате да пос​ троите какъвто и да е икосаедър, единственото, което трябва да знаете, е едно число или една пропорция, едно отношение: корен от три върху корен от две, безкрайно число, едно цяло и двайсет и две и така нататък. Всички важни числа, които представляват синтаксиса на Космоса, са безкрайни. Като Бог. Математиката ни свързва именно с вечността и безкрайността на божествената субстанция.

– А какво е значението на числата в долната част?

– Енигмата на числата не бива да бъде разкрита на никого – отвърна монахът. – Простете, но тя следва да остане в тайна. Само херцогът на Урбино трябва да знае решението. Самият той поиска от мен преди известно време – и аз веднага удовлетворих желанието му – почти неразгадаем шифър от числа за защита на свръхтайна информация и обекти. Предполагам, че ми има доверие, при положение че все още съм жив. Държа тайнствената цифра да фигурира в картината под формата на загадка. Предизвикателство за придворните математици, които си придават важност. За да се стигне до решението, трябва да се потърси и прочете теоремата на Евклид, която посочвам с лявата си ръка, след това да се проследи фигурата, която рисувам на дъската, и най-после да се вникне в математическата игра на този сбор. Никой от тях никога няма да го пос​ тигне. Нито дори Паоло да Миделбьорг, епископ на Фосомброне, придворен математик и астролог, не ще бъде в състояние да реши загадката, а щом даже той не успее, това ще ми гарантира, че Гуидобалдо да Урбино ще спи спокойно, сигурен в недостъпността на своя шифър.