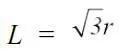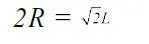Франческо Фьоретти - Тайната библиотека на Леонардо

Така и не се разбра почти нищо за престъплението в „Сан Франческо Гранде“. Единствено самоличността на убития благодарение на неговия портрет. Дори не се казвал Еджидио, а Пиерлеони да Римини – благородник, предан на Сиджизмондо Малатеста и на неговата съпруга Изота, която трябвало да си тръгне от адриатическия град след смъртта на владетеля, чийто незаконороден син, който бил наполовина от Фано, си присвоил властта. През последните години беше живял във Флоренция и бе признат не за посланик на Римини, а за един от Флорентинската република. Що се отнася до останалото, стана точно така, както Леонардо беше предвидил. Един престъпник от Боргачо, вече заподозрян за няколко злодеяния, на третото изпъване на ставите на раменете под натиска на въжето си призна половин дузина престъпления, сред тях и случилото се в „Сан Франческо Гранде“. Обесиха го още същия ден. Правосъдието беше въздадено. Нови ридания, нови сираци, нови утрешни крадци, които да бъдат обесени в бъдеще при подобни неотложни случаи. На съвестта на истинския убиец сега тежаха двама мъртъвци, а онези, дето изпитваха жажда за справедливост, успяха да я утолят.

Да начертаем квадрат със страна AX, с пергела да намерим центъра на основата му и от нея, допирайки двата срещуположни края, да начертаем полуокръжност, като, за да има още една допирна точка, удължаваме страната AX до B. Върху тази по-дълга отсечка построяваме правоъгълник, чиято височина е същата удължена отсечка BX:

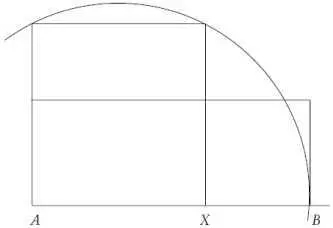
Отношението между AB и AX е равно на отношението между AX и BX: ако AX е златното сечение на AB, то BX, или AB минус AX, е златно сечение на AX, AX минус BX е златното сечение на BX и така до безкрай.

Освен това на тази фигура правоъгълникът, построен върху AB, и квадратът, построен върху AX, са еднакви, защото ако AB се отнася към AX, както AX към BX, то квадратът на средната пропорционална отсечка, AX 2, или квадратът на фигурата е равен на AB х BX, или основа за височина на правоъгълника. Също да кажем, че резултатът от тази пропорция е число, което е част от божествената безкрайност: ако AB всъщност е равно на 10, то AX ще бъде корен квадратен от 125 минус 5, или 6,18034, и така нататък в редицата на десетичните числа, която няма край, число, което наричаме „ирационално “, а BX, или 10 минус AX, е друго безкрайно число.

Това нарича учителят Лука „божествена пропорция “ и тя има невероятни свойства в петоъгълника и десетоъгълника. Аз самият я открих във Витрувианския човек, нарисуван в кръга и в квадрата, и мога да кажа, че този Витрувиански човек може да се впише в петоъгълника с ръце и крака, разперени в максимална степен. Но тъй като съм изследвал различни хора във „фабриката “ и тъй като наистина съм откривал, че са различни по размери и по отношенията между отделните части, в края на краищата стигнах до идеята, че тази пропорция, макар и съвсем невероятна със своето значение, няма реално участие в човешкото начало.

Ще се опитам да пресъздам разсъжденията, които брат Лука крие в картината за херцога на Урбино.

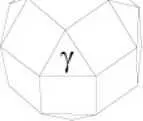
Ще начертая окръжност и квадрат, вписан в нея. След това ще построя равностранен триъгълник върху квадрата, ще намеря центъра и с пергела ще опиша около триъгълника още една окръжност. Трябва да се виждат диагоналите на двете окръжности:

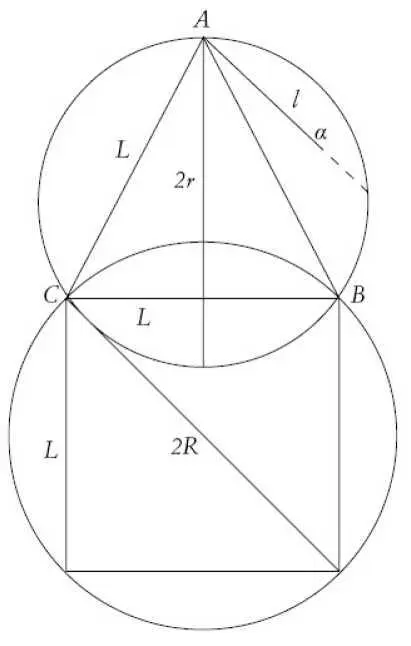
Нека R да бъде радиусът на голямата окръжност, r – радиусът на по-малката, L – страната на равностранния триъгълник и на квадрата, построен върху него, l – страната на квадрата, вписан в окръжността около триъгълника, и нека сегментът, който брат Лука не е довършил в картината, да е α. От теоремата на Евклид, посочена от математика, отнасяща се до отношението между страната L на равностранния триъгълник и радиуса r на окръжността, в която той е вписан (L 2= 3r 2), получавам накратко необходимата ми информация. От величините в теоремата на Евклид образувам

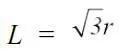
Сега диагоналът на квадрата, или диаметърът на окръжността 2R, е равен на корен от два пъти страната L

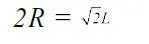
L: 2R = , Където, ако заместя страната L с нейния еквивалент