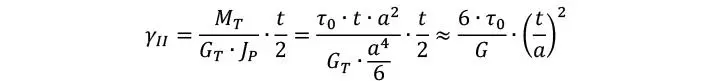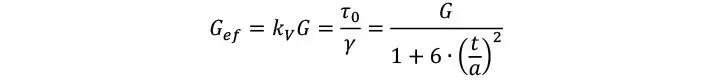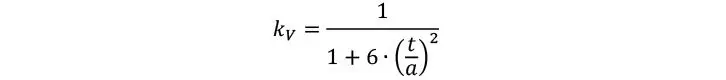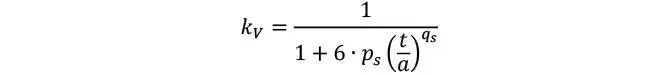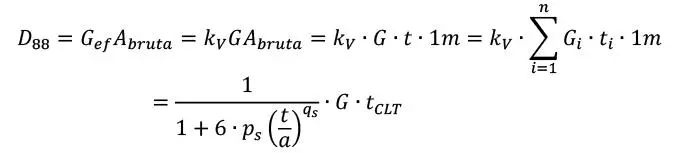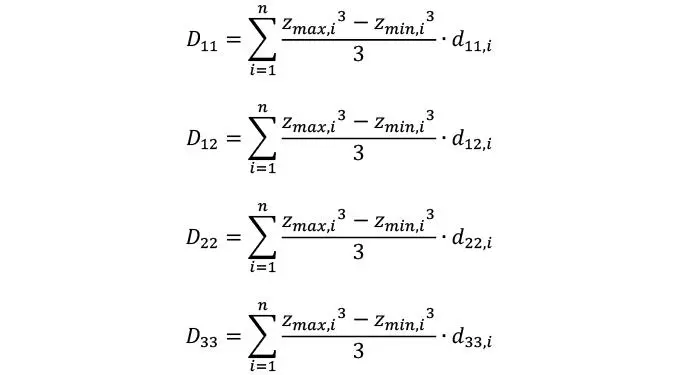Imaginemos ahora en nuestra discretización del tablero en RVSE, que las tablas no están encoladas en los bordes. Bajo estas circunstancias, no existe transmisión de corte longitudinal en los bordes en cada una de las láminas, por lo que al solicitar a corte una de las 2 láminas que conforman un RVSE, la transmisión del corte únicamente sería efectiva por la torsión con la otra lámina, lo que es referido como mecanismo de transmisión II. Así, la deformación torsional que se produciría se ilustra en la Figura 1.3.7.2 derecha.
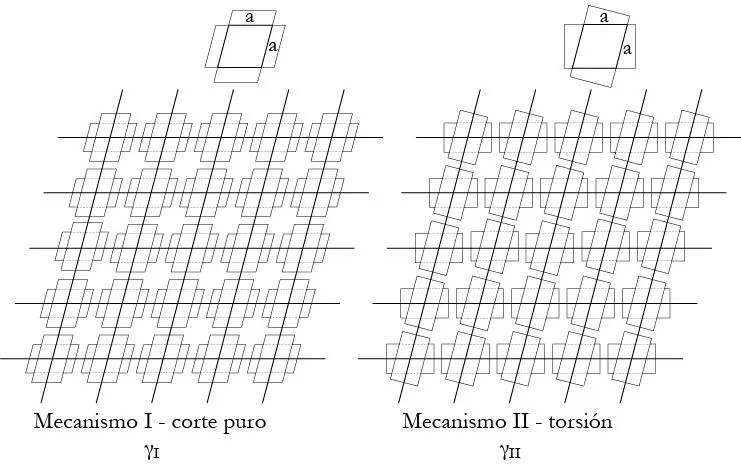
FIGURA 1.3.7.2 Descomposición del comportamiento a corte del RVSE como mecanismos de corte puro, mecanismo I, y torsión pura, mecanismo II (basado en Schickhofer et al. 2009).
En la realidad, lo que ocurre no es ni el mecanismo I ni el mecanismo II. Lo que ocurre realmente, es que los tablones de una lámina son únicamente efectivos al par de corte transversal a los tablones, pero no al par longitudinal de corte, y el equilibrio interno únicamente es proporcionado por los momentos torsores entre láminas. El mérito de la teoría de Schickhofer fue en gran medida, descubrir que el mecanismo real de corte del CLT puede verse como la suma aditiva de los mecanismos I y II, ya que bajo esas circunstancias los tableros únicamente transmiten el corte según par transversal, ver Figura 1.3.7.3.
FIGURA 1.3.7.3 Deducción de la transmisión real de corte del CLT consistente en transmisión de par transversal entre láminas como composición aditiva de los mecanismos I y II (basado en Schickhofer et al. 2009).
Así, el mecanismo I puede verse como la dupla de fuerzas transversales a los tablones en cada una de las láminas, mientras que el mecanismo II representa el momento torsor que se produce en cada una de las láminas como consecuencia de la dupla de cortantes transversales, ver Figura 1.3.7.4. Si es que se producen los 2 mecanismos de forma conjunta al solicitar una placa al corte cabe preguntarse cuál es el mecanismo más limitante. De nuevo, esta pregunta puede contestarse con la relación t/a tal como se muestra en la Figura 1.3.7.5, pues la solicitación a la torsión de la madera está íntimamente ligada a esta relación. Básicamente, para relaciones t/a por debajo de 0,15 la solicitación de torsión es siempre inferior al valor de resistencia de la madera a la torsión en la zona próxima al adhesivo entre láminas (aprox. 2,5 MPa en tensiones últimas), así es que la rotura siempre sucede por el mecanismo I, de corte. Sin embargo, para relaciones mayores (tablones más esbeltos), la solicitación puede rebasar la resistencia a la torsión (representada como una línea horizontal en la Figura 1.3.7.5) así es que en esas situaciones la rotura se producirá por torsión según el mecanismo II.
FIGURA 1.3.7.4 Esfuerzos internos producidos en los mecanismos I y II en cada una de las tablas del RSVE (basado en Schickhofer et al. 2009).
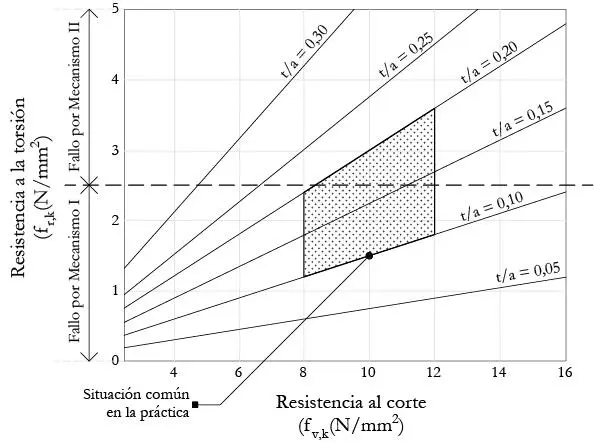
FIGURA 1.3.7.5 Típica determinación del mecanismo de fallo al corte de acuerdo a la relación t/a de las láminas de CLT. El fallo a torsión según el mecanismo II, únicamente se produce para valores superiores a la horizontal de resistencia torsional (basado en Schickhofer et al. 2009).
La deducción analítica del factor de corrección ahora es bien sencilla. La deformación por corte es, lógicamente, la composición de deformaciones en serie. La deformación angular debida al mecanismo I se puede estimar muy precisamente como la relación entre la tensión cortante compuesta (que es la mitad de la que ocurre en la realidad, ya que sabemos que la dupla de fuerzas longitudinales no se produce) y el módulo de corte longitudinal

Por otra parte, la deformación angular debida al mecanismo II no puede estimarse de forma tan precisa. Normalmente se asume que el módulo a torsión GT es la mitad del módulo a corte longitudinal, así es que, para el caso de que todas las láminas tengan el mismo espesor t y la sección sea rectangular, la fórmula puede simplificarse como
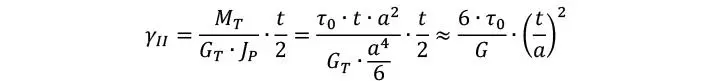
Así es que la deformación total
Y por tanto la rigidez
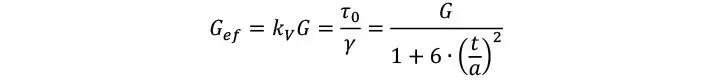
Por lo que el factor de corrección se puede estimar únicamente a partir de la esbeltez de la sección transversal de los tablones
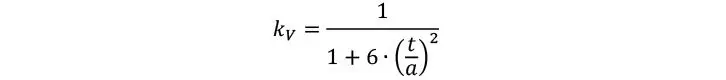
La estimación anterior sin embargo toma en cuenta el caso de que el número de láminas sea infinito. Silly realizó múltiples modelos de MEF para calcular de forma más exacta el coeficiente kV considerando diferentes números de láminas, llegando a una expresión más precisa que incluía 2 coeficientes de ajuste que dependen del número de láminas, ver valores en Tabla 1.3.7.
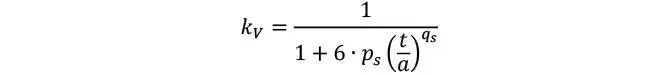
| TABLA 1.3.7 Coeficientes ps y qs para ajuste del factor de corrección de rigidez de corte en el plano según el número de láminas del CLT según el anexo nacional austriaco del Eurocódigo 5. |
| Parámetros de ajuste |
Número de laminaciones |
| 3s |
5s,7s y más |
| ps |
0,53 |
0,43 |
| qs |
1,21 |
Así es que finalmente, según el modelo de corte en el plano de Schickhofer, podemos estimar la componente de rigidez de corte de un tablero homogéneo y con espesor de láminas constante como
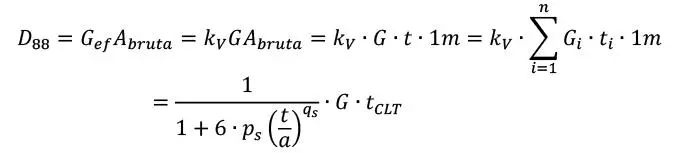
En la práctica la relación t/a suele ser entre 0,1 y 0,25 aproximadamente, por lo que, habitualmente el factor de corrección es del orden de 0,6-0,8, ver Figura 1.3.7.6.
FIGURA 1.3.7.6 Valores del factor de corrección kV en la práctica para las relaciones t/a más habituales (basado en Schickhofer et al. 2009).
1.3.8 Componentes de rigidez flexional y torsional
Se suele establecer un sistema de coordenadas z tal que z=0 en el plano intermedio, designando una zmin y zmax para cada una de las láminas tal como se muestra en la Figura 1.3.8.
FIGURA 1.3.8 Típica designación de la coordenada z de cada lámina según el plano intermedio.
De modo que las rigideces flexionales y torsionales de cada lámina pueden obtenerse escalando las rigideces de membrana según la coordenada z tal que
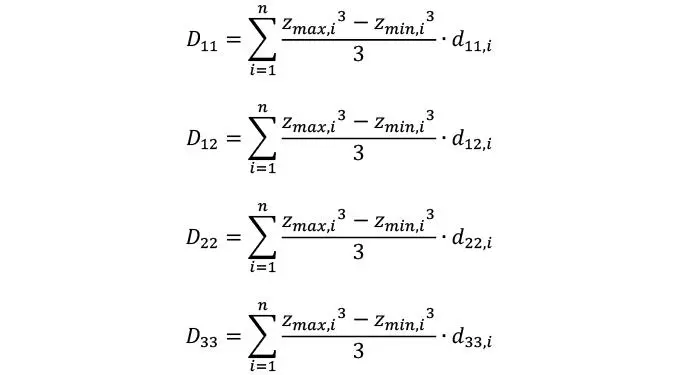
1.3.9 Factor de reducción de rigidez torsional
Читать дальше