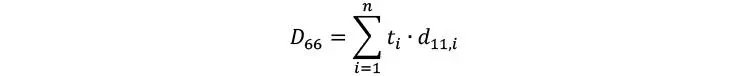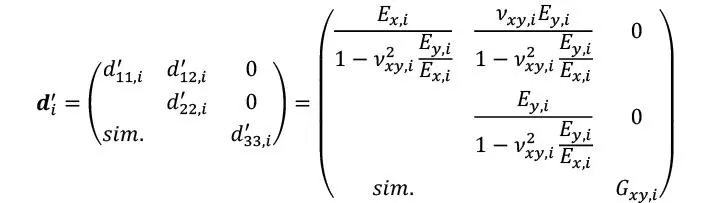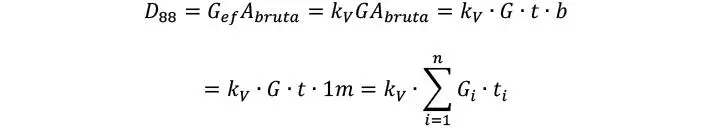Pablo Guindos - Conceptos avanzados del diseño estructural con madera

Y en el caso de que las láminas estén orientadas en múltiplos de 90° como en el CLT, la matriz de rigidez se simplifica a

Donde los términos en color verde engloban la rigidez a la flexión y torsión, los términos azules engloban el cortante transversal, los términos rojos la rigidez de la membrana y los términos naranjas son comúnmente referidos como excentricidades que acoplan las respuestas de membrana con las flexionales y torsionales. Dicho efecto de acoplamiento es muy poco aconsejable, porque provoca que los momentos provoquen no solo curvatura sino también deformaciones y distorsiones en la membrana. Asimismo, los esfuerzos puros de membrana también provocan curvaturas y torsiones. Por ello, no solo en el CLT, sino en la mayoría de compuestos laminados trata de evitarse la asimetría y el desbalanceado de los laminados; es muy recomendable que la configuración de láminas (geometría y rigideces) sea simétrica, y además cada lámina en la parte superior del plano de simetría tenga su contraparte (ángulo de orientación de fibras) en la parte inferior. No obstante, es importante notar que es posible evitar las excentricidades empleando ciertas configuraciones asimétricas también.

Observamos entonces que los únicos términos de acoplamiento remanentes resultan D12 y D67, los cuales acoplan las curvaturas y deformaciones de membrana, respectivamente, en los ejes x e y. En muchas ocasiones, se desprecian las interacciones de momentos flectores y axiles de modo que la matriz puede venir definida como

Las componentes de rigidez, lógicamente hacen referencia a las rigideces flexionales, torsionales, cortantes y axiales de la placa por lo que habitualmente

Nota: las componentes de rigidez indicadas en realidad deben partirse por unidad de ancho (ver definiciones en apartados sucesivos), pero en este libro se indican así para mejorar la comprensión.

Tal y como se introdujo con anterioridad, en la práctica es habitual emplear factores de modificación por corte transversal k, ya que en realidad las secciones no son planas, sino que experimentan deformaciones por corte tal como se ilustró en la Figura 1.3.1. También, tal como se detalla posteriormente, la rigidez torsional disminuye por el hecho de que los tablones no estén encolados en los bordes o bien puedan presentar grietas, por lo que se suele aplicar un factor de minoración kT. Finalmente, la rigidez de corte longitudinal en el plano también se reduce por la discontinuidad de los tablones en la lámina y el mecanismo de transmisión del esfuerzo de corte kV, así es que la matriz de rigidez incluyendo los factores de modificación resultaría

1.3.6 Rigidez de la membrana

Las componentes de rigidez axial y cortante longitudinal de la membrana suelen calcularse como la contribución en paralelo de cada lámina i

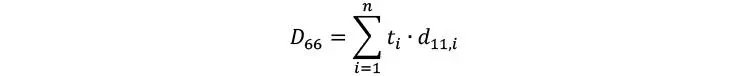
Donde las componentes de rigidez de cada una de las láminas i, lógicamente se obtienen de la matriz de rigidez de tensión plana para materiales transversalmente isótropos

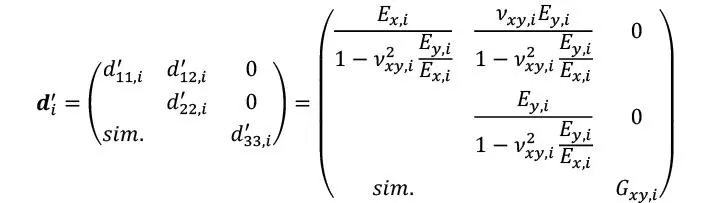
La cual debe ser pre multiplicado por la matriz traspuesta de transformación, y pos multiplicado por la matriz de transformación de acuerdo al ángulo de la lámina (βi, definido como el ángulo entre el eje x del modelo y la dirección de la fibra en la lámina i)

con

Donde c = cos(βi) y s = sen(βi), siendo βi el ángulo entre la dirección x y la dirección de la fibra de la lámina considerada.

1.3.7 Modelo de Schickhofer para reducción de rigidez de corte en el plano

Tal como se comentó anteriormente, podría pensarse que, dado que la rigidez a cortante longitudinal Gxy es transversalmente isótropa (=Gyx), en cada una de las láminas del CLT, la rigidez a cortante en el plano de la placa sería simplemente

Sin embargo, los tablones de madera que conforman cada lámina no siempre están encolados en los bordes o pueden tener grietas de secado, así que por seguridad siempre se asume que no hay continuidad en cada lámina, por lo que la rigidez al corte es significativamente menor a la que se obtendría si es que toda la madera mostrase una continuidad perfecta.

La deducción de la rigidez “efectiva” a corte en el plano de la placa del CLT, suele atribuirse al modelo presentado por Schickhofer (2009). El objetivo de este modelo consiste en determinar un factor de reducción de la rigidez por corte en la membrana, kV, que pueda emular con mayor precisión la rigidez del CLT tal que

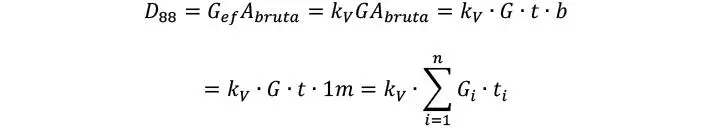
El modelo de Schickhofer, consiste en realizar una homogeneización del comportamiento a corte del CLT de modo que el Gefectivo, y por tanto el factor kV, pueda ser determinado. Para ello, primeramente, se discretiza un tablero de CLT solicitado al corte a una serie de volumenes de elemento representativo (representative volume element, RVE) los cuales, de forma individual, pueden representar adecuadamente la rigidez de cualquier tablero de CLT independientemente de sus dimensiones, ver Figura 6.1.5.7.1. La característica fundamental del RVE es que tiene un ancho a, que corresponde con el ancho de los tablones o separación entre ranuras (w1).

Posteriormente, y solo de forma imaginaria, se asume que el tablero de CLT no está compuesto por 3, 5 o 7 sino por un número infinito de láminas, lo que permite transformar el RVE a un sub-volumen de elemento representativo (representative volume sub-element RVSE), ver Figura 1.3.7.1. Esta segunda transformación se hace con el fin de independizar el problema del número de láminas y reducirlo a estudiar tan sólo la mitad del espesor de 2 láminas contiguas, ya que, si el panel fuese infinito en cuanto a número de láminas y estuviese sometido al corte en el plano, la distribución de tensiones sería simétrica en cada RVSE. Posteriormente se realiza un ajuste para el número real de láminas.

Una vez definido el RVSE, la transmisión real del esfuerzo de corte puede entenderse como la composición aditiva de dos mecanismos. Imaginemos por un lado que todos los RVSE en los que puede ser discretizado y transformado un tablero de CLT están perfectamente encolados en los bordes en cada una de las 2 láminas, y no existiese ninguna otra discontinuidad como grietas de secado, y etc. Bajo esta situación, la transmisión de corte se debería únicamente al corte puro en cada una de las láminas, lo cual es referido como el mecanismo de transmisión I. Es decir, que, si un tablero de CLT lo discretizásemos y transformásemos a una serie de RVSE, en cada uno de los RVSE observaríamos la deformación que se ilustra en la Figura 1.3.7.1 izquierda.

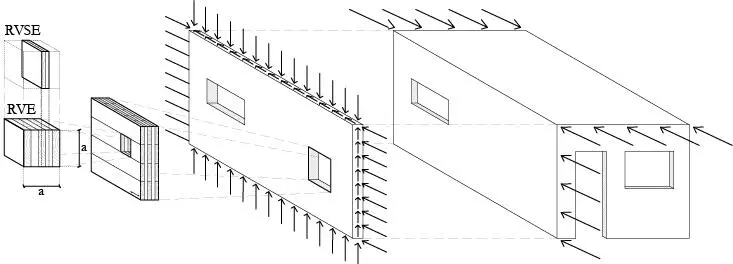
FIGURA 1.3.7.1 Ilustración de la solicitación de corte de un tablero específico de CLT, y proceso de discretización del RVE y transformación a RVSE como unidad geométrica fundamental para la teoría de Schickhofer (basado en Schickhofer et al. 2009).