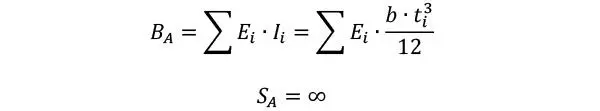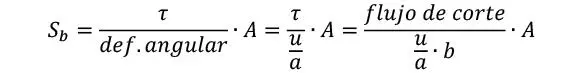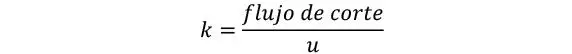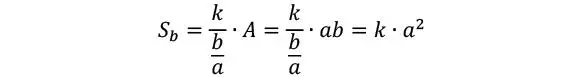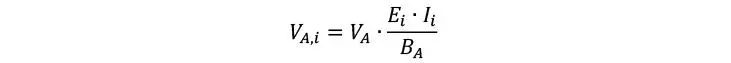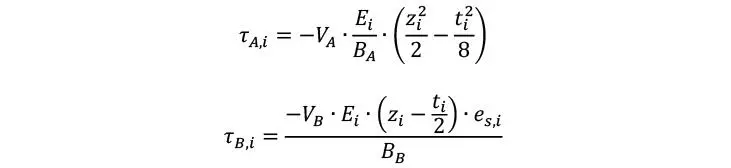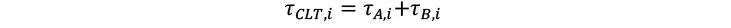Pablo Guindos - Conceptos avanzados del diseño estructural con madera

De este modo, es posible aproximar las tensiones en el CLT con la sumatoria de las tensiones A y B, ver una ilustración en la Figura 1.2.4.2.

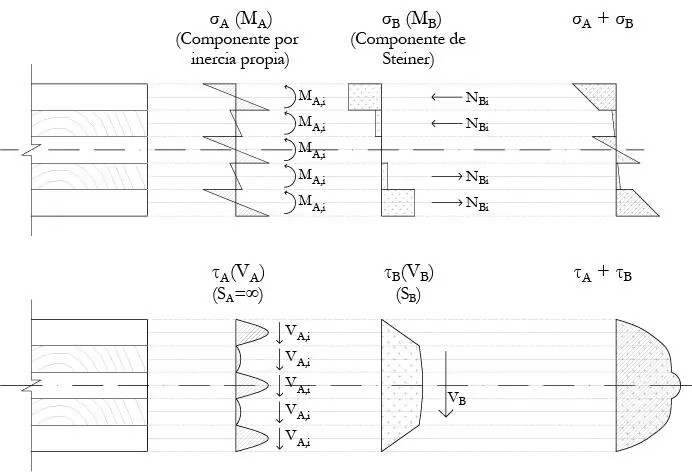
FIGURA 1.2.4.2 Sumatoria de las contribuciones de tensiones por momento flector sin acción compuesta, cordón A, y contribuciones por transmisión de flujo de corte a través de interfaz flexible, cordón B, como base para el cálculo de solicitaciones del CLT según el método de analogía de corte (basado en Bogensperger et al. 2012).

Debe notarse que el fundamento anterior es similar al pilar fundamental del razonamiento teórico del método γ. En el método γ, se asume que la semirrigidez de la unión únicamente afecta a las tensiones derivadas de la inercia adicional de la contribución de Steiner. En el método de la analogía del cort,e también se separa la componente de Steiner y únicamente allí se considera la transmisión del corte. La diferencia principal de este último método es que en lugar de considerar la semirrigidez de corte de la unión (representada por γ), se considera la flexibilidad (semirrigidez) de corte de las capas transversales por el efecto de la rodadura. Es por ello que este método se ha denominado “analogía” de corte, respecto de la semirrigidez de una unión en el método γ. Dicho efecto de flexibilidad, se considera en su totalidad en el cordón B, lo que permite modelar paneles de CLT con cualquier número de láminas y tipos de carga.

La estrategia para resolver el sistema anterior, consiste en acoplar el campo de las deflexiones de ambos cordones, y resolver la deformación por corte del cordón B. Aunque existen soluciones analíticas para lo anterior, lo habitual es aplicar programas computacionales de cálculo en el contexto de este modelo. En concreto, los paneles de CLT se suelen modelar como vigas acopladas, atribuyendo las rigideces que a continuación se detallan. Una vez calculadas los esfuerzos de corte y momentos de los cordones, se procede a determinar las tensiones internas reales aplicando una regla de transformación que a continuación se detalla. El método también es apropiado para modelar losas biaxiales.

Cálculo de rigideces y tensiones

La rigidez flexional del cordón A, es lógicamente la suma (en paralelo) de las rigideces individuales de las láminas, y la rigidez al corte se asume infinita

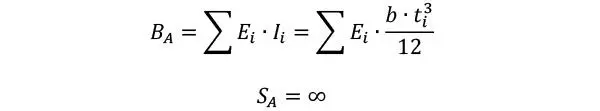
Nota: Ei suele despreciarse igualmente para las láminas perpendiculares, aunque al ser calculado mediante software en ocasiones se considera. Para la rigidez al corte en la práctica se le atribuye un valor muy elevado.

Respecto del cordón B, la rigidez flexional es la suma (en paralelo) de las componentes de Steiner, y la rigidez al corte es la suma (en serie) de las rigideces a corte de las láminas longitudinales y perpendiculares

Nótese que de igual modo la rigidez de las láminas perpendiculares no se suele contabilizar en la rigidez flexional. Respecto de la rigidez al corte, se considera, al igual que en el método γ, que la rigidez al flujo de corte de cada lámina es

Dado que las láminas se deforman en serie, ver Figura 1.2.4.3, y que las mitades exteriores de las láminas externas no se deforman (y por tanto su rigidez a corte no contribuye), la rigidez equivalente al flujo de corte resulta

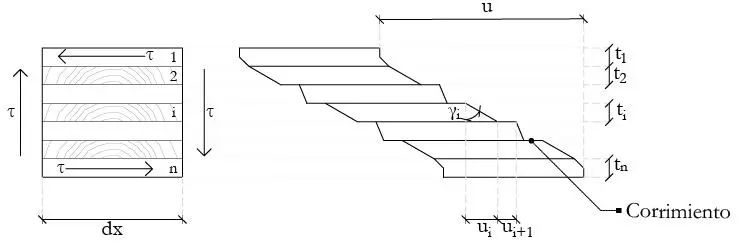
FIGURA 1.2.4.3 Deformación en serie al cortante de las láminas de CLT (readaptado para el CLT a partir de consideraciones en DIN1052 2010).

Considerando que solo se produce deformación por corte entre los centros de gravedad de las láminas externas del CLT (distanciadas a una distancia a), la rigidez al corte del cordón B, que a su vez representa la rigidez al corte de la “viga” de CLT puede estimarse como

Tal que

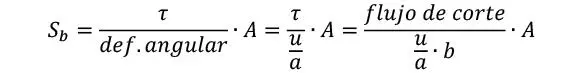
Dado que

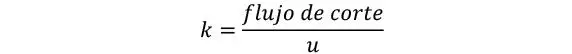
Se obtiene

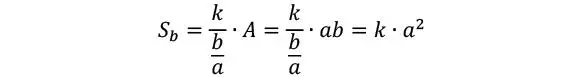
Así es que

Una vez calculados los esfuerzos en el programa computacional de acuerdo a las rigideces anteriormente comentadas, se pueden estimar el reparto de momentos y axiles en cada una de las láminas sin más que relativizar las rigideces flexionales y axiales respectivamente

Los que permiten estimar las tensiones flexionales en cada punto de la sección vertical (z)

Por supuesto las tensiones axiales se pueden estimar de acuerdo a la posición del cdg de cada lámina (es,i)

Y naturalmente, la tensión axial real en cualquier punto de la sección se aproxima como

Por otra parte, el cortante A se reparte en las láminas según rigidez flexional

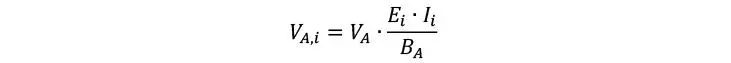
Y el cortante B no requiere transformación porque ya considera la rigidez al corte del CLT. Finalmente, las tensiones de corte se pueden aproximar como

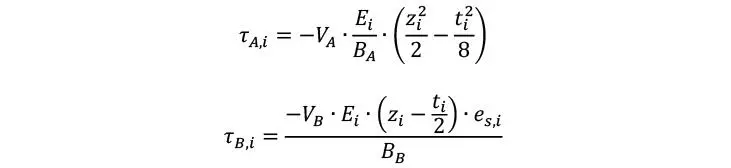
De modo que

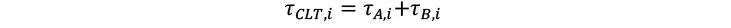
Ventajas y desventajas del método

Ventajas: puede modelar cualquier cantidad de láminas y tipo de cargas con gran exactitud. Sin duda, es capaz de aproximar la solución de vigas continuas de forma mucho más exacta que los otros 2 métodos. Estas ventajas han hecho que el método de la analogía de corte esté siendo el método mayormente adoptado en la normativa actual.

Desventajas: su implementación requiere bastante esfuerzo, y requiere un mayor grado de discretización que los métodos anteriores. Las tensiones de corte no se aproximan bien en áreas cercanas a cargas puntuales y apoyos intermedios en vigas continuas.

1.2.5 Teoría de componentes (k-method)

La teoría de componentes, también denominada como método k, fue propuesta en algunos textos iniciales para calcular el CLT debido a que este método ya fue propuesto hace varias décadas por Blass y Fellmoser para el cálculo del terciado. La ventaja central del método, es que permite reducir el problema a la determinación de factores de modificación de rigidez y resistencia lo cual hace su aplicación muy sencilla en el cálculo. Lo anterior no solo concierne a la flexión fuera del plano, sino en realidad muchos de los principales esfuerzos, por lo que en esta sección se presenta no solo el modelo de flexión sino el modelo estructural para diferentes esfuerzos. El método se puede aplicar además para CLT de múltiples láminas. Sin embargo, la teoría de componentes tiene una limitación tremendamente restrictiva para el CLT, y es que no considera la deformación por corte. Esto se debe a que naturalmente el método fue ideado para calcular terciado donde las razones L/t suelen ser ≥ 30. Así es que la aplicación práctica en el CLT es muy reducida. No obstante, a continuación, ser resume de forma muy concisa las suposiciones y los fundamentos de este método: