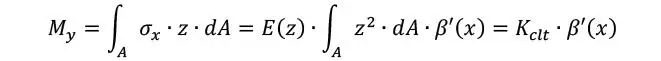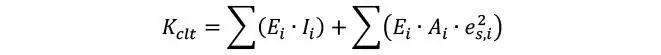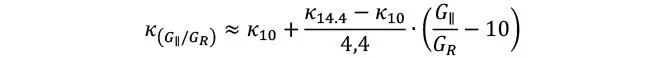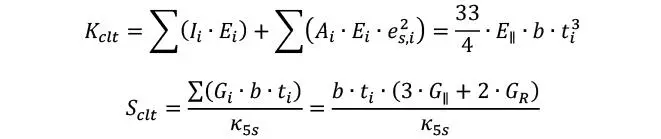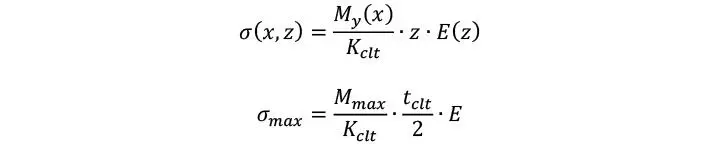3 La tensión por corte se obtiene del equilibrio local de corte y momentos de una rebanada de la viga.
Formulación básica
Asumiendo x como dirección longitudinal, y z como la dirección vertical de la sección de la viga, puede relacionarse la tensión axial con el momento flector como
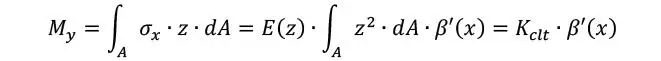
Donde β’ es la derivada del giro sobre x. Así es que la rigidez flexional del CLT, KCLT, se podría estimar en la teoría de Timoshenko, multiplicando el momento de inercia de cada una de las láminas por su correspondiente módulo elástico.
Por otra parte, la deducción del cortante, resultaría análogamente
Donde w’ es la flecha de la viga. Aunque en principio según la teoría de la viga flexible de Timoshenko se puedan incorporar diferentes módulos de cortante, uno para cada lámina, las secciones siguen permaneciendo planas, por lo que la deformación de corte se infravalora. Por este motivo, es necesario corregir la deformación por corte mediante un factor k que en la práctica divide la rigidez de corte por factores entre 3 y 6, incrementando substancialmente así la deformación
Donde K es el factor de ajuste de la rigidez cortante por tener láminas de rodadura.
Deducción de rigideces
La rigidez flexional se obtiene por simple teorema de Steiner a partir de la rigidez flexional de cada lámina como
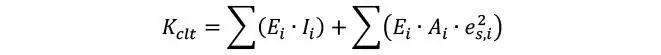
Donde lógicamente, Ei es el módulo elástico de cada lámina (nulo para láminas perpendiculares), Ai e Ii son las inercias de cada una de las láminas longitudinales y es,i es la distancia del centro de gravedad de cada láminas longitudinales no centrales a la fibra neutra. Nótese, por lo tanto, que se asume un E90 = 0, así es que en realidad KCLT se obtiene únicamente aplicando el teorema de Steiner con las láminas longitudinales no centrales, y la suma de la inercia flexional de la lámina central.
La rigidez al cortante se obtiene deduciendo directamente la deformación por corte mediante el principio de fuerzas virtuales. La expresión resultante es relativamente compleja, por lo que se suele trabajar con tablas o gráficos. Así, por ejemplo, para el caso de que los espesores de las láminas sean todos idénticos, se puede determinar k mediante la siguiente expresión para cualquier relación entre la rigidez del cortante longitudinal y la de rodadura
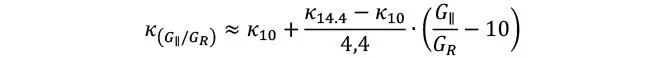
Donde los factores de corrección más típicos, para relaciones entre G/Grod de 10, 14.4 y 13.8, que además se requieren para determinar k para cualquier relación según la ecuación anterior, se detallan en la Tabla 1.2.2.
| TABLA 1.2.2 Valores de corrección de rigidez de corte por no planicie de secciones debido a la flexibilidad de la rodadura, k, en la aplicación de la teoría de viga flexible de Timoshenko para el CLT. Los valores se presentan para diferentes relaciones de la rigidez cortante G/Grod (relaciones de 10, 13.8 y 14.4, para otras relaciones es necesario aplicar la ecuación antrerior) y para diferente número de laminaciones del CLT (basado en de Bogensperger et al. 2012). |
| Número de laminaciones |
Relación rigidez de cortante G/Grod |
| k10 |
k13.8 |
k14.4 |
| 3 |
4,854 |
6,468 |
6,723 |
| 5 |
4,107 |
5,441 |
5,652 |
| 7 |
3,873 |
5,116 |
5,313 |
Por otra parte, en caso de que las láminas transversales y longitudinales del CLT no todas las laminaciones tengan el mismo espesor, es necesario aplicar un factor de corrección al propio k. Este factor depende principalmente de la relación entre el espesor medio de las láminas longitudinales (tL), y el espesor medio de las láminas perpendiculares (tQ)
En el caso de que el espesor sea constante, i.e. tL/tQ = 1, el factor de corrección por espesor de lámina es 1, es decir la rigidez es mínima, mientras que para cuando la relación de espesores es dispar, entre 0,5 y 2, la rigidez de corte se incrementa (k disminuye). La variación del factor de corrección por espesor de lámina para diferentes relaciones de tL/tQ en el caso de CLT de 5 láminas, se muestra en la Figura 1.2.2.1. Asimismo, valores típicos del factor k para diferentes configuraciones se proporcionan en el Anexo C5.
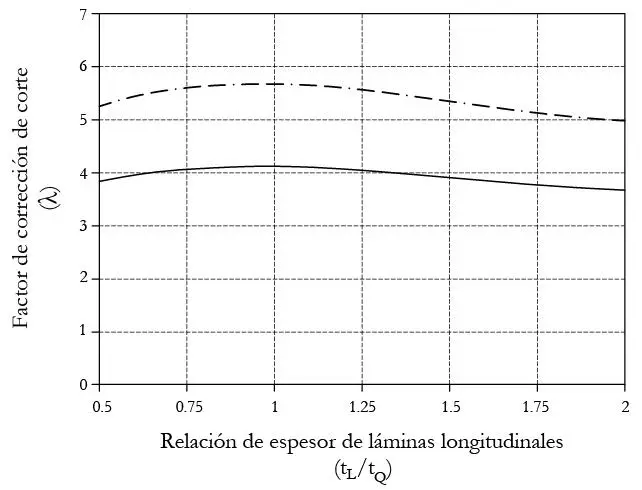
FIGURA 1.2.2.1 Efecto de la relación de espesor de láminas longitduinales y perpendiculares, tL /tQ , en el valor del factor de corrección de rigidez por no planicie de secciones k (basado en Bogensperger et al. 2012).
Finalmente, una vez determinado el factor k, se determina la rigidez efectiva de corte como
Nótese que, a diferencia de la rigidez flexional, la rigidez al corte de las láminas perpendiculares, Grod, no se desprecia y sí tributa en la fórmula anterior.
Para el caso especial de que todas las láminas se fabriquen con el mismo material y tengan el mismo espesor, pueden emplearse las siguientes fórmulas simplificadas para el cálculo de la rigidez flexional y cortante
3Láminas
5Láminas
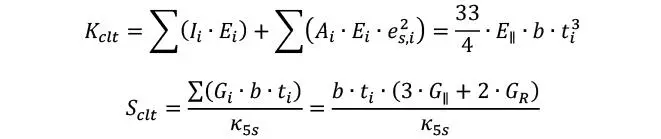
7Láminas
Determinación de las tensiones
La típica distribución de tensiones de este modelo, se ilustra en la Figura 1.2.2.2. Dado que la rigidez axial de las capas perpendiculares se asume nula, no existen tensiones en las láminas perpendiculares, lo cual se aproxima a lo que sucede en la realidad, ya que las tensiones axiales en las láminas perpendiculares son ínfimas. Obviamente, bajo estas circunstancias la tensión axial de flexión en cualquier punto de la sección, y la tensión máxima se puede calcular como
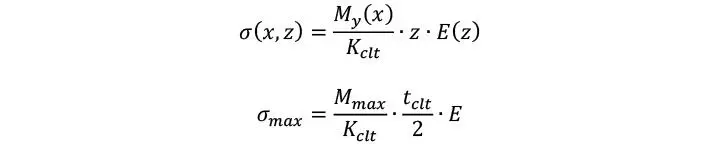
Por otra parte, en el caso de las tensiones cortantes, la contribución del primer momento estático de área de cada una de las láminas se escala de acuerdo a la relación de rigidez Ei/KCLT, así es que las láminas perpendiculares no tienen ninguna contribución en el incremento de las tensiones tangenciales. Sin embargo, a diferencia de las tensiones normales, el momento estático de las láminas longitudinales más alejadas de la fibra neutra “sigue contribuyendo”, o dicho de otra forma, la diferencia del momento flector en las láminas longitudinales sigue produciendo la misma tensión cortante en las láminas perpendiculares, así es que las tensiones cortantes de rodadura en las láminas perpendiculares se corresponden con la tensión de cortante longitudinal adyacente en las láminas longitudinales vecinas (y puede calcularse como tal), ver Figura 1.2.2.2.
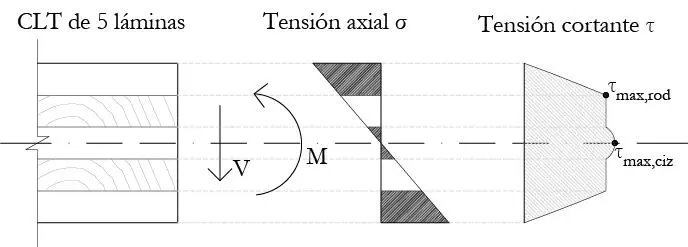
FIGURA 1.2.2.2 Típica distribución de tensiones axiales y cortantes en un panel de CLT bajo el modelo de viga flexible de Timoshenko.
Читать дальше