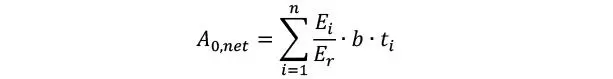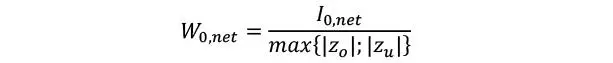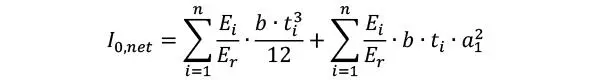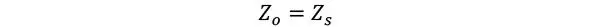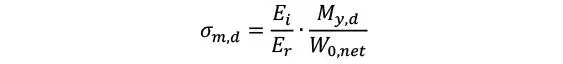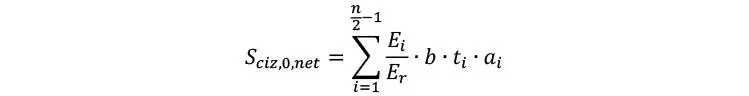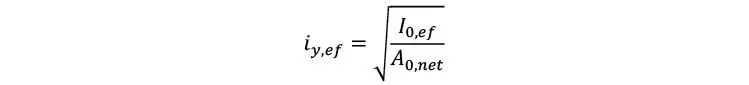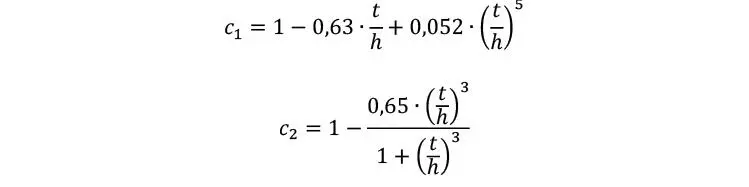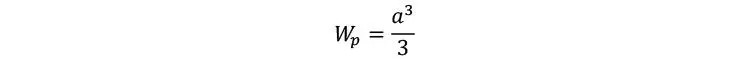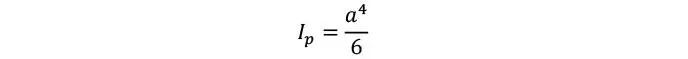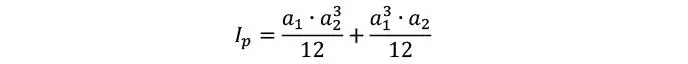Pablo Guindos - Conceptos avanzados del diseño estructural con madera

Por otra parte, para placas biaxiales, o bien cuando los esfuerzos y condiciones de contorno son relativamente complejas, suele aplicarse directamente una teoría de placas, así es que el CLT deja de simplificarse como un elemento 1D para constituir un elemento 2D.

A continuación, se resumen las características de los modelos de vigas en flexión que más se han popularizado en los códigos de diseño estructural y la práctica profesional, pero antes se resume brevemente el cálculo de los valores seccionales característicos. En el Anexo C5 se proporcionan diversos valores seccionales y mecánicos típicos, para facilitar el cálculo del CLT como elementos tipo viga.

1.2.1 Valores seccionales

Centro de gravedad de la sección

Normalmente el CLT es simétrico en espesor y rigidez de láminas, por lo que el c.d.g coincide con el centro de simetría. Sin embargo, en caso de que no fuese simétrico, o bien en caso de exposición al fuego en alguna de sus caras, el c.d.g puede variar su posición. En estos casos, el c.d.g. puede determinarse mediante el siguiente procedimiento:

1 Determinar el módulo elástico de referencia, Er.

2 Determinar la posición del c.d.g. de cada una de las láminas longitudinales respecto de la cara superior, oi, ver Figura 1.2.1.1.

3 Determinar la posición del centro de gravedad respecto de la cara superior, zs.

4 Determinar la distancia de los c.d.g. de cada lámina respecto del c.d.g. de la placa, ai.

FIGURA 1.2.1.1 Nomenclatura en la sección para la determinación del c.d.g. de la placa (basado en Wallner-Novak et al. 2013).

Nótese que lógicamente las capas perpendiculares se desprecian dado que habitualmente E⊥ = E90 = 0.

Área neta

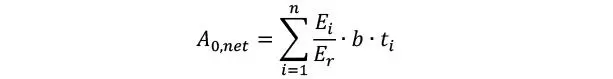
Momento resistente

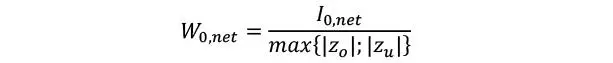
Donde la inercia de la sección neta

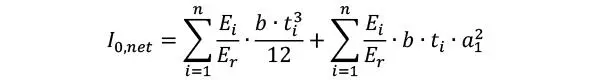
Siendo

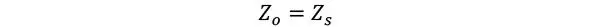
Así, la tensión flexional en cada lámina puede escalarse como

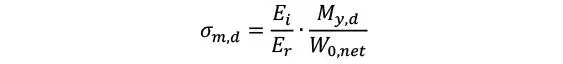
Momento estático

Cuando se aplica un cortante transversal sobre el CLT, es posible que las láminas perpendiculares a la flexión fallen por rodadura, o bien que las láminas paralelas fallen por corte longitudinal. Lo más común, es que las láminas externas se orienten con el eje de la flexión, en cuyo caso, el momento estático para la verificación a rodadura, es el momento estático de la lámina más externa hasta la lámina inmediatamente anterior a la lámina intermedia (recordemos que la distribución de corte en las láminas de rodadura es constante). Así es que el momento estático para las láminas de rodadura resulta

Donde n/2-1 representa que el cálculo del momento estático se lleva a cabo desde la lámina superior (o inferior), hasta la lámina inmediatamente anterior a la lámina central. Por otra parte, para la verificación de corte longitudinal, el corte máximo suele producirse en la lámina media que suele estar orientada longitudinalmente, así es que el momento estático correspondiente se calcula como la contribución de todas las láminas superiores o inferiores más la mitad de la lámina intermedia:

Si es que la lámina central no fuese longitudinal, el momento estático para el cizalle resultaría en el caso más común

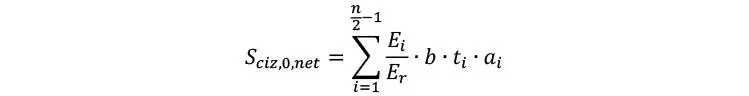
Radio de giro

Para algunas verificaciones de inestabilidad es necesario calcular el radio de giro. Habitualmente este valor se determina empleando el área neta y la inercia efectiva (que habitualmente se determina mediante el método gamma, tal como se describe en la Sección 1.2.3), tal que

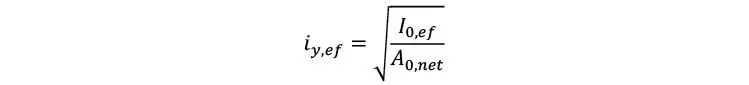
Las verificaciones de inestabilidad, son casi siempre realizadas considerando únicamente la posibilidad de pandeo fuera del plano de la placa (eje y). Las verificaciones de pandeo respecto del eje z (pandeo en el plano de la placa) solo se consideran cuando el ancho de la placa (h)

Módulo resistente de torsión e inercia torsional de la sección transversal

Según Silly (2010), para secciones rectangulares y homogéneas (láminas de idéntica calidad) puede estimarse como

Con

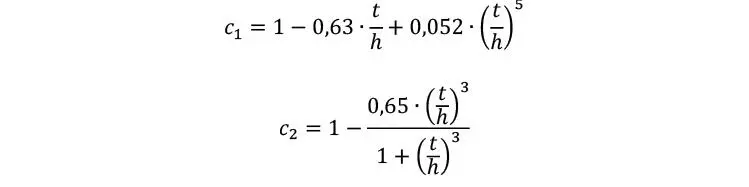
En el caso de emplear vigas de CLT esbeltas solicitadas en el canto, puede emplearse la siguiente estimación de la inercia torsional para la verificación de vuelco lateral torsional

Módulo resistente polar y momento polar de inercia del área encolada entre tablones

Tal como se detalla en secciones sucesivas, un posible mecanismo de fallo por corte, es la torsión interlaminar en las proximidades del encolado entre láminas. En la mayoría de ocasiones, las láminas emplean tablones del mismo ancho a por lo que la superficie interlaminar sometida a torsión tiene una forma cuadrada. Además, se suele asumir que las tensiones cortantes se distribuyen linealmente. Bajo estas circunstancias, el módulo resistente polar se puede estimar como

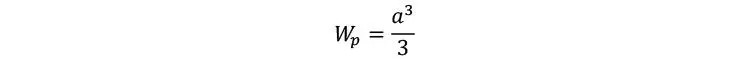
Y el momento de inercia polar resulta

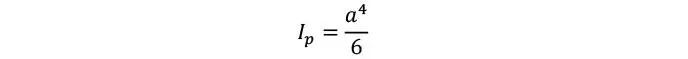
En caso de que la superficie no sea cuadrada sino rectangular, de área a1 · a2 (siendo este último el lado más corto) el módulo polar puede estimarse como

Mientras que la inercia polar resulta

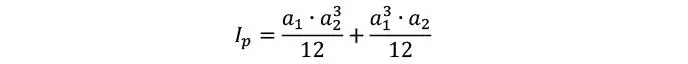
1.2.2 Modelo de viga flexible de Timoshenko

El modelo de viga flexible de Timoshenko es un método analítico relativamente sencillo que permite predecir las tensiones y deformaciones de losas uniaxiales, y en general cualquier elemento tipo placa que esté principalmente solicitado en una dirección de flexión fuera del plano. Este método consiste en idealizar la tensión y deformación de la losa como una viga flexible. Se construye asumiendo las siguientes suposiciones:

1 La sección no es perpendicular a la deformada elástica, pero permanece plana.

2 Pese a que contradiga lo anterior, se asume que la sección adquiere curvatura debido al corte. Esto se logra aplicando un factor de corrección por corte K, lo que permite calcular más adecuadamente la rigidez, tensión y deformación por corte.