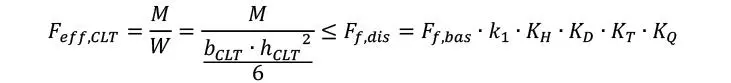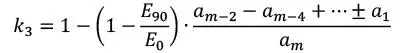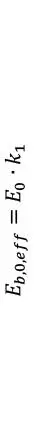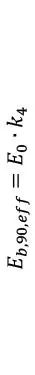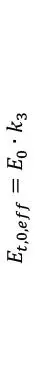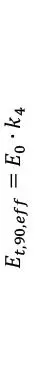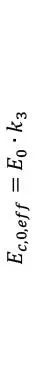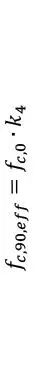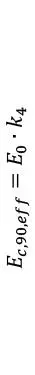Pablo Guindos - Conceptos avanzados del diseño estructural con madera

Hipótesis de Bernouilli sobre planicie de secciones deformadas. No existe deformación cortante porque la relación L/t ≥ 30.

La rigidez perpendicular no es 0 sino E⊥=E90= E||/30= E0/30.

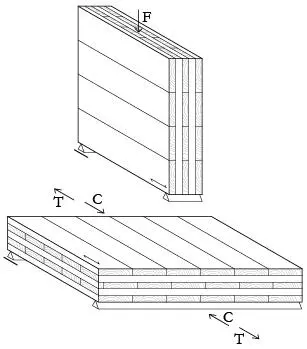
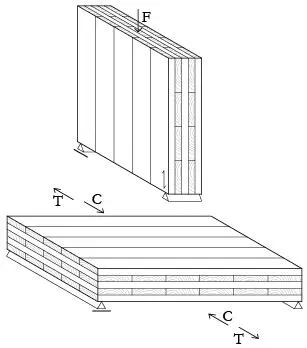
La rigidez efectiva del CLT para diferentes estados de carga, puede calcularse como el producto de la rigidez E0 multiplicada por el coeficiente de modificación de rigidez, ki, correspondiente, ver Tablas 1.2.5-6.

La resistencia efectiva (tensiones admisibles) del CLT para diferentes estados de carga, también pueden calcularse considerando el producto de la resistencia (tensión admisible) multiplicada por el coeficiente de modificación correspondiente, ki, ver Tabla 1.2.6.

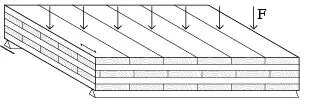
Una vez modificadas las rigideces efectivas, las rigideces flexionales y las solicitaciones pueden calcularse empleando inercias, áreas y módulos resistentes brutos sin considerar el efecto de la ortotropía de las capas. Por ejemplo, el cálculo de la rigidez flexional resulta

y

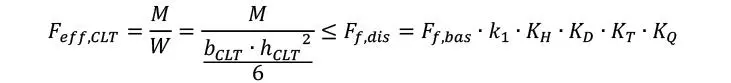
TABLA 1.2.5 Determinación de los coeficientes de modificación ki según el estado de carga para la aplicación del método k (modificado de Gagnon y Popovski 2011).

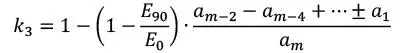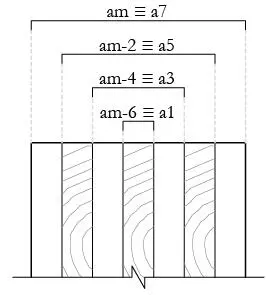
TABLA 1.2.6 Aplicación de los coeficientes de moficidación ki para el cálculo de tensiones admisibles y rigideces efectivas del CLT según el método k (después de Gagnon y Popovski 2011).
Solicitación	Orientación fibra externa respect solicitación	Resistencia efectiva	Rigidez efectiva
Fuerzas fuera del plano
Flexión	Paralela
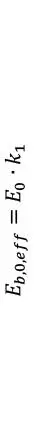Perpendicular
Fuerzas en el plano
Flexión	Paralela
Perpendicular
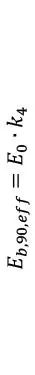Tracción	Paralela
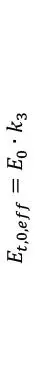Perpendicular
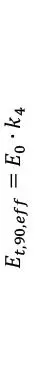Compresión	Paralela
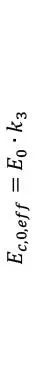Perpendicular

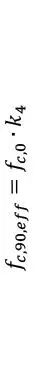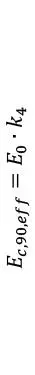1.3 MODELO DE CÁLCULO TIPO PLACA; TEORÍA DE PLACAS CON CONTRIBUCIÓN DE CORTE DE PRIMER ORDEN

A pesar de que varios de los modelos de vigas anteriores pueden extenderse con mayor o menor dificultad para constituir elementos tipo placa (2D) y poder modelar así flexiones biaxiales, así como otras situaciones de carga y condiciones de vínculo más complejas, sin duda la forma más extendida para modelar este tipo de elementos, especialmente cuando las condiciones de carga, vínculo y geometrías son complejas, consiste en emplear directamente un modelo de placa, referido habitualmente como plate (sin esfuerzos de membrana) shell, (con esfuerzos de flexión y membrana) en contextos de modelos computacionales. Estos modelos no sólo se aplican para predecir la flexión fuera del plano, sino que en general se usan para explicar prácticamente todo el comportamiento mecánico del CLT.

Pese a que existen soluciones analíticas, especialmente para situaciones de carga y vínculo relativamente sencillas, claramente la resolución de problemas con elementos 2D suele realizarse mediante métodos numéricos de aproximación. En particular, es muy común emplear el modelo de los elementos finitos (MEF) para aproximar soluciones, y es por ello, que en la práctica profesional el uso del término plate o shell suele relacionarse con el MEF. La precisión de estos modelos es sin duda muy superior a los modelos analíticos (o eventualmente computacionales como, por ejemplo, la analogía de corte) anteriormente descritos. De hecho, a menudo el “error” de los modelos de flexión uniaxial presentados anteriormente, se determina en función de cuan bien pueden estos emular los resultados del modelo que a continuación se describe.

Sin duda la teoría de placas es extensísima entre otras cosas porque permite predecir la rigidez, deformación y tensiones internas de elementos tipo placa compuestos por capas laminadas reduciéndolos de 3D a 2D. Cada una de las láminas puede ser isótropa, transversalmente isótropa u ortótropa. Esto es particularmente importante para la industria aeroespacial, que convencionalmente fabrica las cáscaras o “shells” de naves con placas compuestas laminadas. Por supuesto el análisis de la teoría de shells no es el objeto de este libro, por lo que a continuación se describe únicamente lo esencial en relación a la modelación del CLT.

Principalmente existen 2 teorías para simplificar el comportamiento global de placas compuestas laminadas, tales como el CLT a elementos 2D, y afortunadamente, muchos de los softwares comerciales mayormente empleados permiten implementar ambos modelos:

1 Teoría clásica de placas laminadas o teoría de laminados basada en la teoría de placas de Kirchhoff (teoría clásica de laminación). Usualmente empleada para predecir el comportamiento de placas delgadas, asume que el plano intermedio en el plano de la placa es el plano neutro (similar a fibra neutra en la teoría de vigas), por lo que no existen ni deformaciones ni tensiones. Tampoco considera que pueda existir tensión y deformación en la dirección del grueso de la placa. Finalmente asume que las secciones de la placa son planas y perpendiculares al plano intermedio, es decir, que no existe deformación por corte.

2 Teoría de placas laminadas con contribución de corte o teoría de laminados basada en la teoría de placas de Mindlin (teoría de cortante de primer orden). Es similar a la teoría clásica de Kirchhoff, pero sí considera la deformación por corte lo que la hace mucho más conveniente para predecir el comportamiento de placas gruesas tales como el CLT en su morfología más habitual.