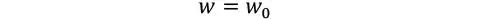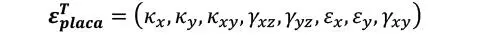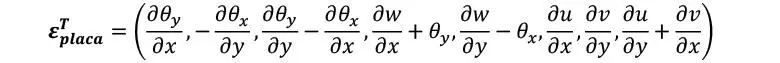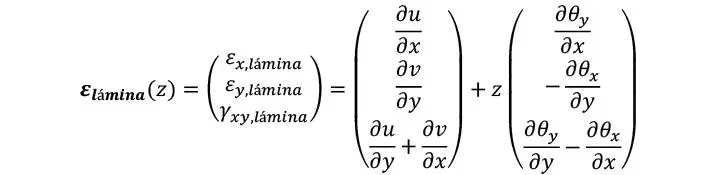Pablo Guindos - Conceptos avanzados del diseño estructural con madera

Por lo anterior, a continuación, se resumen las particularidades del modelo de laminado basado en la teoría de placas de Mindlin para aplicación en el CLT y, se explican los modelos actuales de cálculo empleados para determinar las diferentes rigideces.

1.3.1 Suposiciones fundamentales de la teoría de placas de Mindlin

Al igual que en la teoría de Kirchhoff, el plano intermedio se asume como el plano neutro, y también se considera que no existe deformación en el grueso de la placa εz=0, es decir se asume la hipótesis de tensión plana. Esto se adapta bastante bien a la realidad, si es que la geometría no se acerca a la de un sólido (l/t<10).

Además, tal y como fue introducido con anterioridad, la sección perpendicular de la placa permanece plana y de espesor constante, pero no necesariamente perpendicular a la deformada. Dicho de otro modo, se permite que haya deformación por corte transversal, tal que las normales a la placa no resultan perpendiculares al plano intermedio, ver Figura 1.3.1. Así pues, la deformación de corte se asume constante en toda la placa, lo que obliga a emplear factores de corrección de deformación por corte transversal, k. Además de ello, tal como se detalla en apartado sucesivos, también se suele requerir la aplicación de factores de corrección por torsión y corte longitudinal, k.

FIGURA 1.3.1 Deformación básica y desplazamientos en la teoría de placas de Mindlin: (izquierda) el giro de la sección plana se asume como la suma del giro debido a la deformada más la contribución del corte, lo que contrasta frente a la sección no plana real; (derecha) los desplazamientos horizontales se asumen como la sumatoria del desplazamiento de la deformada en el plano intermedio más la contribución por giro (basado en Oñate 2013).

1.3.2 Formulación de desplazamientos en la teoría de Mindlin

El desplazamiento horizontal de cualquier punto de la placa se asume como una composición del desplazamiento de la lámina intermedia (u0 y v0, medidos en z=0), menos el desplazamiento horizontal correspondiente al giro (sobre ejes x e y) multiplicado por el ángulo de giro (θ). Nótese que, como se asumen pequeños desplazamientos, y las secciones permanecen rectas, el desplazamiento horizontal debido al giro puede calcularse como el producto de la coordenada z (radio) multiplicado por el ángulo de giro θ, ver Figura 6.1.4.5.1.

A su vez, tal como se muestra en la Figura 6.1.4.5.1, el giro sobre cualquiera de los dos ejes se asume como la suma del giro provocado por la rotación de la normal en estado deformado, más la rotación debido al corte:

Finalmente, se asume que la sección no se deforma en su espesor, por lo que el desplazamiento vertical de cualquier punto de la sección transversal se asume idéntico al desplazamiento del plano intermedio

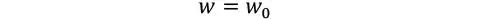
1.3.3 Deformaciones

Dado que la matriz de rigidez del elemento de CLT con capas simétricas es casi diagonal, puede establecerse una relación bastante directa entre los esfuerzos y las deformaciones, así como los dos acoplamientos anteriormente mencionados:

Los momentos mx, my y mxy son, respectivamente, los principales causantes de las curvaturas (giros por unidad de longitud) de kx, ky y kxy.

Los cortantes transversales vx e vy provocan distorsiones verticales en cada uno de los planos ortogonales de la placa, γxz, γyz.

Los axiles y el cortante en la placa nx, ny y nxy son, respectivamente, los principales causantes de las tensiones y distorsión angular en la membrana εx, εy, γxy.

El vector traspuesto de deformación global de la placa puede escribirse como

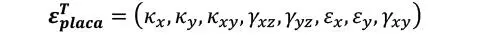
O lo que es lo mismo

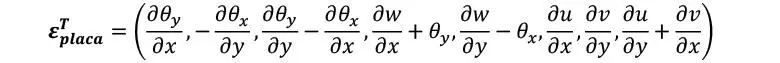
De modo que, análogamente a la formulación de desplazamientos, la deformación individual en cada coordenada vertical z de cada lámina suele calcularse a partir de las deformaciones globales de la placa como

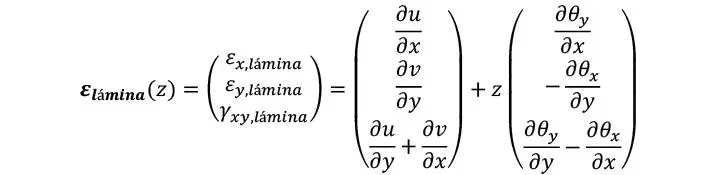
Nótese que en esta última ecuación no se considera explícitamente la contribución de la deformación por corte transversal en la lámina. Esto se debe a que, si bien dicha contribución si se toma en cuenta en la deformación de la placa para las verificaciones de servicio, no se suele incorporar en la deformación de las láminas individuales porque las tensiones cortantes perpendiculares suelen considerarse independientemente, es decir, no se calculan a partir de las deformaciones de las láminas individuales, ver Sección 1.3.11.

1.3.4 Esfuerzos y tensiones en la placa

Los esfuerzos internos, i.e. axiles, cortantes y momentos, a los que la placa está sometida se asumen esfuerzos por metro de ancho (kN/m y kNm/m, respectivamente) por lo que la denominación suele ser con letras minúsculas. La dirección del largo, x, se toma como la dirección de la fibra en el exterior de la placa, y el ancho, y, es la dirección perpendicular al largo en el plano de la placa. La convención de signos y direcciones de los esfuerzos internos es similar a la que se emplea en el hormigón, ver Figura 6.1.5.3; el primer subíndice hace referencia al eje normal al plano en el que actúa el esfuerzo, el segundo subíndice hace referencia a la dirección donde se producen las tensiones. En caso de que los dos subíndices se repitan, se elimina uno de los subíndices. Por ejemplo, el axil por metro de ancho nx representa un esfuerzo que actúa en el plano cuya normal es el eje x y produce tensiones de dirección x. El esfuerzo nxy es el esfuerzo que actúa en el plano cuya normal es el eje x, pero produce tensiones de dirección y. En total, la placa puede estar sometida a los siguientes esfuerzos:

1 Fuerzas axiales por unidad de longitud en las 2 direcciones horizontales, nx y ny, que generan tensiones axiales σx, σy en la membrana, esto es en el plano de la placa, ver Figura 1.3.4.

2 Momentos flectores por unidad de longitud respecto de ambos ejes, mx y my, que generan tensiones σx, σy en la membrana.

3 Momento torsor (twisting) por unidad de longitud. El momento actúa en el plano cuya normal es x y produce tensiones cortantes en el eje y por lo que la designación es mxy y τxy. Por supuesto se genera un momento idéntico en el plano con normal y que produce esfuerzos tangenciales en x.

4 Cortante por unidad de longitud en el plano de la placa, nxy, que generan tensiones cortantes en el plano de la placa τxy.

5 Cortantes por unidad de longitud perpendiculares al plano de la placa, en los planos xz e yz, vx y vy, que generan tensiones cortantes en ambos planos perpendiculares a la placa τxz, τyz.

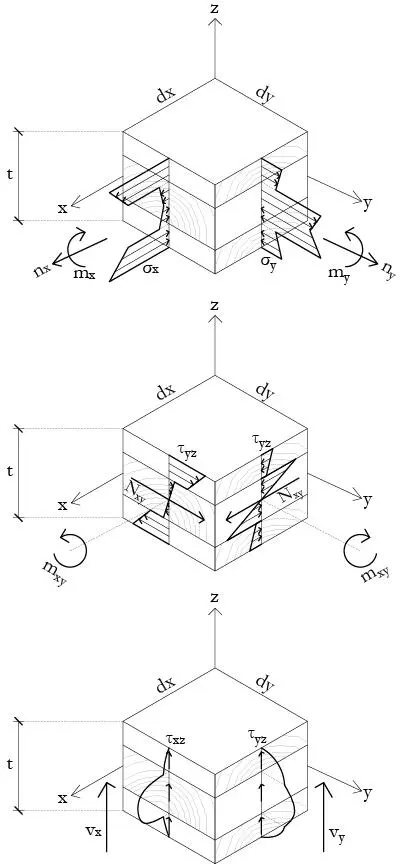
FIGURA 1.3.4 Esfuerzos y tensiones en la placa.

1.3.5 Matriz de rigidez del elemento

La matriz de rigidez de la placa puede definirse como