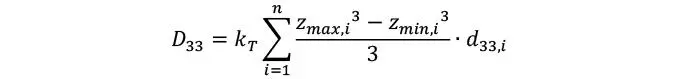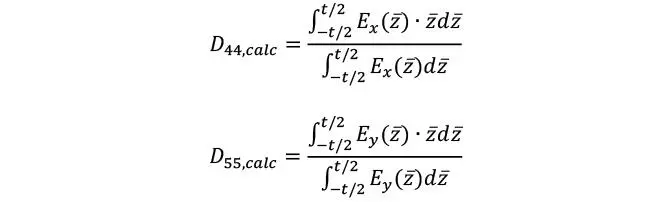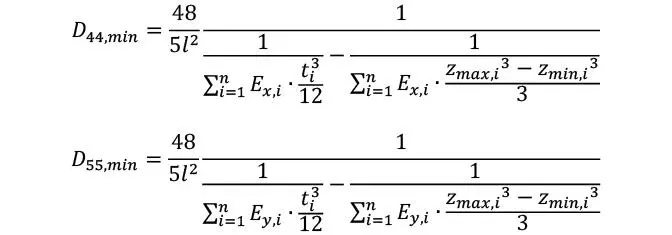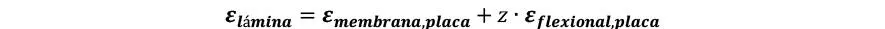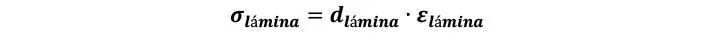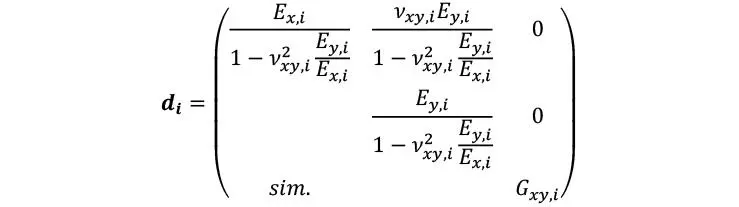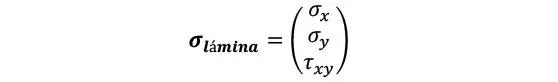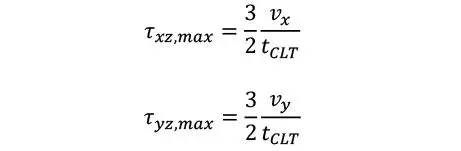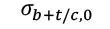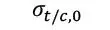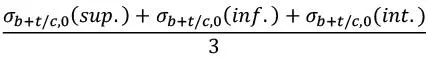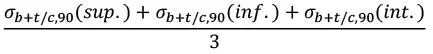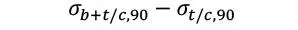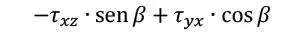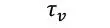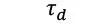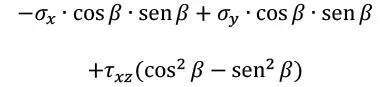La última ecuación para el cálculo de la rigidez torsional D33, implica que la rigidez torsional es proporcional al módulo elástico Gxy, es decir el módulo de corte en el plano de la placa = Glongit = G0. Tal como se mostró para la rigidez de cortante en la membrana esto no es cierto, ya que no podemos asumir que los tablones están encolados en los bordes sin ninguna grieta. Como ya se comentó, asegurar esto es imposible por lo que generalmente se aplica un factor de corrección de la rigidez de torsión kT, lo que permite adecuar la flexibilidad que se observa en la práctica, ver una ilustración de la típica deformación torsional en la Figura 1.3.9.
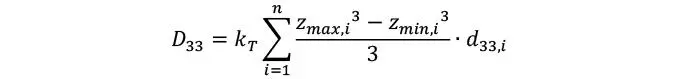
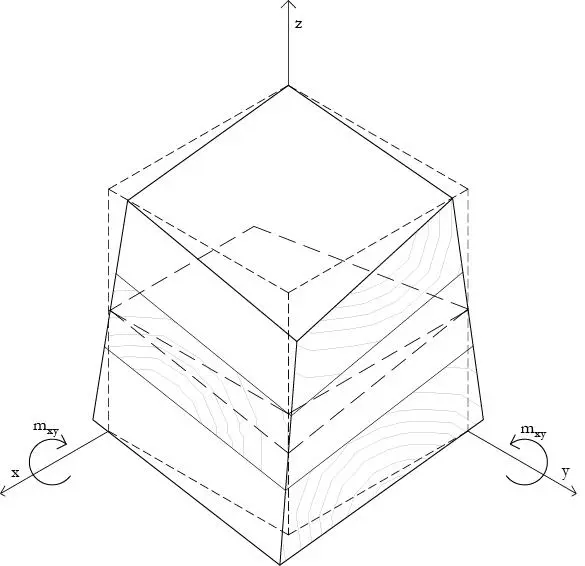
FIGURA 1.3.9 Típica flexibilidad torsional derivada de la falta de continuidad de los tableros en los bordes (basado en Silly 2010).
De hecho, Silly (2010) demostró que es posible ajustar la rigidez torsional de forma prácticamente idéntica a la rigidez de cortante en la membrana, con la diferencia de que los parámetros de ajuste eran diferentes, ver valores de ajuste según el número de láminas en la Tabla 6.1.5.9.
| TABLA 6.1.5.9 Coeficientes pT y qT para ajuste del factor de corrección de rigidez de torsión según el número de láminas del CLT de acuerdo al anexo nacional austriaco del Eurocódigo 5. |
| Parámetros de ajuste |
Número de laminaciones |
| 3s |
5s |
7s y más |
| pt |
0,89 |
0,67 |
0,55 |
| qt |
1,33 |
1,26 |
1,23 |
1.3.10 Componentes de rigidez de cortante transversal
El cálculo de este parámetro es relativamente complejo debido a que es bastante habitual corregir la rigidez de corte debido a que en realidad la sección no permanece plana; es decir, se asume que existe una tensión de corte constante cuando es conocido que en realidad esto no es así. Para el caso de vigas rectangulares homogéneas (con una sola capa), es conocido que la relación entre la energía elástica derivada de una distribución constante y la energía de una distribución parabólica (como realmente sucede en 3D) es 5/6. Sin embargo, en el caso de un compuesto laminado tal como el CLT, la derivación de los factores de corrección no es tan sencilla y depende de los espesores y rigidez de las láminas. Por lo general, para un laminado con láminas transversalmente isótropas puede asumirse que las componentes de rigidez son
Actualmente no existe pleno consenso de cómo determinar los factores de corrección Kx y Ky para el caso de platos 2D. Algunos autores, proponen emplear directamente la inversa de los factores de modificación de rigidez cortante de Timoshenko de la viga flexible, presentados en la Sección 1.2.2 correspondientes a cada una de las direcciones del plano tal que
Por otra parte, la metodología propuesta en el software RFEM Laminate, (quizá el software mayormente usado para el cálculo de elementos 2D de CLT) se describe a continuación. Las componentes de rigidez se determinan como el máximo de los siguientes 2 valores
donde
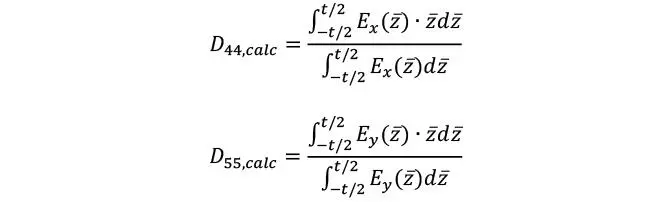
siendo Ex e Ey los módulos elásticos longitudinales de cada una de las capas en las direcciones x e y. Por otra parte, los factores D44,,min e D55.min se calculan como
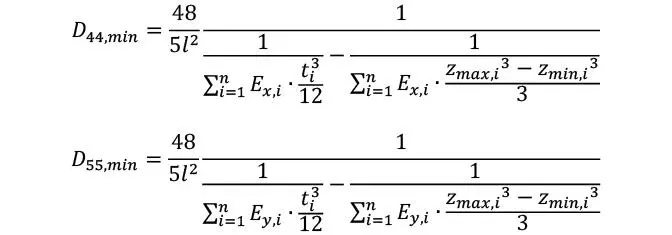
Donde l es el ancho medio del contorno rectangular que encierra la placa de CLT considerada. Los valores D44,,min y D55.min permiten incrementar la rigidez en el caso de que la placa de CLT sea muy estrecha (ya que el Dmin se incrementa notablemente al disminuir l). Este incremento de la rigidez puede ser necesario en secciones del CLT donde el ancho de la placa sea muy reducido, ya que en esos casos la tensión de corte transversal puede ser muy elevada. Además de esta corrección, el software permite aplicar un coeficiente adicional de corrección de corte.
1.3.11 Cálculo de tensiones en cada lámina
Una vez definida la matriz de rigidez y relación de vectores de deformación, el cálculo de tensiones en cada una de las láminas es sencillo. Tal como ya se introdujo en la Sección 6.1.5.5, las deformaciones globales de la placa se obtienen a partir de los esfuerzos y la matriz global de rigidez (en los casos desacoplados) como

En forma compacta
Y tal como se presentó en la Sección 1.3.3, εplaca permite determinar εlámina sin más que considerar la analogía por desplazamientos
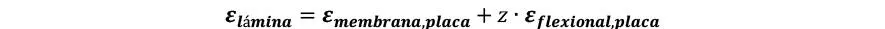
De tal modo, las tensiones en el interior de cada lámina se obtienen lógicamente considerando las deformaciones de la lámina y la rigidez de la misma
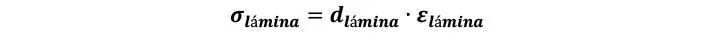
con
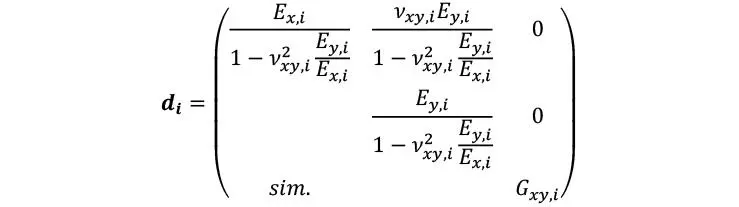
Lo que permite determinar las componentes tensionales membranales en cada lámina
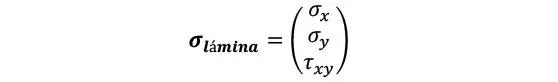
Por otro lado, las tensiones debidas al cortante transversal suelen considerarse aparte; es decir, no se calculan a partir de las deformaciones globales de la placa. En este punto es bastante habitual aproximar la tensión máxima asumiendo distribución parabólica a partir del corte unitario como
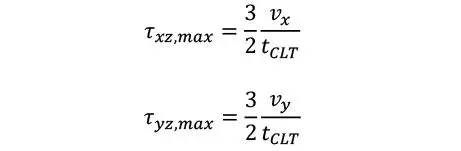
Alternativamente, pueden aplicarse procedimientos analíticos tal como los que se describieron en apartados anteriores, o procedimientos numéricos más sofisticados.
1.3.12 Verificaciones en cada lámina
Una vez determinadas las componentes de tensión membranal y corte transversal de cada lámina, es posible determinar las tensiones relevantes para las verificaciones a partir del ángulo β entre la dirección x considerada y la orientación de la fibra de cada lámina, según lo indicado en la Tabla 1.3.12.1.
| TABLA 1.3.12.1 Determinación de las tensiones relevantes para las verificaciones en cada lámina, una vez determinadas las componentes de tensión membranal y de corte transversal. |
| Tensión |
Nomencl. |
Expresión |
| Tensión paralela a la fibra total(engloba efectos de flexión y axiles) |
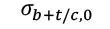 |
 |
| Tensión perpendicular a la fibra total(engloba efectos de flexión y axiles) |
|
|
| Componente tracción/compresión media paralela* |
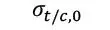 |
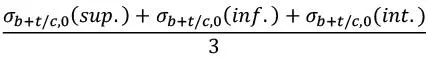 |
| Componente tracción/compresión media perpendicular* |
|
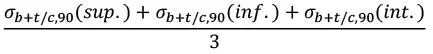 |
| Componente de flexión paralela únicamente |
|
|
| Componente de flexión perpendicular únicamente |
|
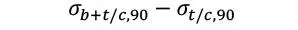 |
| Tensión de rodadura en la sección transversal perpendicular a los tablones de la lámina |
|
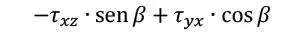 |
| Tensión de corte longitudinal en la sección transversal paralela a los tablones de la lámina |
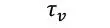 |
|
| Tensión de corte en el plano de la lámina |
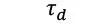 |
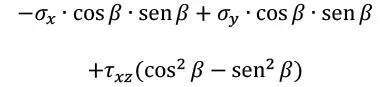 |
| * sup., inf. e int. designan, respectivamente las tensiones en la parte superior, intermedia e inferior de la lámina considerada, respectivamente. Es decir, la tensión axial media se considera como la media de las tensiones totales en cada uno de esos puntos. |
Esto permite realizar las verificaciones correspondientes, según se indica en la Tabla 1.3.12.2. Como se observa en la tabla, muchas de las típicas verificaciones se comparan directamente con la resistencia correspondiente; sin embargo, algunas tensiones interaccionan por la que se pueden emplear criterios de combinación lineales o cuadráticos.
Читать дальше