Carlos Alberto Nader - Arquitectura alternativa sostenible

En el grupo de los poliedros no convexos, los sólidos cuasirregulares son el dodecadodecaedro (m = 5, n = 5/2), cuyas aristas forman hexágonos (ecuadores o sistemas de grandes círculos), y el gran icosidodecaedro (m = 3, n = 5/2), cuyas aristas forman polígonos 10/3; se derivan de los Kepler-Poinsot y sus puntos medios de arista, y sus duales son zonoedros no convexos, se denotan (m, n, m, n, m, n).

Hay también otros poliedros no convexos cuasirregulares que no forman ecuadores de aristas: el pequeño icosidodecaedro triámbico (m = 3 y n = 5/2); el dodecadodecaedro triámbico (m = 5/3 y n = 5), y el gran icosidodecaedro triámbico (m = 3 y n = 5). Sus duales tienen caras hexagonales y son zonoedros generales, tienen los mismos vértices y aristas que el compuesto de 5 cubos (figuras 28-30).

FIGURA 28. COMPUESTO TETRAEDRO-TETRAEDRO, EN EL INTERIOR OCTAEDRO

Fuente: reinterpretada por Lina Pérez, a partir de Hart (1996b).

FIGURA 29. DODECADODECAEDRO, GRAN ICOSIDODECAEDRO

Fuente: Maeder (1995a).

FIGURA 30. PEQUEÑO ICOSIDODECAEDRO TRIÁMBICO

Fuente: Maeder (1995a).

2.2.2. Poliedros convexos uniformes

2.2.2.1. Sólidos platónicos

Son cinco sólidos regulares que se descubrieron hace más de dos mil años. Se identifican usando (p, q), donde p es el número de lados del polígono y q el número de polígonos en cada vértice. Son aquellos cuyas caras deben ser polígonos idénticos y deben encontrarse el mismo número de ellos en cada vértice, es decir, caras idénticas y vértices idénticos. A continuación, se muestran (figuras 31-35), los cinco sólidos platónicos y algunas de sus características.

·Tetraedro: 4 (3) caras, 6 aristas y 4 vértices (figura 31).

FIGURA 31. TETRAEDRO

Fuente: Maeder (1995a).

·Octaedro: 8 (3) caras, 12 aristas y 6 vértices (figura 32).

FIGURA 32. OCTAEDRO

Fuente: Maeder (1995a).

·Icosaedro: 20 (3) caras, 30 aristas y 12 vértices (figura 33).

FIGURA 33. COSAEDRO

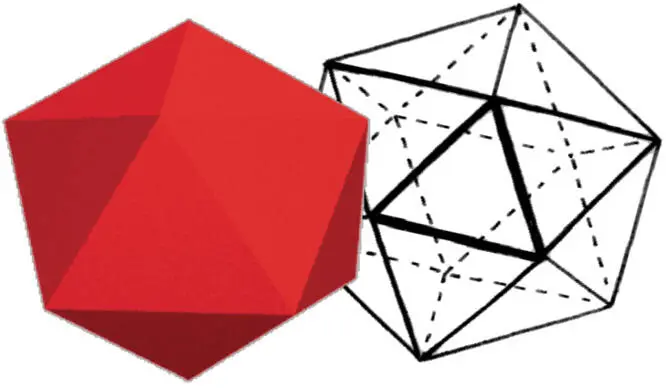
Fuente: Maeder (1995a).

·Hexaedro o cubo: 6 (4) caras, 12 aristas y 8 vértices (figura 34).

FIGURA 34. HEXAEDRO O CUBO

Fuente: Maeder (1995a).

·Dodecaedro pentagonal: 12 (5) caras, 30 aristas y 20 vértices (figura 35).

FIGURA 35. DODECAEDRO PENTAGONAL

Fuente: Maeder (1995a).

2.2.2.2. Sólidos arquimédicos

Son trece sólidos semirregulares, descubiertos por Arquímedes y posteriormente redescubiertos en el Renacimiento, hasta que Kepler finalmente los completó y clasificó en 1619. Están compuestos por polígonos regulares convexos, no necesariamente del mismo tipo y con vértices idénticos; por eso, se llaman semirregulares. Los polígonos deben aparecer en la misma secuencia, y surgen a partir de las variaciones geométricas hechas a los sólidos platónicos; la mayoría son truncaciones de estos últimos. Para la denotación de estos poliedros se escribe la composición poligonal de un vértice del poliedro en orden cíclico:

·(3, 6, 6) tetraedro truncado: 4 caras triangulares, 4 caras hexagonales, 12 vértices y 18 aristas. Derivado de la truncación del tetraedro (figura 36).

FIGURA 36. TETRAEDRO TRUNCADO

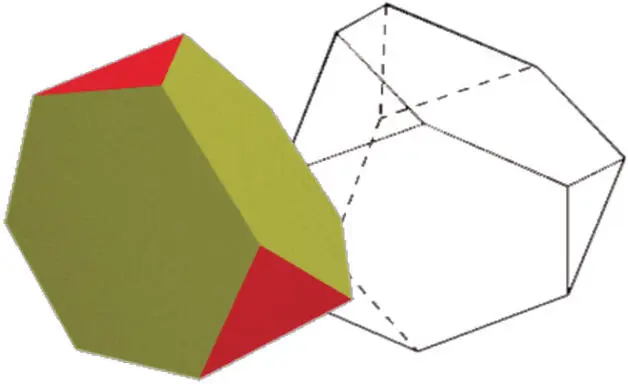
Fuente: Maeder (1995a).

·(3, 8, 8) cubo truncado: 8 caras triangulares, 6 caras octagonales, 24 vértices y 36 aristas. Derivado de la truncación de un cubo (figura 37).

FIGURA 37. CUBO TRUNCADO

Fuente: Maeder (1995a).

·(4, 6, 6) octaedro truncado: 6 caras cuadradas, 8 caras hexagonales, 24 vértices y 36 aristas. Derivado de la truncación de un octaedro (figura 38).

FIGURA 38. OCTAEDRO TRUNCADO

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.