Carlos Alberto Nader - Arquitectura alternativa sostenible

·Desarrollo de una nueva ética frente a la producción y el consumo.

Al intentar crear una arquitectura sinergética, sostenible y adaptable, necesariamente tendremos que remitirnos a la geometría espacial y sinergética. En la arquitectura tradicional, la geometría es una herramienta del diseño; sin embargo, es escaso el estudio de la estructura de la forma y sus relaciones con otras formas. Es decir, primero se diseña y luego se inventa una estructura a las formas ya dibujadas. Aquí el objetivo es entender que cualquier objeto en el espacio tiene una estructura determinada por un patrón de integridad, que es el que permite la estabilidad en dicha forma, como sucede en las corazas de proteínas que protegen a ciertos virus, lo que se observa en la figura 7. De esta manera, la geometría pasa de ser una simple lista de figuras a efectos de escoger alguna para un diseño, a ser una herramienta mucho más compleja e interesante.

En busca de un óptimo manejo espacial y estructural es necesario estudiar la geometría espacial y sus transformaciones, así como los principios de la geometría sinergética de Buckminster Fuller, en aras de comprender el comportamiento de los sistemas espaciales.

FIGURA 7. CORAZAS DE PROTEÍNAS QUE PROTEGEN LOS VIRUS

Fuente: reinterpretada por Lina Pérez.

2.1. Antecedentes

La geometría espacial ha sido objeto de estudio y fascinación desde hace muchos siglos. Por ejemplo, algunas de las piedras neolíticas que datan del año 2000 a. C., halladas en Escocia, corresponden a poliedros regulares cuyos nudos varían de 3 a 160 (figura 8).

FIGURA 8. PIEDRAS ESCOCESAS

Fuente: reinterpretada por Lina Pérez a partir de Colombo (2011).

Asimismo, diversos pensadores desde la Antigüedad han abordado este tema:

Platón. En su obra Timeo (Timaeus) describe la construcción matemática de los elementos (tierra, fuego, aire y agua) y su relación con el cubo, el tetraedro, el octaedro y el icosaedro respectivamente; el quinto sólido platónico, el dodecaedro, es el modelo, según Platón, de todo el universo. Los dodecaedros romanos son huecos, hechos en bronce, que datan del II al IV siglo a. C. (figura 9), los cuales son sólidos platónicos.

FIGURA 9. ICOSAEDRO Y DODECAEDRO ROMANOS

Fuente: Guañoc (2014).

Arquímedes. En sus tratados sobre catóptrica describe los trece poliedros semirregulares (construidos con polígonos regulares, de caras no necesariamente iguales que pueden ser inscritos en una circunferencia), hoy llamados sólidos arquimédicos. Describió también, en su libro Elementos, las relaciones entre sólidos platónicos.

Paolo Uccello. Trabajó, en el siglo XV la geometría y los poliedros, adelantándose a Kepler con las estelaciones dodecaedrales (figura 10).

FIGURA 10. INTARSIA DE UCCELLO

Fuente: Hart (1996a).

Piero della Francesca. Desarrolló nuevos métodos para hacer estudios de perspectiva, esto en el siglo XV, y redescubrió gradualmente los sólidos arquimédicos, los cuales eran desconocidos en su tiempo, y estableció relaciones entre estos y los sólidos platónicos (figura 11).

FIGURA 11. ICOSAEDRO INSCRITO EN CUBO

Fuente: Eternauta (2004).

Leonardo da Vinci (1452-1519). También desarrolló trabajos sobre los poliedros, los cuales aplicó en sus diversos modelos de artefactos y en estudios en torno a las artes plásticas; acerca de ello se hace alusión en el documento De divina proportione, escrito por Luca Pacioli a principios del siglo XVI, en el que trató temas de geometría e incluyó, originalmente, ilustraciones del propio Da Vinci (figura 12). El mismo Luca Pacioli redescubrió el rombicuboctaedro (figura 13), desconocido en su tiempo, y lo incluyó también en De devina proportione.

FIGURA 12. POLIEDROS DE CARAS VACÍAS Y LLENAS

Fuente: Rocha (2005).

FIGURA 13. ROMBICUBOCTAEDRO DE CARAS VACÍAS

Fuente: Kairnz (2010).

Daniel Barbaro. En su libro La práctica della perspectiva incluye el primer dibujo publicado de un icosidodecaedro truncado y de un rombicosidodecaedro (figura 14); esto lo desarrolló durante el siglo XVI.

FIGURA 14. ICOSIDODECAEDRO TRUNCADO Y ROMBICOSIDODECAEDRO

Fuente: Hart (1998a).

Alberto Durero. En su libro Manual del pintor, escrito a principios del siglo XVI, presentó un estudio sobre los poliedros platónicos y arquimédicos, y algunos de su propia invención, así como la influencia que estos tienen en las representaciones bidimensionales y los utiliza para estudios en torno a la perspectiva y la comprensión espacial o tridimensional sobre planos bidimensionales (figura 15).

FIGURA 15. DESARROLLO POLIÉDRICO

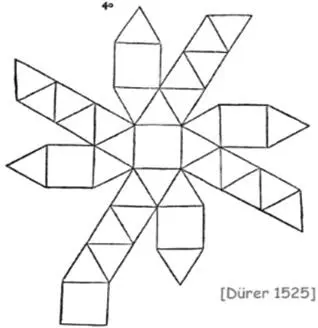
Fuente: Bortolossi (2009).

Wentzel Jamnitzer. Se anticipó cinco años a Kepler, mostrando un tricontaedro rómbico y un dodecaedro estelado, los cuales incluyó en sus publicaciones y los utilizó en sus joyas y troqueles de sellos oficiales en Alemania y Austria en el siglo XVI (figura 16).

FIGURA 16. TRICONTAEDRO RÓMBICO Y DOCECAEDRO ESTELADO

Fuente: Ibáñez (2008).

Johannes Kepler. Matemático y astrónomo, sistematizó y extendió lo que se conocía en su tiempo sobre poliedros. A principios del siglo XVII hizo una aproximación matemática a la construcción de poliedros; definió sus clases o familias de estos; descubrió otros tantos que incluyó en cada una de ellas y así las delimitó, concluyendo que no se podían construir más poliedros en cada familia de acuerdo con las características de estos, es decir, completó las familias de poliedros. También descubrió los infinitos antiprismas (figura 17).

FIGURA 17. DIBUJOS DE KEPLER

Fuente: reinterpretada por Lina Pérez a partir de Hart (1998b).