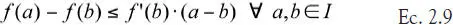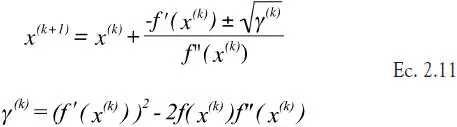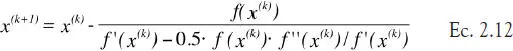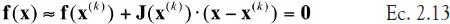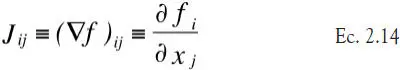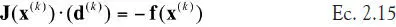Héctor Jorquera González - Métodos numéricos aplicados a Ingeniería

ii) f(x (0)) f(x (1)) < 0 y la secuencia {x (k)} converge monótonamente a x*

iii) x (1) 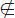I (si I = R esta opción no es válida)

Corolario 1:La condición de convexidad se puede cambiar a una de concavidad:

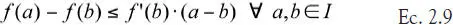
Y el teorema sigue siendo válido.

Corolario 2:En vez de condiciones de convexidad o concavidad, se puede utilizar la condición: f” (x) ≠ 0 y es continua ∀ x ∈ I.

2.3.2 Interpolación cuadrática

Dados los problemas del método de Newton clásico cuando la derivada cambia de signo y la iteración se torna inestable, se han propuesto esquemas para evitar dividir por la derivada f’(x).

En la metodología de interpolación cuadrática se aproxima f(x) en torno a x = x (k)con un polinomio de segundo orden:

y x (k+1)se obtiene haciendo P(x (k+1)) = 0:

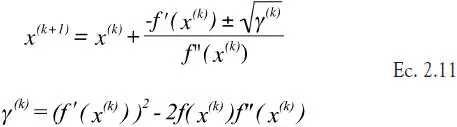
Puesto que se supone que x (k+1)≈ x (k), se escoge la raíz con menor valor absoluto en la fórmula de iteración.

Comentarios:

i) La cancelación de términos de similar valor absoluto, pero distinto signo, puede conducir a pérdida de cifras significativas en la aritmética.

ii) Dado que no se puede garantizar en general que el discriminante γ (k)en la ecuación 2.11 sea positivo, lo que se hace es remplazar uno de los factores (x-x (k)) por la expresión del método de Newton clásico 2.7, con lo que se obtiene el método de Newton extendido:

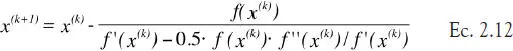
El siguiente ejemplo muestra que este método permite reducir las oscilaciones que ocurren con el método de Newton clásico, aunque no se puede concluir que el algoritmo 2.12 sea siempre robusto con respecto al estimador inicial x (1).

Ejemplo 2.5. Comparación del método de Newton clásico y su versión extendida

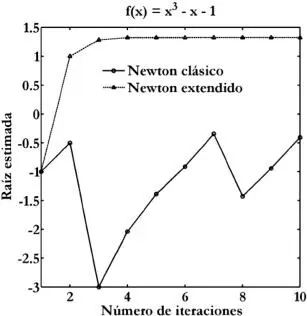
Compare el desempeño del método de Newton clásico con su variante extendida para el caso de f(x) = x 3-x-1 partiendo con x (1)= -1.

Se obtiene la siguiente figura, donde se aprecia que el método clásico oscila en las primeras 10 iteraciones sin acercarse a la raíz correcta, mientras que al método extendido le toma solamente 4 o 5 iteraciones llegar a la raíz correcta, aun cuando la derivada cerca de x (1)= -1 va cambiando de signo.

FIGURA 2.5. Desempeño de la iteración de Newton clásica y extendida

A continuación se presenta el código de Matlab ®que permite hacer los cálculos y la figura anterior.

% macro que resuelve el ejemplo 2.4

f=@(x) x^3-x-1;

fp=@(x) 3*x^2-1;

fpp=@(x) 6*x;

% secuencia iterativa del método de Newton y de su variante cuadrática

xN=zeros(10,1);

fN=zeros(10,1);

xN(1)=-1;

fN(1)=f(xN(1));

xC=zeros(10,1);

fC=zeros(10,1);

xC(1)=-1;

fC(1)=f(xC(1));

for i=2:10,

% iteración del método de Newton

xN(i)=xN(i-1)-fN(i-1)/fp(xN(i-1));

fN(i)=f(xN(i));

% iteración por método de Newton extendido

der=fp(xC(i-1));

xC(i)=xC(i-1)-fC(i-1)/(der-0.5*fC(i-1)*fpp(xC(i-1))/der);

fC(i)=f(xC(i));

end

% gráfico de comparación de resultados

plot(1:10,xN,’k-o’,1:10,xC,’k--^’);

axis square;

title(‘f(x) = x^3 - x - 1’);

xlabel(‘Número de iteraciones’);

ylabel(‘Raíz estimada’);

legend(‘Newton clásico’,’Newton extendido’);

dc(3) = k2*c(2);

2.3.3 Rutinas implementadas en Matlab ®para ecuaciones escalares

En Matlab ®, tenemos disponible como rutina de propósito general la rutina fzero . Esta rutina es híbrida, ya que combina varias técnicas en forma heurística para lograr convergencia. La rutina decide si realiza una bisección, el método de la secante o una interpolación cuadrática inversa, dependiendo de las condiciones locales. Se recomienda practicar su uso empleando la rutina fzerogui desarrollada por Moler [1]. Esta función está limitada solamente al caso de funciones continuas y no es capaz de hallar raíces donde la función no cruza el eje cambiando de signo, como es el caso de x 2en x = 0.

Para el caso particular de los polinomios, Matlab ®tiene la función roots que calcula todas las raíces. En caso de que se quiera hacer cero una ecuación cuando hay datos reales, con errores de medición, se puede plantear el problema original 2.1 como la minimización de (f) 2y aplicar entonces la función de minimización escalar fminbnd .

2.4 Sistemas de ecuaciones: el método de Newton y sus variantes

La naturaleza vectorial de un sistema de ecuaciones, en contraste con el carácter escalar de las ecuaciones en una incógnita vistas anteriormente, no modifica mucho la manera en que se resuelve iterativamente el problema. No obstante, veremos algunos detalles que se deben considerar en el momento de implementar los distintos algoritmos.

Ya hemos visto que el método de Newton corresponde a una interpolación lineal local (porque la serie de Taylor de f(x) era local). De modo análogo procedemos para los sistemas de ecuaciones: aproximamos

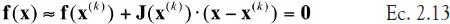
Donde el gradiente, o jacobiano J, de fviene dado por

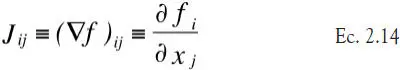
Por lo tanto, para obtener el nuevo valor x (k+1)tenemos que resolver el sistema lineal

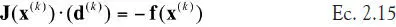
Para la corrección d (k)= x (k+1)- x (k). Este es el método de Newton para n variables. Nótese que es necesario que la inversa del jacobiano exista (no debe haber singularidad). La siguiente tabla muestra el algoritmo estándar del método en n variables.

TABLA 2.2. Algoritmo típico del método de Newton

2.4.1 Variaciones del método de Newton

En la ecuación 2.15, J (k)tiene que ser evaluado en cada iteración a partir de expresiones para las derivadas parciales. Para sistemas con muchas ecuaciones, esto no es práctico. Existen varias alternativas para reducir la cantidad de trabajo o simplificar la técnica de solución.