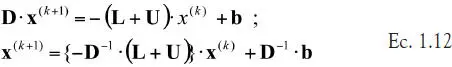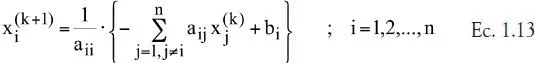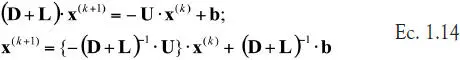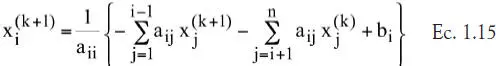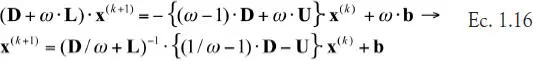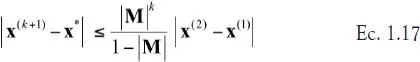Héctor Jorquera González - Métodos numéricos aplicados a Ingeniería

1.2.1 Método de Jacobi (Desplazamientos simultáneos)

En este método se aplica la descomposición 1.11 y se deja la diagonal de la matriz original en el lado izquierdo de la ecuación original, de modo que

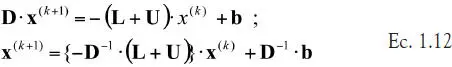
Por lo tanto, en cada iteración se calculan los nuevos componentes del vector de solución, usando la información de los componentes de la etapa anterior, por lo que en la ecuación 1.12 el componente ‘i’ del vector solución actualizado queda como:

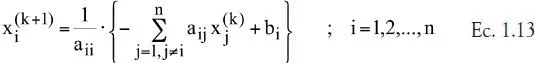
1.2.2 Método de Gauss-Seidel (Desplazamientos sucesivos)

En esta variante se pasa solo la diagonal superior de la matriz Aal lado derecho de la ecuación original, obteniéndose:

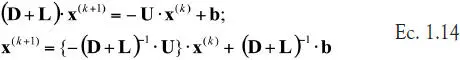
En este método, la componente i-ésima del vector solución en la etapa (k+1) se actualiza usando la información de los componentes del vector x (k)y los nuevos componentes del vector x (k+1)hasta el componente i-1:

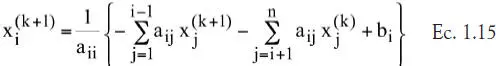
Es decir, se emplea información más actualizada que en el caso del método de Jacobi.

1.2.3 Método de relajaciones sucesivas

La mayor velocidad de convergencia del método de Gauss-Seidel (con respecto al método de Jacobi) se debe a que actualiza toda la información disponible del vector x (k+1)para calcular los restantes componentes de dicho vector, y esto se efectúa al incluir el componente Lde la matriz original Aen el lado izquierdo de la ecuación 1.14.

En el método de relajaciones sucesivas se considera la posibilidad de acelerar la convergencia de la iteración de Gauss-Seidel usando un parámetro de relajación ω, de manera que se hace una actualización de la iteración de la forma

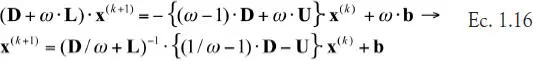
El parámetro ω es mayor que 0 y menor que 2. Si ω es mayor que 1.0, hablamos de sobrerrelajación, mientras que si 0 < ω < 1, el método se denomina subrelajación. Existen técnicas para estimar el valor óptimo del parámetro ω para una situación dada (Axelson, [4]), incluso modificando su valor a lo largo de la iteración (esquemas adaptivos), que básicamente consisten en minimizar el radio espectral (ρ) de la matriz M= ( D/ω+ L) -1·((1/ω−1)· D- U) que aparece en la ecuación anterior.

Notas

1) Los métodos de Jacobi y de Gauss-Seidel son útiles solamente cuando la matriz es diagonal dominante, lo cual garantiza la convergencia de ambos métodos.

2) Usualmente se tiene, en orden creciente de rapidez de convergencia que: Jacobi < Gauss-Seidel < Relajaciones, ya que en este último caso se puede escoger ω para minimizar ρ( M).

3) Se puede demostrar que si 0 < ω < 2 y Aes definida positiva, el método de relajaciones sucesivas converge (Sewell, [7]).

4) Se puede demostrar que si 0 < ω < 1 y Aes diagonal dominante, el método de relajaciones sucesivas converge (Sewell, [7]).

Ejemplo 1.4. Comparación de métodos iterativos

Para los siguientes sistemas de ecuaciones lineales, calcule el número de iteraciones necesarias para conseguir un valor menor a 10 -5en la norma del residuo r (k)= A· x (k) -busando los siguientes métodos: i) Jacobi; ii) Gauss-Seidel; iii) relajaciones aplicadas a Gauss-Seidel, escogiendo ω de forma de minimizar ρ( M) en el método de Gauss-Seidel.

Aplicando los distintos esquemas iterativos se obtienen los siguientes resultados:

TABLA 1.1. Resultados del ejemplo 1.4

* Calculado usando el valor óptimo de ω que minimiza ρ (M) en 1.16.

Nótese que el caso b) no converge porque la matriz no es diagonal dominante ni tampoco se puede reordenar las filas para que lo sea. Para los casos a) y c), ambas matrices poseen diagonal dominante, pero solo c) es definida positiva (todos sus valores propios son estrictamente positivos), de ahí que el método de relajaciones alcance su mayor eficacia de implementación.

Por lo tanto, una conclusión relevante es que todos los métodos iterativos de la forma general 1.9 deben pasar por un chequeo previo de que las condiciones de convergencia se cumplen, antes de intentar resolverlos por cualquier método iterativo.

A continuación presentamos un listado con el código Matlab ®de resolución iterativa mediante el método de Jacobi. El lector puede modificar fácilmente el código para implementar el método de Gauss-Seidel o el de relajaciones sucesivas.

% función que resuelve A*x=b según método de Jacobi

function [X,it,err]=Jacobi(A,b,tol,maxit)

if nargin<4,

maxit=100;

end

if nargin <3,

tol=1e-5;

end

D=diag(diag(A));

L=tril(A,-1);

U=triu(A,1);

M=-inv(D)*(L+U);

% chequeo que los valores propios cumplen la condición de convergencia

l=max(abs(eig(M)));

if l>= 1.0,

error(‘Matriz de iteración no garantiza convergencia’);

end

g=D\b;

X=zeros(size(b));

it=0;

err=norm(b);

while err > tol && it < maxit,

X=M*X+g;

err=norm(A*X-b);

it=it+1;

end

1.2.5 Estimación del error en métodos iterativos

Sea x*la solución de la ecuación genérica 1.9; se puede demostrar que una cota del error después de la k-ésima etapa de iteración viene dado por:

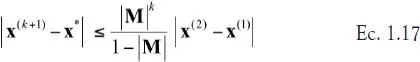
Por lo tanto, para que el método presente convergencia, es necesario que la norma de la matriz Msea menor que 1.0. Esto es equivalente a exigir que el radio espectral de la matriz M, definido en la ecuación 1.10, sea menor que 1.0.

No obstante lo anterior, si la norma de la matriz Mes mayor que 1.0, es posible resolver la ecuación 1.7 de manera indirecta usando los residuos r (j)de dicha iteración, a través de métodos del gradiente conjugado (Axelsson, [4]; Sewell, [7]), los cuales son más complejos de implementar y cuyo desempeño depende fuertemente de la estructura del espectro de valores propios de la matriz M, por lo que no es fácil predecir su desempeño.

Cuando tengamos que resolver en forma iterativa un caso como el recién descrito, habría que probar con los métodos iterativos que trae Matlab ®y que se describen en la siguiente sección.