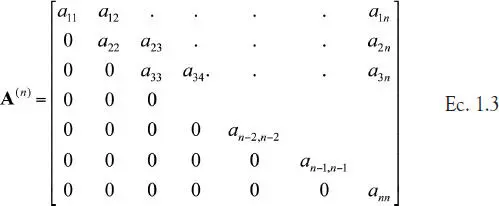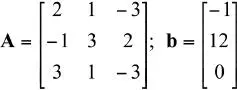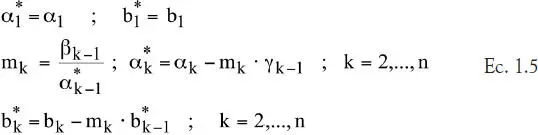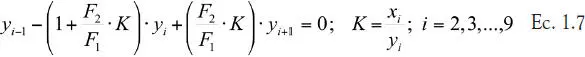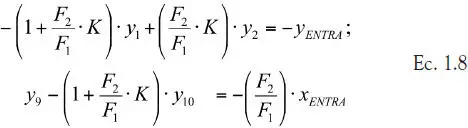Héctor Jorquera González - Métodos numéricos aplicados a Ingeniería

1.1 Métodos de solución directa

Un método directo es un algoritmo con un número finito y predefinido de pasos, al final de los cuales se obtiene la solución.

1.1.1 Eliminación de Gauss-Jordan

Este algoritmo consiste en producir una serie de transformaciones del sistema lineal original, hasta obtener un sistema triangular superior. Supongamos que nuestro punto de partida consiste en el sistema de ecuaciones lineales

Se genera una secuencia de operaciones hasta que se transforma el sistema original de ecuaciones a un sistema con matriz triangular superior U:

La solución de esta ecuación es la misma que la de la ecuación 1.1.

Para conseguir la estructura triangular superior se procede a eliminar los elementos bajo la diagonal principal, haciéndolos cero a través de operaciones (sumas y restas) con las filas de la matriz A. Al final del procesamiento se obtiene la siguiente estructura de matriz:

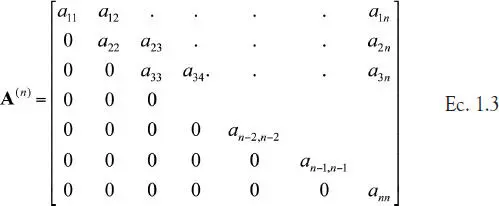
Esto genera el sistema de ecuaciones U · x = y, el cual se puede resolver por sustitución hacia atrás para obtener la solución x.

Ejemplo 1.1. Eliminación de Gauss-Jordan

Utilice Matlab ®para realizar la eliminación de Gauss-Jordan del siguiente sistema de ecuaciones A · x = b,

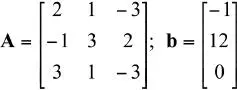
Solución:Se hace el pivoteo de la matriz Aen conjunto con el vector b, de manera de producir directamente el resultado mostrado en la ecuación 1.2; para esto se opera con una matriz aumentada M = [A b]. El siguiente macro de Matlab ®resuelve el problema propuesto:

% este macro resuelve el Ejemplo 1.1

%% ingreso de la matriz y vector lado derecho

A=[2 1 -3; -1 3 2; 3 1 -3];

b=[-1 12 0]’;

x=zeros(size(b));

%% definición matriz aumentada M y eliminación Gauss-Jordan

M=[A b];

M(1,:)=M(1,:)/M(1,1); % se normaliza fila 1 con primer pivote

M(2,:)=M(2,:)-M(1,:)*M(2,1); % se genera un ‘0’ en posición (2,1)

M(3,:)=M(3,:)-M(1,:)*M(3,1); % se genera un ‘0’ en posición (3,1)

M(2,:)=M(2,:)/M(2,2); % se normaliza fila 2 con segundo pivote

M(3,:)=M(3,:)-M(2,:)*M(3,2); % se genera un ‘0’ en posición (3,2)

%% etapa de solución de la ecuación por sustitución hacia atrás

x(3)=M(3,4)/M(3,3);

x(2)=M(2,4)-M(2,3)*x(3);

x(1)=M(1,4)-M(1,3)*x(3)-M(1,2)*x(2);

%% verificación de la solución

r=A*x-b;

El resultado de aplicar este macro es:

Notas

1) El método como aquí se ha descrito (eliminación de Gauss-Jordan) falla si cualquiera de los pivotes (elementos de la diagonal de la matriz A) se hace cero o si es muy pequeño por causa de errores de redondeo; por ejemplo, resta de cantidades de similar magnitud.

2) En la práctica es necesario usar una estrategia de pivoteo para escoger el “mejor” pivote, de manera de minimizar los problemas numéricos. El mejor pivote es usualmente el elemento con mayor valor absoluto en la columna que queda bajo la diagonal principal durante la eliminación hacia adelante.

3) En Matlab ®, el algoritmo está implementado como la factorización LU (rutina lu ), y también en el operador ‘\’, que usa la eliminación gaussiana para resolver sistemas lineales. Moler [1] ha desarrollado una interfaz gráfica lugui que permite visualizar el proceso de factorización de una matriz cuadrada, para distintas opciones: sin pivote, pivoteo parcial o pivoteo total.

4) En el caso particular de matrices que sean definidas positivas o que posean diagonal dominante 1, el pivoteo siempre funciona y no hay problemas de encontrar pivotes iguales a cero.

1.1.2 Caso de matrices tridiagonales

Un ejemplo simple de aplicación de la eliminación de Gauss-Jordan es el caso de una matriz tridiagonal, de la forma

Si se cumple la condición de diagonal dominante para la matriz: |α i| > |γ i| + |β i-1|, (para todo i), entonces el proceso de eliminación de Gauss-Jordan queda dado por el algoritmo de Thomas:

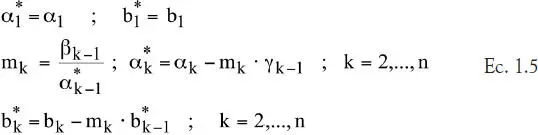
Y la etapa de sustitución hacia atrás queda como

Notas

1) Este algoritmo no solo evita operaciones aritméticas innecesarias con elementos nulos de la matriz, sino que asimismo reduce la cantidad de almacenamiento requerido de O(n 2) a O(5·n) aproximadamente, ya que almacena la matriz Acomo tres vectores α, β y γ. Este algoritmo está disponible en la rutina tridisolve desarrollada por Moler [1].

2) Este enfoque se puede implementar de modo eficiente cuando la matriz original posee una estructura regular. Esta matriz tridiagonal aparece frecuentemente cuando se modelan balances de masa en procesos de separación, tales como destilación (Wang y Henke, [2]), absorción, extracción por solventes (Hanna y Sandall, [3]); igualmente aparece en problemas de contorno (ecuaciones diferenciales ordinarias o a derivadas parciales) cuando se usan métodos de diferencias finitas (capítulos 4 y 5).

Ejemplo 1.2. Solución de un sistema tridiagonal

Se remueve anilina desde una corriente acuosa usando tolueno como solvente extractor; los flujos de agua (F 1) y tolueno (F 2) son constantes (en base libre de soluto). La unidad de separación es una torre en contracorriente con 10 etapas de extracción, como se muestra en la Figura 1.1, con la siguiente notación:

x i= kg de anilina en fase orgánica/kg de tolueno en fase orgánica.

y i= kg de anilina en fase acuosa/kg de agua en fase acuosa.

FIGURA 1.1. Esquema de la extracción líquido-líquido del ejemplo 1.2

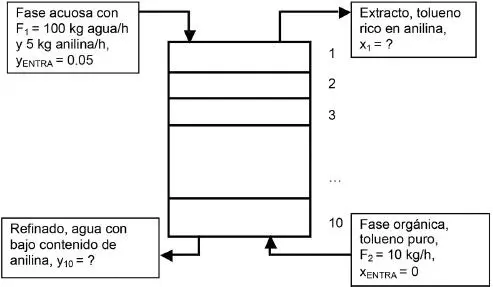
Los subíndices ‘i’ corresponden a las composiciones de las corrientes que salen de la etapa ‘i’ de extracción. Las ecuaciones del balance de masa en cada etapa ‘i’ se pueden poner como sigue:

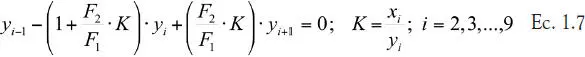
Donde K es el coeficiente de reparto de soluto entre ambas fases, supuesto constante en todas las etapas. Para las etapas 1 y 10 hay que considerar:

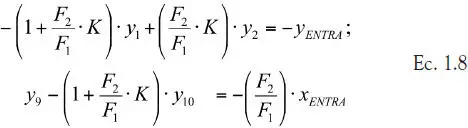
Construya un macro que resuelva este sistema de ecuaciones y que grafique las concentraciones de anilina en ambas fases, en función del número de etapas, si se considera que K = 4 = constante.